- O MMC organiza múltiplos comuns e se conecta ao MDC pela identidade MDC×MMC=|a×b|.
- Para somar/subtrair frações, use o MMC dos denominadores para obter o menor denominador comum.
- O MMC de frações a/b e c/d é MMC(a,c) ÷ MDC(b,d); o MDC é MDC(a,c) ÷ MMC(b,d).
- A fatoração em primos torna cálculos com números grandes rápidos, claros e confiáveis.
Encontrar o mínimo múltiplo comum de duas frações pode parecer diferente do que fazemos com números inteiros, mas segue ideias muito próximas e, quando bem entendido, vira uma ferramenta poderosa para resolver problemas com racionalidade. Neste guia, você vai aprender quando usar o MMC entre denominadores para somar e subtrair frações, como calcular o MMC de frações propriamente dito e como tirar proveito da fatoração em primos para lidar com números grandes sem dor de cabeça.
Além do MMC, também vamos aproveitar para amarrar as pontas com o MDC (máximo divisor comum), já que essas duas ideias caminham de mãos dadas. Você vai ver a relação clássica entre MMC e MDC, propriedades úteis, exemplos resolvidos e um problema típico de prova (como o das lâmpadas piscando) para consolidar o entendimento. Tudo em português, com linguagem direta e aquele toque coloquial que ajuda a fixar.
O que é Mínimo Múltiplo Comum (MMC)
Quando trabalhamos com dois ou mais números inteiros positivos, é possível listar seus múltiplos. O MMC é o menor número diferente de zero que aparece em todas as listas de múltiplos ao mesmo tempo, isto é, o menor múltiplo comum a todos os números considerados.
Para visualizar, considere os números 2, 8 e 10. Vamos listar alguns múltiplos iniciais de cada um: M(2) = {2, 4, 6, 8, 10, 12, 14, 16, 18, 20, …}; M(8) = {8, 16, 24, 32, 40, 48, 56, 64, 72, 80, …}; M(10) = {10, 20, 30, 40, 50, 60, 70, 80, 90, 100, …}. Repare que há diversos números em comum entre essas listas (como 40 e 80 entre 8 e 10), e o primeiro que aparece em todas as três ao mesmo tempo é o MMC de 2, 8 e 10.
Essa ideia de “múltiplos comuns” é a base do conceito. Ao identificar o menor dos múltiplos comuns, encontramos o MMC. Para números pequenos, listar é simples; para números grandes, há um atalho muito melhor (a fatoração em primos), que veremos adiante.
Como determinar o MMC na prática
Existe um método direto: listar múltiplos de cada número e achar o primeiro elemento em comum. Entre 4 e 8, por exemplo, os múltiplos são M(4) = {4, 8, 12, 16, 20, …} e M(8) = {8, 16, 24, 32, 40, …}; o menor número presente nas duas listas é 8, então MMC(4, 8) = 8.
Esse método, porém, não é prático quando os números são grandes. Pense em 2 e 121: listar M(2) até passar de 121 é pouco eficiente. Em situações assim, usamos a decomposição em fatores primos para chegar ao resultado de forma rápida e segura.
Para calcular MMC(121, 2), decompomos: 121 = 11 × 11 e 2 já é primo. O MMC deve conter todas as bases primas presentes nos números com o maior expoente visto: MMC(121, 2) = 2 × 11 × 11 = 242. Simples e limpo, sem listas gigantes.
Decomposição em fatores primos (passo a passo)
A fatoração consiste em escrever um número como produto de primos. O procedimento é: dividir pelo menor primo possível, repetir a divisão com o quociente e seguir assim até chegar ao 1. É a aplicação direta do Teorema Fundamental da Aritmética, que garante que todo número composto pode ser escrito de maneira única como produto de primos.
Exemplo simples: 40. Começando pelo 2, temos 40 ÷ 2 = 20; novamente 2: 20 ÷ 2 = 10; mais uma vez 2: 10 ÷ 2 = 5; e 5 é primo. Logo, 40 = 2 × 2 × 2 × 5 = 2^3 × 5. Essa forma fatorada facilita tanto o MMC quanto o MDC.
Agora, fatorando 40 e 60 simultaneamente, obtemos: 40 = 2^3 × 5 e 60 = 2^2 × 3 × 5. Para o MMC, tomamos cada primo com o maior expoente que aparece: 2^3, 3^1 e 5^1, resultando em MMC(40, 60) = 2^3 × 3 × 5 = 8 × 3 × 5 = 120.
Já o MDC (máximo divisor comum) vem dos menores expoentes dos primos comuns: os dois números possuem 2^2 e 5^1 em comum, então MDC(40, 60) = 2^2 × 5 = 20. Veremos mais sobre essa dupla MMC-MDC na próxima seção.
Propriedades importantes do MMC e relação com o MDC
Uma propriedade central, muito útil em provas e contas mentais, afirma: MDC(a, b) × MMC(a, b) = |a × b|. Essa igualdade conecta as duas grandezas e permite obter uma a partir da outra quando se conhece o produto dos números.
Outra propriedade fundamental é: todo múltiplo comum de dois (ou mais) números é múltiplo do MMC desses números. Em outras palavras, o conjunto de múltiplos comuns é “gerado” pelo MMC — é como se o MMC fosse a “semente” que produz todos os múltiplos comuns.
Há ainda um caso bem especial: se a e b são primos entre si (ou seja, não compartilham divisores além do 1), então MMC(a, b) = a × b. Exemplo clássico: 5 e 21. Como não têm divisores em comum, MMC(5, 21) = 5 × 21 = 105. Pela fatoração, 21 = 3 × 7, e portanto o MMC é 3 × 5 × 7 = 105, confirmando a regra.
MMC e frações: soma, subtração e o MMC de frações em si
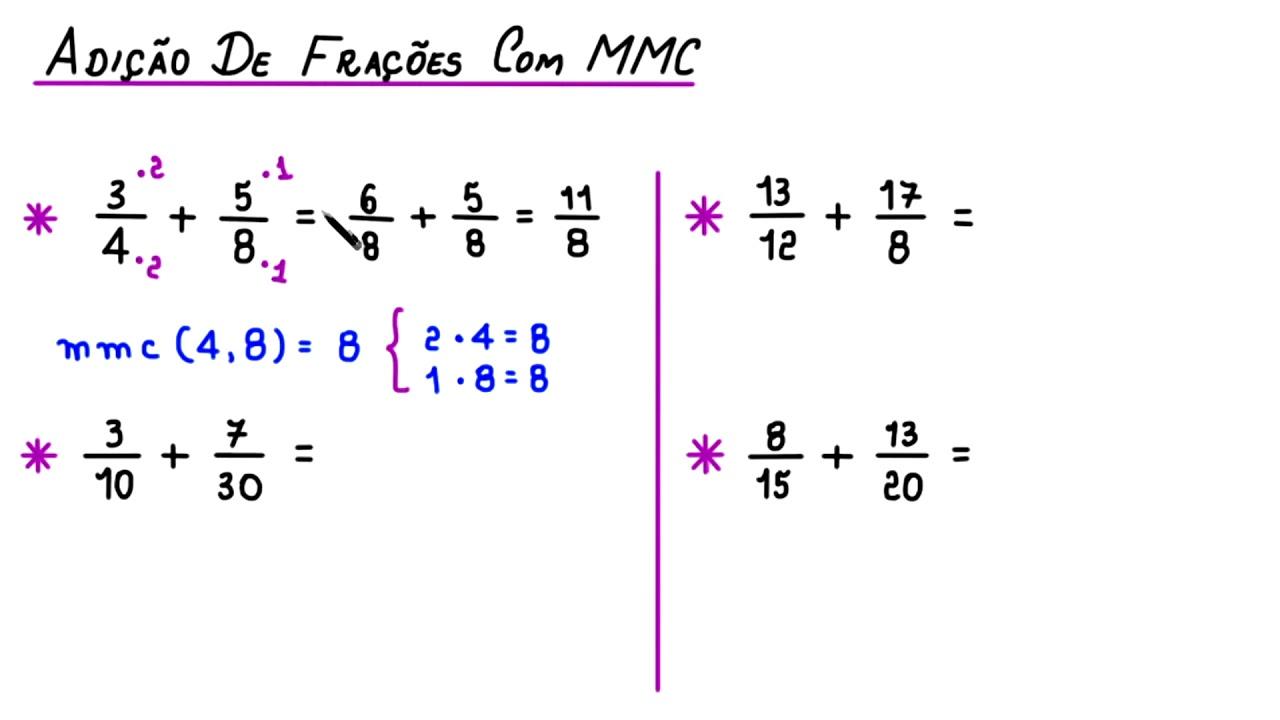
Ao somar ou subtrair frações com denominadores diferentes, usamos o MMC dos denominadores para obter o denominador comum, como em exercícios de soma racional. Esse é o denominador mais “econômico”, pois é o menor múltiplo que serve a todos os denominadores envolvidos, evitando crescer demais a fração resultante.
Por exemplo, vamos somar 4/7 e 5/3. Os denominadores são 7 e 3, que são primos entre si; logo, o MMC(7, 3) = 21. Reescrevendo: 4/7 = 12/21 e 5/3 = 35/21. Então 4/7 + 5/3 = 12/21 + 35/21 = 47/21. Para subtrair frações, a lógica é idêntica; a única diferença é a operação entre os numeradores após a equivalência para o denominador comum.
Mas e quando nos pedem o “MMC de duas frações”, não dos seus denominadores? Existe uma definição análoga à dos inteiros para números racionais. O MMC de duas frações x e y é a menor fração positiva que é múltiplo de ambas. Assim como para inteiros, vale a relação MMC(x, y) × MDC(x, y) = |x × y| também para frações positivas.
Há um atalho extremamente útil, derivado dessa relação e da forma do MDC de frações: o MMC de frações a/b e c/d é dado por MMC(a, c) ÷ MDC(b, d). Ou seja, calcule o MMC dos numeradores e divida pelo MDC dos denominadores, sempre considerando a/b e c/d como números racionais positivos (em notação padrão).
Esse resultado fica mais claro quando lembramos que o MDC de frações a/b e c/d é MDC(a, c) ÷ MMC(b, d), como enunciado na literatura de aritmética de frações. Sabendo que MMC(x, y) × MDC(x, y) = |x × y|, conseguimos deduzir a fórmula do MMC de frações apresentada acima. É um pacote coerente: MDC de frações usa MMC nos denominadores, e o MMC de frações usa MDC nos denominadores.
Vamos ilustrar. Para 4/7 e 5/3, temos MMC dos numeradores MMC(4, 5) = 20 e MDC dos denominadores MDC(7, 3) = 1. Logo, MMC(4/7, 5/3) = 20 ÷ 1 = 20. Se verificarmos via relação com o MDC de frações: MDC(4/7, 5/3) = MDC(4, 5) ÷ MMC(7, 3) = 1 ÷ 21 = 1/21; e como (4/7) × (5/3) = 20/21, então MMC = (20/21) ÷ (1/21) = 20. Tudo consistente.
Outro exemplo com denominadores que compartilham fator comum: considere 8/6 e 10/15. Temos MMC dos numeradores MMC(8, 10) = 40 e MDC dos denominadores MDC(6, 15) = 3. Portanto, MMC(8/6, 10/15) = 40 ÷ 3. Se você preferir conferir pela identidade MMC × MDC = produto, primeiro calcule o MDC de frações: MDC(8/6, 10/15) = MDC(8, 10) ÷ MMC(6, 15) = 2 ÷ 30 = 1/15; então o produto (8/6) × (10/15) = 80/90 = 8/9; finalmente, MMC = (8/9) ÷ (1/15) = (8/9) × 15 = 40/3, coincidindo com o atalho acima. Essa técnica organiza a conta e evita confusão.
Resumo deste bloco para não se perder: para “somar” ou “subtrair” frações a técnica é usar MMC dos denominadores para obter equivalências; já para “encontrar o MMC de duas frações como objetos racionais”, use MMC(a, c) ÷ MDC(b, d). E, de quebra, quando precisar do MDC de frações, recorra a MDC(a, c) ÷ MMC(b, d).
Exemplo aplicado: lâmpadas piscando (questão típica)
Problema clássico: lâmpadas amarelas acendem a cada 45 s, verdes a cada 60 s, azuis a cada 27 s, e as vermelhas só acendem quando todas as outras estão acesas ao mesmo tempo. De quanto em quanto tempo as vermelhas acendem?
Basta calcular o MMC entre 45, 60 e 27. Pelas fatorações: 45 = 3^2 × 5; 60 = 2^2 × 3 × 5; 27 = 3^3. Tomando os maiores expoentes, temos 2^2 × 3^3 × 5 = 4 × 27 × 5 = 540 segundos. Convertendo para minutos: 540 ÷ 60 = 9 min. Portanto, a resposta correta é 9 minutos.
MMC e MDC simultaneamente pela fatoração
Em muitos exercícios práticos, vale a pena calcular MMC e MDC ao mesmo tempo usando a fatoração. O raciocínio é: MMC junta todos os primos com o maior expoente; MDC pega apenas os primos que aparecem em todos os números, com o menor expoente. Esse método é extremamente eficiente para conjuntos com dois ou três números, e escala bem com mais termos.
Vamos resolver alguns exemplos de uma vez só: 10, 20 e 30. Fatorando, 10 = 2 × 5; 20 = 2^2 × 5; 30 = 2 × 3 × 5. MMC = 2^2 × 3 × 5 = 60; e o MDC envolve os primos comuns a todos com seus menores expoentes: 2^1 × 5^1 = 10. Resultado: MMC(10, 20, 30) = 60 e MDC(10, 20, 30) = 10.
Mais um: 15, 25 e 45. Temos 15 = 3 × 5; 25 = 5^2; 45 = 3^2 × 5. MMC = 3^2 × 5^2 = 225. O MDC, por sua vez, olha o que é comum a todos (o 5) e toma o menor expoente (1): MDC = 5. Logo, MMC(15, 25, 45) = 225 e MDC(15, 25, 45) = 5.
Outro conjunto bastante comum: 40, 60 e 80. Fatorações: 40 = 2^3 × 5; 60 = 2^2 × 3 × 5; 80 = 2^4 × 5. MMC = 2^4 × 3 × 5 = 240. O MDC usa os menores expoentes dos primos comuns (2 e 5): 2^2 × 5 = 20. Assim, MMC(40, 60, 80) = 240 e MDC(40, 60, 80) = 20.
Conectando tudo: quando usar MMC de denominadores e quando o MMC de frações
Na prática do dia a dia, a maior parte das questões com frações pede o MMC dos denominadores para obter equivalência e realizar operações. É o caso de somas, subtrações e comparações de frações com denominadores distintos. Você encontra o denominador comum mínimo, ajusta os numeradores e faz a operação.
Por outro lado, algumas questões teóricas (ou de olimpíadas) perguntam pelo “MMC de duas frações” como objetos matemáticos. Nessa situação, use a fórmula MMC(a/b, c/d) = MMC(a, c) ÷ MDC(b, d). É comum também pedirem o correspondente para o MDC de frações, que fica MDC(a/b, c/d) = MDC(a, c) ÷ MMC(b, d). Ambas as expressões são consistentes com a identidade MMC × MDC = |produto| também válida para racionais positivos.
Se você se perguntar por que essas fórmulas fazem sentido, pense que, ao “limpar” fatores em numerador e denominador, o comportamento multiplicativo dos inteiros se transporta para as frações. A fatoração em primos continua sendo a bússola: ela informa como combinar potências de cada primo para formar o menor múltiplo comum (ou o maior divisor comum) no ambiente dos racionais.
Mais exemplos para fixar
Exemplo 1 (MMC de denominadores para somar): calcule 3/10 + 7/12. Fatorando denominadores: 10 = 2 × 5, 12 = 2^2 × 3. MMC(10, 12) = 2^2 × 3 × 5 = 60. Reescrevendo: 3/10 = 18/60 e 7/12 = 35/60. Soma: 18/60 + 35/60 = 53/60.
Exemplo 2 (MDC de frações e MMC de frações via fórmula): considere 6/14 e 15/20. Temos MDC dos numeradores MDC(6, 15) = 3 e MMC dos denominadores MMC(14, 20) = (2 × 7) e (2^2 × 5) ⇒ 2^2 × 5 × 7 = 140. Assim, MDC(6/14, 15/20) = 3 ÷ 140 = 3/140. Para o MMC, faça MMC dos numeradores MMC(6, 15) = 30 e MDC dos denominadores MDC(14, 20) = 2. Logo, MMC(6/14, 15/20) = 30 ÷ 2 = 15.
Exemplo 3 (MMC por fatoração com número grande): MMC(84, 121). Temos 84 = 2^2 × 3 × 7 e 121 = 11^2. Juntando maiores expoentes, MMC = 2^2 × 3 × 7 × 11^2 = 4 × 3 × 7 × 121 = 10164. Em problemas assim, a fatoração evita listas enormes e dá o resultado sem esforço desnecessário.
Erros comuns e dicas práticas
- Confundir “MMC de denominadores” com “MMC de frações”: para operações entre frações, use o MMC dos denominadores; para o MMC das frações como racionais, aplique MMC(a, c) ÷ MDC(b, d).
- Esquecer da relação com o MDC: MMC(a, b) × MDC(a, b) = |a × b| ajuda a conferir resultados e a obter uma grandeza quando a outra é mais simples de achar.
- Não fatorar quando os números são grandes: liste múltiplos apenas quando a conta for curta. Para números médios ou grandes, fatorar é o caminho mais rápido e confiável.
- Ignorar sinais em operações: em somas e, principalmente, subtrações de frações, atente ao sinal; o denominador comum não muda o cuidado com o operador entre as parcelas.
Você agora tem um mapa completo: entende o que é o MMC, domina a fatoração em primos, aplica as propriedades, soma e subtrai frações com o MMC dos denominadores e, quando necessário, calcula o MMC de duas frações de forma direta. Para treinar, vale refazer os exemplos sem olhar o gabarito e criar casos próprios (misture denominadores com e sem fatores comuns). Assim, a fluidez nas contas aparece naturalmente.
