O modelo atômico de Heisenberg, proposto pelo físico alemão Werner Heisenberg em 1927, é uma teoria quântica que descreve o comportamento dos átomos e suas partículas constituintes. Este modelo introduz o princípio da incerteza, que afirma que é impossível determinar exatamente a posição e a velocidade de uma partícula subatômica simultaneamente.
As principais características do modelo atômico de Heisenberg incluem a ideia de que os elétrons não se movem em órbitas definidas ao redor do núcleo, mas sim em regiões de probabilidade chamadas orbitais. Além disso, o modelo de Heisenberg destaca a importância da dualidade onda-partícula, que sugere que as partículas subatômicas possuem tanto propriedades de partículas quanto de ondas.
No entanto, o modelo atômico de Heisenberg possui algumas limitações, como a dificuldade em visualizar e interpretar os resultados obtidos a partir de suas equações complexas. Além disso, algumas críticas apontam que o modelo não consegue explicar completamente a estrutura atômica de elementos químicos mais complexos. Apesar dessas limitações, o modelo atômico de Heisenberg foi fundamental para o desenvolvimento da física quântica e da compreensão do comportamento dos átomos.
Entenda o princípio da incerteza de Heisenberg na física quântica.
O Modelo Atômico de Heisenberg é uma teoria fundamental da física quântica que revolucionou nossa compreensão do mundo subatômico. Desenvolvido pelo físico alemão Werner Heisenberg na década de 1920, o modelo introduziu o princípio da incerteza, que afirma que é impossível determinar simultaneamente com precisão a posição e o momento de uma partícula subatômica.
De acordo com o princípio da incerteza de Heisenberg, quanto mais precisamente medimos a posição de uma partícula, menos precisamente podemos determinar seu momento, e vice-versa. Isso significa que há um limite fundamental para o conhecimento que podemos ter sobre as propriedades de uma partícula subatômica.
Essa limitação tem implicações profundas para a física quântica e para nossa compreensão da natureza do universo. Ela sugere que o mundo subatômico é intrinsecamente incerto e imprevisível, desafiando nossa intuição sobre como as coisas funcionam no nível mais fundamental.
Apesar de suas características inovadoras, o Modelo Atômico de Heisenberg também possui limitações. Por exemplo, ele não consegue explicar completamente a natureza dual onda-partícula das partículas subatômicas, nem reconciliar-se plenamente com a teoria da relatividade de Einstein.
Em resumo, o Modelo Atômico de Heisenberg e o princípio da incerteza abriram novos horizontes na física quântica, desafiando nossas concepções tradicionais sobre a realidade. Apesar de suas limitações, essa teoria continua sendo uma das pedras angulares da física moderna, inspirando gerações de cientistas a explorar os mistérios do universo subatômico.
Características do modelo atômico quântico: o que você precisa saber.
O modelo atômico quântico, também conhecido como modelo de Heisenberg, foi proposto pelo físico alemão Werner Heisenberg em 1927. Este modelo revolucionou a física quântica ao introduzir novos conceitos e princípios que desafiaram a visão clássica do átomo.
Uma das principais características do modelo atômico quântico é a ideia de que o comportamento das partículas subatômicas, como elétrons, não pode ser previsto com precisão. Isso ocorre devido ao princípio da incerteza de Heisenberg, que afirma que é impossível determinar simultaneamente a posição e o momento de uma partícula com precisão absoluta.
Além disso, no modelo atômico quântico, os elétrons não se movem em órbitas definidas ao redor do núcleo, como no modelo de Bohr. Em vez disso, eles são descritos por distribuições de probabilidade chamadas orbitais, que representam a região onde a probabilidade de encontrar um elétron é maior.
Outra característica importante do modelo atômico quântico é a dualidade onda-partícula, que sugere que partículas subatômicas, como elétrons, podem se comportar tanto como partículas quanto como ondas. Isso significa que os elétrons podem exibir propriedades de onda, como interferência e difração, além de se comportarem como partículas ao interagir com outras partículas.
Apesar de suas contribuições significativas para a física quântica, o modelo atômico de Heisenberg também possui algumas limitações. Por exemplo, ele não consegue explicar completamente a estrutura dos átomos mais complexos, como os átomos com vários elétrons. Além disso, o modelo não fornece uma representação visual clara do átomo, tornando mais difícil para os estudantes compreenderem sua estrutura.
Em resumo, o modelo atômico quântico, ou modelo de Heisenberg, é uma teoria fundamental na física quântica que introduziu novos conceitos e princípios para descrever o comportamento dos átomos e partículas subatômicas. Apesar de suas limitações, ele continua sendo uma ferramenta essencial para os cientistas na compreensão do mundo microscópico.
A principal característica do modelo atómico de Schrödinger: a descrição probabilística dos átomos.
O modelo atómico de Schrödinger é baseado na mecânica quântica e introduz a ideia de que os átomos são descritos por funções de onda que representam a probabilidade de encontrar uma partícula em uma determinada região do espaço. Diferentemente dos modelos anteriores, que descreviam os átomos de forma determinística, o modelo de Schrödinger considera que a posição e a energia de uma partícula são incertas e podem ser descritas apenas por uma distribuição de probabilidades.
Essa abordagem probabilística permite explicar fenômenos que os modelos clássicos não conseguiam, como o comportamento dos elétrons em torno do núcleo atómico. Além disso, o modelo de Schrödinger é capaz de prever com precisão as propriedades dos átomos e das moléculas, sendo fundamental para o desenvolvimento da química quântica e da física moderna.
No entanto, o modelo atómico de Schrödinger apresenta algumas limitações, como a complexidade matemática envolvida em sua aplicação prática e a dificuldade de interpretação física das funções de onda. Apesar disso, a descrição probabilística dos átomos continua sendo uma característica fundamental do modelo de Schrödinger, permitindo uma compreensão mais profunda do mundo microscópico.
Modelo atômico de Heisenberg: características e limitações
Princípio da incerteza de Heisenberg e suas consequências na teoria atômica moderna.
O Princípio da incerteza de Heisenberg é uma das bases da física quântica e tem importantes consequências na teoria atômica moderna. Este princípio, formulado por Werner Heisenberg em 1927, afirma que é impossível determinar com precisão simultaneamente a posição e a velocidade de uma partícula subatômica. Em outras palavras, quanto mais precisamente medimos a posição de uma partícula, menos precisamente podemos medir sua velocidade, e vice-versa.
Essa incerteza fundamental tem implicações significativas no Modelo atômico de Heisenberg. No modelo tradicional de átomos, os elétrons são representados como partículas com órbitas definidas ao redor do núcleo. No entanto, de acordo com o Princípio da incerteza, não podemos saber com certeza a posição e a velocidade dos elétrons em um átomo. Isso significa que a ideia de órbitas fixas e bem definidas não se aplica mais.
No Modelo atômico de Heisenberg, os elétrons são descritos como nuvens de probabilidade que indicam a região onde é mais provável encontrar um elétron em um determinado momento. Essa abordagem probabilística representa uma mudança radical em nossa compreensão da estrutura atômica e nos leva a abandonar a ideia de um movimento preciso e determinístico das partículas subatômicas.
Em resumo, o Princípio da incerteza de Heisenberg e o Modelo atômico associado a ele nos mostram que a natureza subatômica é intrinsecamente probabilística e desafiadora de se compreender completamente. Essas ideias revolucionárias trouxeram uma nova perspectiva para a teoria atômica moderna e continuam a desafiar nossas concepções tradicionais sobre o funcionamento do mundo microscópico.
Modelo atômico de Heisenberg: características e limitações
O modelo atómico Heisenberg (1927) introduziu o princípio da incerteza nas orbitais de electrões que rodeiam o núcleo atómico. O principal físico alemão estabeleceu os fundamentos da mecânica quântica para estimar o comportamento das partículas subatômicas que compõem um átomo.
O princípio da incerteza de Werner Heisenberg indica que não é possível saber com certeza a posição ou momento linear de um elétron. O mesmo princípio se aplica às variáveis tempo e energia; isto é, se tivermos uma indicação sobre a posição do elétron, não conheceremos o momento linear do elétron e vice-versa.

Em resumo, não é possível prever simultaneamente o valor de ambas as variáveis. O exposto acima não implica que nenhuma das magnitudes mencionadas anteriormente não possa ser conhecida com precisão. Sempre que separado, não há impedimento para a obtenção do valor do interesse.
No entanto, a incerteza ocorre quando se trata de conhecer simultaneamente duas magnitudes conjugadas, como a posição e o momento linear, e o tempo juntamente com a energia.
Este princípio surge devido a um raciocínio estritamente teórico, como a única explicação viável para fundamentar as observações científicas.
Caracteristicas
Em março de 1927, Heisenberg publicou seu trabalho sobre o conteúdo perceptivo da cinemática e mecânica teórica quântica , onde detalhou o princípio da incerteza ou indeterminação.
Este princípio, fundamental no modelo atômico proposto por Heisenberg, é caracterizado pelo seguinte:
– O princípio da incerteza surge como uma explicação que complementa as novas teorias atômicas sobre o comportamento dos elétrons. Apesar de usar instrumentos de medição com alta precisão e sensibilidade, a indeterminação permanece presente em qualquer ensaio experimental.
– Devido ao princípio da incerteza, ao analisar duas variáveis relacionadas, se você tiver um conhecimento preciso de uma delas, a indeterminação sobre o valor da outra variável aumentará.
– O momento linear e a posição de um elétron, ou outra partícula subatômica, não podem ser medidos ao mesmo tempo.
– A relação entre as duas variáveis é dada por uma desigualdade. De acordo com a Heisenberg, as variações de produto do momento e a posição da partícula é sempre maior do que a relação da constante de Planck (6.62606957 (29) x 10 -34 Jules x segundos) e 4n como detalhado na seguinte expressão matemática:

A legenda correspondente a esta expressão é a seguinte:
∆p: indeterminação do momento linear.
:X: indeterminação da posição.
h: Prancha constante.
π: número pi 3,14.
– Diante do exposto, o produto das incertezas tem a relação h / 4π como seu limite inferior, que é um valor constante. Portanto, se uma das magnitudes tende a zero, a outra deve aumentar na mesma proporção.
– Essa relação é válida para todos os pares de quantidades canônicas conjugadas. Por exemplo: o princípio da incerteza de Heisenberg é perfeitamente aplicável ao par energia-tempo, conforme detalhado abaixo:
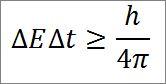
Nesta expressão:
∆E: indeterminação de energia.
:T: indeterminação do tempo.
h: Prancha constante.
π: número pi 3,14.
– Resulta deste modelo que o determinismo causal absoluto nas variáveis conjugadas canônicas é impossível, pois para estabelecer essa relação é preciso ter conhecimento sobre os valores iniciais das variáveis do estudo.
– Consequentemente, o modelo de Heisenberg é baseado em formulações probabilísticas, devido à aleatoriedade existente entre as variáveis nos níveis subatômicos.
Testes experimentais
O princípio da incerteza de Heisenberg surge como a única explicação possível para os testes experimentais que ocorreram durante as três primeiras décadas do século XXI.
Antes de Heisenberg enunciar o princípio da incerteza, os preceitos em vigor na época sugeriam que as variáveis momento linear, posição, momento angular, tempo, energia, entre outras, para partículas subatômicas fossem definidas operacionalmente.
Isso significava que eles eram tratados como se fossem física clássica; isto é, um valor inicial foi medido e o valor final foi estimado de acordo com o procedimento pré-estabelecido.
O exposto acima implica a definição de um sistema de referência para medições, o instrumento de medição e o método de uso do referido instrumento, de acordo com o método científico.
De acordo com isso, as variáveis descritas pelas partículas subatômicas devem se comportar deterministicamente. Ou seja, o comportamento deles teve que ser previsto com exatidão e precisão.
Entretanto, cada vez que um teste dessa natureza era realizado, era impossível obter o valor estimado teoricamente na medição.
As medições foram deturpadas devido às condições naturais do experimento, e o resultado obtido não foi útil para enriquecer a teoria atômica.
Exemplo
Por exemplo: se se trata de medir a velocidade e a posição de um elétron, a montagem do experimento deve contemplar a colisão de um fóton de luz com o elétron.
Essa colisão induz uma variação na velocidade e posição intrínseca do elétron, pelo que o objeto da medição é alterado por condições experimentais.
Portanto, o pesquisador incentiva a ocorrência de um erro experimental inevitável, apesar da exatidão e precisão dos instrumentos utilizados.
Mecânica quântica, exceto mecânica clássica
Além do acima, o princípio de indeterminação de Heisenberg afirma que, por definição, a mecânica quântica funciona de maneira diferente da mecânica clássica.
Consequentemente, supõe-se que o conhecimento preciso das medições do nível subatômico seja limitado pela linha fina que separa a mecânica clássica e a quântica.
Limitações
Apesar de explicar a indeterminação de partículas subatômicas e estabelecer as diferenças entre a mecânica clássica e a quântica, o modelo atômico de Heisenberg não estabelece uma única equação para explicar a aleatoriedade desse tipo de fenômeno.
Além disso, o fato de o relacionamento ser estabelecido por meio de uma desigualdade implica que o leque de possibilidades para o produto de duas variáveis conjugadas canônicas é indeterminado. Consequentemente, a incerteza inerente aos processos subatômicos é significativa.
Artigos de interesse
Modelo atômico de Schrödinger .
Modelo atômico de Broglie .
Modelo atômico de Chadwick .
Modelo atômico Perrin .
Modelo atômico de Thomson .
Modelo atômico de Dalton .
Modelo atômico de Dirac Jordan .
Modelo atômico de Demócrito .
Modelo atômico de Bohr .
Referências
- Beyler, R. (1998). Werner Heisenberg Encyclopædia Britannica, Inc. Recuperado de: britannica.com
- O Princípio da Incerteza de Heisenberg (sd). Recuperado de: hiru.eus
- García, J. (2012). Princípio da incerteza de Heisenberg. Recuperado de: hiberus.com
- Modelos atômicos (sf). Universidade Nacional Autônoma do México. Cidade do México, México. Recuperado de: asesorias.cuautitlan2.unam.mx
- Werner Heisenberg (sf). Obtido em: the-history-of-the-atom.wikispaces.com
- Wikipedia, A Enciclopédia Livre (2018). A prancha é constante. Recuperado de: en.wikipedia.org
- Wikipedia, A Enciclopédia Livre (2018). Relação de indeterminação de Heisenberg. Recuperado de: en.wikipedia.org