O modelo mecano-atlântico do átomo é uma representação simplificada da estrutura interna dos átomos, baseada na teoria desenvolvida por Niels Bohr em 1913. Neste modelo, os elétrons orbitam em torno do núcleo atômico em órbitas definidas, sem perder energia. O núcleo é composto por prótons e nêutrons, e os elétrons possuem cargas negativas. Este modelo ajuda a explicar o comportamento dos átomos em relação à sua reatividade química e suas propriedades físicas. Exemplos de elementos que se encaixam nesse modelo são o hidrogênio, hélio, oxigênio, entre outros. O modelo mecano-atlântico do átomo foi crucial para o desenvolvimento da química e da física modernas.
Comportamento dos elétrons no modelo quântico: descrição e análise detalhadas de suas propriedades.
No modelo quântico, os elétrons se comportam de maneira peculiar, seguindo as leis da mecânica quântica. Eles não possuem uma trajetória definida, mas sim uma distribuição de probabilidade de onde podem ser encontrados ao redor do núcleo do átomo. Isso é representado por orbitais eletrônicos, que são regiões do espaço onde a probabilidade de encontrar um elétron é maior.
Além disso, os elétrons possuem propriedades como spin, carga elétrica negativa e massa muito pequena. O seu comportamento é descrito por equações complexas, como a equação de Schrödinger, que descreve a evolução temporal da função de onda de um sistema quântico.
No modelo mecano-atlântico do átomo, os elétrons se distribuem ao redor do núcleo em diferentes níveis de energia, representados por camadas eletrônicas. Cada camada pode conter um número máximo de elétrons, de acordo com a regra do octeto.
Um exemplo de comportamento dos elétrons no modelo mecano-atlântico é a formação de ligações químicas. Quando os átomos compartilham elétrons, eles tendem a alcançar uma configuração eletrônica mais estável, preenchendo as camadas eletrônicas incompletas.
O estudo dessas propriedades é essencial para a compreensão da matéria e dos fenômenos químicos que ocorrem no nosso mundo.
Características fundamentais do modelo atômico proposto por Niels Bohr.
O modelo atômico proposto por Niels Bohr apresenta características fundamentais que revolucionaram a compreensão da estrutura dos átomos. Uma das principais inovações desse modelo é a ideia de que os elétrons se movem em órbitas circulares ao redor do núcleo, em níveis de energia bem definidos. Esses níveis de energia são quantizados, ou seja, possuem valores específicos e não podem assumir valores intermediários.
Além disso, o modelo de Bohr introduziu a noção de que os elétrons podem saltar de uma órbita para outra, absorvendo ou emitindo energia nesse processo. Quando um elétron salta de um nível de energia mais baixo para um mais alto, ele absorve energia. Por outro lado, quando ele volta para um nível de energia mais baixo, ele emite energia na forma de luz.
Essas características fundamentais do modelo atômico de Bohr explicam diversos fenômenos observados na natureza, como a emissão de luz por átomos excitados. Um exemplo clássico desse comportamento é o espectro de emissão do hidrogênio, que consiste em linhas espectrais bem definidas, cada uma correspondendo a um salto específico de um elétron entre níveis de energia.
Essas ideias fundamentais foram essenciais para o desenvolvimento da física quântica e continuam a ser relevantes para a compreensão do comportamento dos átomos e moléculas.
Conheça as principais características do modelo atômico vigente atualmente em estudo científico.
O modelo mecano-atlântico do átomo é o atualmente aceito pela comunidade científica. Esse modelo descreve o átomo como uma estrutura composta por um núcleo central, onde se encontram os prótons e nêutrons, e uma região externa onde os elétrons orbitam. Essa estrutura é semelhante a um sistema solar em miniatura, com o núcleo atuando como o sol e os elétrons como os planetas em órbita.
Uma das principais características desse modelo é a presença de camadas eletrônicas, onde os elétrons se distribuem de acordo com sua energia. Cada camada pode conter um número máximo de elétrons, seguindo a regra do octeto, que diz que os átomos tendem a ter 8 elétrons na camada de valência para ficarem estáveis.
Um exemplo de aplicação desse modelo é a explicação da formação de íons. Quando um átomo perde ou ganha elétrons, ele se torna um íon com carga positiva ou negativa, respectivamente. Isso ocorre devido à necessidade do átomo de atingir a estabilidade por meio da configuração eletrônica.
Sua aplicação vai desde a explicação de ligações químicas até a compreensão de reações químicas. É uma ferramenta essencial para a química moderna e para o avanço da ciência como um todo.
Qual é o modelo atômico atualmente aceito pela comunidade científica?
O modelo atômico atualmente aceito pela comunidade científica é o Modelo Mecano-Quântico do átomo. Este modelo foi desenvolvido a partir de diversas teorias e experimentos que permitiram a compreensão mais precisa da estrutura e comportamento dos átomos.
No Modelo Mecano-Quântico, os átomos são descritos como formados por um núcleo central composto por prótons e nêutrons, ao redor do qual orbitam os elétrons em diferentes níveis de energia. Estes elétrons não se movem de forma aleatória, mas sim em órbitas definidas e quantizadas.
Um dos princípios fundamentais deste modelo é o Princípio da Incerteza de Heisenberg, que estabelece que é impossível determinar com precisão a posição e a velocidade de uma partícula subatômica ao mesmo tempo. Além disso, a Teoria dos Orbitais Atômicos descreve a distribuição de probabilidade de encontrar os elétrons ao redor do núcleo.
O Modelo Mecano-Quântico do átomo é fundamental para a compreensão de diversos fenômenos químicos e físicos, como a formação de ligações químicas, a emissão de luz por átomos excitados e a estrutura da Tabela Periódica. É utilizado para explicar o comportamento dos átomos em diferentes situações e é amplamente aceito pela comunidade científica.
Sua aplicação é fundamental para o avanço da ciência e da tecnologia, permitindo a compreensão de diversos fenômenos observados no mundo microscópico.
Modelo mecano-atlântico do átomo: comportamento, exemplos
O modelo mecano-atlântico do átomo assume que ele é formado por um núcleo central composto de prótons e nêutrons. Os elétrons carregados negativamente envolvem o núcleo em regiões difusas conhecidas como orbitais .
A forma e extensão dos orbitais eletrônicos é determinada por várias magnitudes: o potencial do núcleo e os níveis quantificados de energia e momento angular dos elétrons.
De acordo com a mecânica quântica, os elétrons têm comportamento de dupla onda-partícula e, em escala atômica, são difusos e não pontuais.As dimensões do átomo são praticamente determinadas pela extensão dos orbitais eletrônicos que circundam o núcleo positivo.
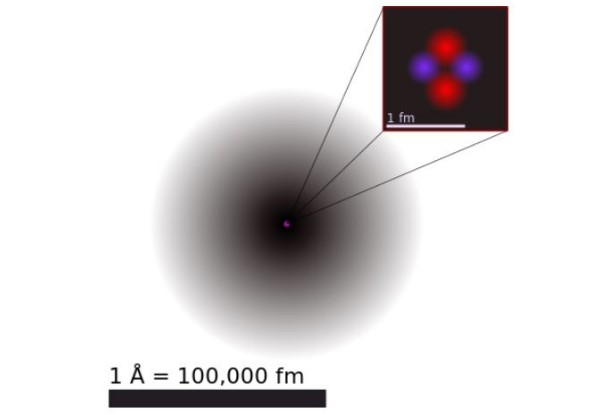
A Figura 1 mostra a estrutura do átomo de hélio, que possui um núcleo com dois prótons e dois nêutrons. Esse núcleo é cercado pela nuvem de probabilidade dos dois elétrons que circundam o núcleo, que é cem mil vezes menor. Na imagem a seguir, você pode ver o átomo de hélio, com prótons e nêutrons no núcleo e elétrons nos orbitais.
O tamanho de um átomo de hélio é da ordem de um angstrom (1 Å), ou seja, 1 x 10 ^ -10 m. Enquanto o tamanho de seu núcleo é da ordem de um femtômetro (1 fm), isso é 1 x 10 ^ -15 m.
Apesar de ser comparativamente pequeno, 99,9% do peso atômico está concentrado no pequeno núcleo. Isso ocorre porque os prótons e nêutrons são 2.000 vezes mais pesados que os elétrons que os cercam.
Escala atômica e comportamento quântico
Um dos conceitos que teve maior influência no desenvolvimento do modelo atômico foi o da dualidade onda-partícula: a descoberta de que cada objeto material tem uma onda de matéria associada a ele.
A fórmula que permite calcular o comprimento de onda λ associado a um objeto material foi proposta por Louis De Broglie em 1924 e é a seguinte:
λ = h / (mv)
Onde h é a constante de Planck, m a massa e v a velocidade.
De acordo com o princípio de De Broglie, todo objeto tem um comportamento duplo, mas, dependendo da escala das interações, da velocidade e da massa, o comportamento das ondas pode ser mais preeminente que o da partícula ou vice-versa.
O elétron é leve, sua massa é 9,1 × 10 ^ -31 kg. A velocidade típica de um elétron é de 6000 km / s (cinquenta vezes menor que a velocidade da luz). Essa velocidade corresponde aos valores de energia na faixa de dezenas de elétron-volts.
Com os dados acima, e usando a fórmula de De Broglie, o comprimento de onda do elétron pode ser obtido:
Qual é a raiz quadrada de 10 (-10) = (?) =? – Brainly.com.brMatemática
O elétron nas energias típicas dos níveis atômicos possui um comprimento de onda da mesma ordem de magnitude que o da escala atômica; portanto, nessa escala, ele tem um comportamento ondulatório e não- partícula.
Primeiros modelos quânticos
Com a ideia de que o elétron da escala atômica tem comportamento de onda, os primeiros modelos atômicos baseados em princípios quânticos foram desenvolvidos. Entre eles, destaca-se o modelo atômico de Bohr, que previa perfeitamente o espectro de emissão de hidrogênio, mas não o de outros átomos.
O modelo de Bohr e mais tarde o modelo de Sommerfeld eram modelos semi-clássicos. Ou seja, o elétron foi tratado como uma partícula sujeita à força de atração eletrostática do núcleo que orbitava ao redor dele, governado pela segunda lei de Newton.
Além das órbitas clássicas, esses primeiros modelos levaram em consideração que o elétron tinha uma onda de material associada. Somente as órbitas cujo perímetro era um número inteiro de comprimentos de onda foram permitidas, uma vez que aquelas que não atendem a esse critério desaparecem da interferência destrutiva.
É então que a quantização de energia na estrutura atômica aparece pela primeira vez.
A palavra quântica vem precisamente do fato de que o elétron só pode receber alguns valores discretos de energia dentro do átomo. Isso coincide com a descoberta de Planck, que consistiu na descoberta de que uma radiação de frequência f interage com a matéria nos pacotes de energia E = hf , onde h é a constante de Planck.
Dinâmica das ondas materiais
Não havia dúvida de que o elétron no nível atômico se comportava como uma onda material. O próximo passo foi encontrar a equação que governa seu comportamento. Essa equação não é nem mais nem menos que a equação de Schrodinger, proposta em 1925.
Esta equação refere-se e determina a função de onda ψ associado com uma partícula, tal como um electrão, com o seu potencial para a interacção e a sua energia total de E . Sua expressão matemática é:


A igualdade na equação de Schrodinger é alcançada apenas para alguns valores da energia total E , resultando na quantização da energia.A função de onda dos elétrons sujeitos ao potencial do núcleo é obtida a partir da solução da equação de Schrodinger.
Orbitais atômicos
O valor absoluto da função de onda ao quadrado | , | ^ 2, fornece a amplitude de probabilidade de encontrar o elétron em uma determinada posição.
Isso leva ao conceito de orbital, que é definido como a região difusa que o elétron ocupa com amplitude de probabilidade diferente de zero, para valores discretos de energia e momento angular determinados pelas soluções da equação de Schrodinger.
O conhecimento dos orbitais é muito importante, pois descreve a estrutura atômica, a reatividade química e as possíveis ligações para formar moléculas.
O átomo de hidrogênio é o mais simples de todos, possuindo um elétron solitário e é o único que admite uma solução analítica exata da equação de Schrodinger.
Esse átomo simples possui um núcleo formado por um próton, que produz um potencial central de atração coulombiana que depende apenas do raio r , sendo um sistema com simetria esférica.
A função de onda depende da posição, dada pelas coordenadas esféricas em relação ao núcleo, uma vez que o potencial elétrico possui simetria central.
Além disso, a função de onda pode ser escrita como o produto de uma função que depende exclusivamente da coordenada radial e outra que depende das coordenadas angulares:

Números quânticos
A solução da equação radial produz os valores discretos de energia, que dependem de um número inteiro n, chamado número quântico principal , que pode assumir valores inteiros positivos 1, 2, 3, …
Valores de energia discreta são valores negativos dados pela seguinte fórmula:

A equação angular solução define os valores quantificados de momento angular e o componente de z, resultando números quânticos l e ml .
O número quântico de momento angular l varia de 0 a n-1 . O número quântico ml é chamado número quântico magnético e varia de -l a + l . Por exemplo, se eu fosse 2, o número quântico magnético assumiria os valores -2, -1, 0, 1, 2.
Forma e tamanho dos orbitais
O alcance radial do orbital é determinado pela função de onda de rádio em. É maior à medida que a energia do elétron cresce, ou seja, à medida que o número quântico principal aumenta.
A distância radial é geralmente medida em raios de Bohr, que para a menor energia de hidrogênio é de 5,3 X 10 -11 m = 0,53 Å.

Mas a forma dos orbitais é determinada pelo valor do número quântico de momento angular. Se l = 0 você tem um orbital esférico chamado s, se l = 1 você tem um orbital lobulado chamado p , que pode ter três orientações de acordo com o número quântico magnético. A figura a seguir mostra a forma dos orbitais.
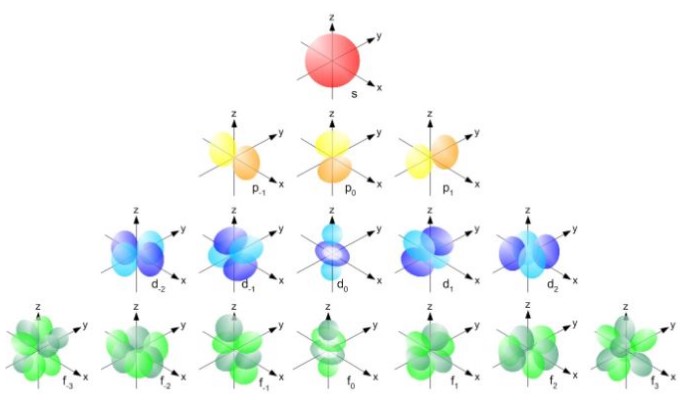
Esses orbitais são empacotados um dentro do outro de acordo com a energia dos elétrons. Por exemplo, a figura a seguir mostra os orbitais em um átomo de sódio.

Spin
O modelo mecânico quântico da equação de Schrödinger não incorpora o spin do elétron. Mas isso é levado em consideração pelo princípio de exclusão de Pauli, que indica que os orbitais podem ser preenchidos com até dois elétrons com números de spin quântico s = + ½ es = -½.
Por exemplo, o íon sódio tem 10 elétrons, ou seja, se nos referirmos à figura anterior, existem dois elétrons para cada orbital.
Mas se é o átomo neutro de sódio, existem 11 elétrons, o último dos quais ocuparia um orbital 3s (não mostrado na figura e com raio maior que os 2s). A rotação do átomo é determinante nas características magnéticas de uma substância.
Referências
- Alonso – Finn. Fundamentos quânticos e estatísticos. Addison Wesley
- Eisberg – Resnick. Física quântica. Limusa – Wiley.
- Gasiorowicz Física quântica John Wiley & Sons.
- HSC Curso de Física 2. Jacaranda plus.
- Wikipedia Modelo atômico de Schrodinger. Recuperado de: Wikipedia.com