Os números compostos são aqueles que possuem mais de dois divisores, ou seja, além de serem divisíveis por 1 e por si mesmos, também podem ser divididos por outros números.
Neste artigo, abordaremos as características dos números compostos, como identificá-los, exemplos de números compostos e como realizar a decomposição em fatores primos. Além disso, apresentaremos diversos exercícios para praticar e aprofundar o conhecimento sobre esse tema.
Os números compostos desempenham um papel importante na matemática, sendo essencial compreender suas propriedades e aplicações. Vamos explorar mais sobre esse assunto e aprimorar nossas habilidades matemáticas.
Exemplos de números compostos que você precisa conhecer.
Números compostos são aqueles que possuem mais de dois divisores, ou seja, além de 1 e do próprio número. É importante conhecer alguns exemplos de números compostos para entender melhor esse conceito matemático.
Um exemplo de número composto é o 6, que possui os divisores 1, 2, 3 e 6. Outro exemplo é o 15, que possui os divisores 1, 3, 5 e 15. Já o número 21 é outro exemplo de número composto, pois possui os divisores 1, 3, 7 e 21.
É importante destacar que os números primos são aqueles que possuem apenas dois divisores: 1 e o próprio número. Portanto, os números compostos são todos os números que não são primos.
Para identificar se um número é composto, basta verificar se ele possui mais de dois divisores. Caso contrário, ele será considerado um número primo.
Agora que você conhece alguns exemplos de números compostos, pratique identificando outros números compostos e primos. Isso ajudará a reforçar o seu conhecimento sobre esses conceitos matemáticos.
Entendendo os números compostos na matemática do 5º ano escolar.
Números compostos são aqueles que têm mais de dois divisores, ou seja, além de serem divisíveis por 1 e por eles mesmos, também são divisíveis por outros números. Para entender melhor, é importante saber que os números primos são aqueles que têm apenas dois divisores: 1 e o próprio número. Já os números compostos têm mais de dois divisores, o que os torna diferentes dos números primos.
Um exemplo de número composto é o 6, pois ele é divisível por 1, 2, 3 e 6. Já o número 7, por exemplo, é um número primo, pois é divisível apenas por 1 e por 7. Outro exemplo de número composto é o 10, que é divisível por 1, 2, 5 e 10.
Para identificar se um número é composto, basta verificar se ele tem mais de dois divisores. Caso tenha apenas dois divisores, ele será um número primo. Os números compostos são muito úteis em matemática, pois ajudam a compreender melhor a divisibilidade e a fatoração de números.
Agora, vamos resolver alguns exercícios para praticar o conceito de números compostos:
Exercício 1: Identifique se os números a seguir são primos ou compostos: 12, 17, 21, 29.
Exercício 2: Escreva os divisores de cada número composto a seguir: 8, 15, 20, 25.
Espero que com esses exemplos e exercícios você tenha compreendido melhor o conceito de números compostos e consiga aplicá-los em seus estudos de matemática do 5º ano escolar.
Como reconhecer um número composto através de suas divisões por diferentes valores.
Para reconhecer um número composto através de suas divisões por diferentes valores, é importante entender o conceito de números compostos. Os números compostos são aqueles que possuem mais de dois divisores, ou seja, além de serem divisíveis por 1 e por ele mesmo, também podem ser divididos por outros números.
Uma forma de identificar um número composto é realizar divisões por diferentes valores. Ao fazer isso, se o número em questão for divisível por um número diferente de 1 e de si mesmo, então ele é um número composto. Por exemplo, se estivermos analisando o número 12, podemos dividí-lo por 2, 3, 4, 6 e 12. Como 12 é divisível por 2, 3 e 4, ele é considerado um número composto.
Outra maneira de reconhecer um número composto é observar se ele possui mais de dois divisores. Por exemplo, o número 15 possui os divisores 1, 3, 5 e 15, o que significa que ele é um número composto.
É importante ressaltar que nem todo número que possui mais de dois divisores é composto. Por exemplo, o número 1 possui infinitos divisores, mas é considerado um número primo por ser divisível apenas por 1 e por ele mesmo.
Portanto, ao analisar um número e realizar suas divisões por diferentes valores, é possível identificar se ele é um número composto ou não, levando em consideração a quantidade de divisores que possui.
Entenda o conceito de números compostos de forma simples e clara.
Números compostos: são aqueles que possuem mais de dois divisores, ou seja, além de serem divisíveis por 1 e por eles mesmos, também podem ser divididos por outros números. Em contrapartida, os números primos são aqueles que têm apenas dois divisores: 1 e o próprio número.
Para identificar se um número é composto, basta verificar se ele possui mais de dois divisores. Por exemplo, o número 6 é composto, pois pode ser dividido por 1, 2, 3 e 6. Já o número 7 é primo, pois só pode ser dividido por 1 e 7.
Os números compostos são essenciais na matemática, pois podem ser decompostos em fatores primos, facilitando a resolução de problemas de divisão e multiplicação. Por exemplo, o número 24 pode ser decomposto em fatores primos como 2 x 2 x 2 x 3.
Para praticar o reconhecimento de números compostos, é possível realizar alguns exercícios. Por exemplo, identifique se os números a seguir são compostos ou primos: 10, 13, 18, 23, 28. Lembre-se de que os números primos têm apenas dois divisores!
Números compostos: características, exemplos, exercícios
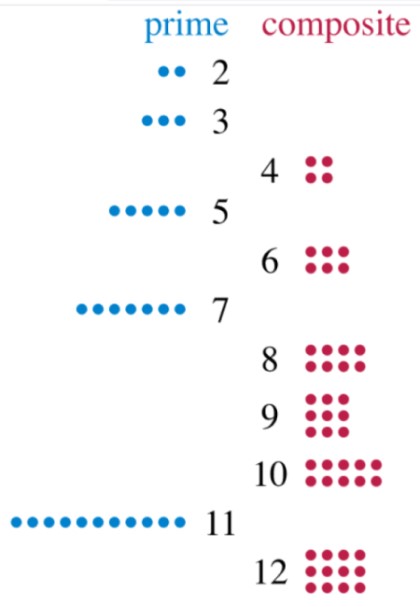
Os números dos compostos são aqueles números inteiros que possuem mais de dois divisores. Se olharmos atentamente, todos os números são pelo menos exatamente divisíveis entre si e entre 1. Aqueles que possuem apenas esses dois divisores são chamados primos e aqueles que têm mais são compostos.
Vejamos o número 2, que só pode ser dividido entre 1 e 2. O número 3 também possui dois divisores: 1 e 3. Portanto, ambos são primos. Agora, vejamos o número 12, que podemos dividir exatamente por 2, 3, 4, 6 e 12. Tendo 5 divisores, 12 é um número composto.
E o que acontece com o número 1, aquele que divide todos os outros? Bem, não é primo, porque não possui dois divisores e não é composto, portanto, 1 não se enquadra em nenhuma dessas duas categorias. Mas existem muitos mais números que o fazem.
Os números compostos podem ser expressos como o produto de números primos, e esse produto, exceto pela ordem dos fatores, é exclusivo para cada número. Isso é assegurado pelo teorema fundamental da aritmética provado pelo matemático grego Euclides (325-365 aC).
Voltemos ao número 12, que podemos expressar de várias maneiras. Vamos tentar alguns:
12 = 4 x 3 = 2 x 6 = 12 x 1 = 2 2 x 3 = 3 x 2 2 = 3 x 2 x 2 = 2 x 2 x 3 = 2 x 3 x 2
As formas destacadas em negrito são produtos de números primos e a única coisa que muda é a ordem dos fatores, que sabemos que não altera o produto. As outras formas, embora válidas para expressar 12, não consistem apenas em números primos.
Exemplos de números compostos
Se quisermos decompor um número composto em seus fatores primos, devemos dividi-lo por números primos de modo que a divisão seja exata, ou seja, que o restante seja 0.
Esse procedimento é chamado de decomposição de fator primário ou decomposição canônica. Os fatores primos podem ser elevados para expoentes positivos.
Vamos decompor o número 570, observando que ele é par e, portanto, divisível por 2, que é um número primo.
Usaremos uma barra para separar o número à esquerda dos divisores à direita. Os respectivos quocientes são colocados abaixo do número à medida que são obtidos. A decomposição está completa quando o último número na coluna da esquerda é 1:
570 │2
285 │
Ao dividir por 2, o quociente é 285, que é divisível por 5, outro número primo, para terminar em 5.
570 │2
285 │5
57 │
O 57 é divisível por 3, também um primo, pois a soma dos seus dígitos 5 +7 = 12 é um múltiplo de 3.
570 │2
285 │5
57 │3
19 │
Finalmente, obtemos 19, que é um número primo, cujos divisores são 19 e 1:
570 │2
285 │5
57 │3
19 │19
1 │
Ao obter 1, já podemos expressar 570 assim:
570 = 2 x 5 x 3 x 19
E vemos que é realmente o produto de 4 números primos.
Neste exemplo, começamos dividindo por 2, mas os mesmos fatores (em outra ordem) seriam obtidos se começássemos dividindo por 5, por exemplo.
Critérios de divisibilidade
Para decompor um número composto em seus fatores primos, é necessário dividi-lo exatamente. Os critérios de divisibilidade entre números primos são regras que permitem saber quando um número é exatamente divisível por outro, sem ter que testar ou tentar.
– Divisibilidade entre 2
Todo número par, aqueles que terminam em 0 ou um número par são divisíveis por 2.
– Divisibilidade entre 3
Se a soma dos dígitos de um número for um múltiplo de 3, o número também será, portanto, divisível por 3.
– Divisibilidade entre 5
Os números que terminam em 0 ou 5 são divisíveis por 5.
-Divisibilidade entre 7
Um número é divisível por 7 se, separando o último número, multiplicando-o por 2 e subtraindo o número restante, o valor resultante é um múltiplo de 7.
Essa regra parece um pouco mais complicada do que as anteriores, mas na realidade não é muito, então vamos ver um exemplo: será 98 divisível por 7?
Vamos seguir as instruções: separamos o último número que é 8, multiplicamos por 2 que dá 16. O número que resta ao separar o 8 é 9. Subtraia 16 – 9 = 7. E como 7 é um múltiplo, 98 é divisível entre 7.
-Divisibilidade entre 11
Se a soma dos números na posição par (2, 4, 6 …) for subtraída da soma dos números na posição ímpar (1, 3, 5, 7 …) e for obtido 0 ou um múltiplo de 11, o número será divisível por 11.
Os primeiros múltiplos de 11 são facilmente identificados: são 11, 22, 33, 44 … 99. Mas tenha cuidado, 111 não é, mas 110 é.
Como exemplo, vamos ver se 143 é um múltiplo de 11.
Esse número tem 3 dígitos, o único número par é 4 (o segundo), os dois números ímpares são 1 e 3 (primeiro e terceiro) e sua soma é 4.
Ambas as somas são subtraídas: 4 – 4 = 0 e, como 0 é obtido, verifica-se que 143 é um múltiplo de 11.
-Divisibilidade entre 13
O número sem o dígito das unidades deve ser subtraído 9 vezes esse dígito. Se a conta fornecer 0 ou múltiplo de 13, o número será múltiplo de 13.
Como exemplo, verificaremos se 156 é um múltiplo de 13. O dígito das unidades é 6 e o número que permanece sem ele é 15. Multiplicamos 6 x 9 = 54 e agora subtraímos 54 – 15 = 39.
Mas 39 é 3 x 13, então 56 é um múltiplo de 13.
Números primos entre si
Dois ou mais números primos ou compostos podem ser primos um para o outro ou coprime. Isso significa que o único divisor comum que eles têm é 1.
Há duas propriedades importantes a serem lembradas sobre coprimes:
-Dois, três e mais números consecutivos são sempre primos um para o outro.
-O mesmo pode ser dito de dois, três ou mais números ímpares consecutivos.
Por exemplo, 15, 16 e 17 são números primos entre si e 15, 17 e 19.
Como descobrir quantos divisores um número composto possui
Um número primo tem dois divisores, o mesmo número e 1. E quantos divisores um número composto possui? Estes podem ser primos ou compostos.
Seja N um número composto expresso em termos de sua decomposição canônica da seguinte maneira:
N = a n . b m . c p … r k
Onde a, b, c … r são os fatores primos en, m, p … k são os respectivos expoentes. Bem, o número de divisores C que N possui é dado por:
C = (n +1) (m + 1) (p + 1) … (k + 1)
Com C = divisores primos + divisores compostos + 1
Por exemplo 570, que é expresso assim:
570 = 2 x 5 x 3 x 19
Todos os fatores primos são aumentados para 1, portanto, 570 tem:
C = (1 + 1) (1 + 1) (1+ 1) (1 +1) = 16 divisores
Desses 10 divisores, já sabemos: 1, 2, 3, 5, 19 e 570. Faltam mais 10 divisores, que são números compostos: 6, 10, 15, 30, 38, 57, 95, 114, 190 e 285. Eles estão observando a decomposição em fatores primos e também multiplicando combinações desses fatores entre si.
Exercícios resolvidos
– Exercício 1
Decomponha os seguintes números em fatores primos:
a) 98
b) 143
c) 540
d) 3705
Solução para
98 │2
49 │7
7 │7
1 │
98 = 2 x 7 x 7
Solução b
143 1311
13 │13
1 │
143 = 11 x 13
Solução c
540 1085
108 │2
54 │2
27 │3
9 │3
3 │3
1 │
540 = 5 x 2 x 2 x 3 x 3 x 3 = 5 x 2 2 x 3 3
Solução d
3705 75
741 │3
247 │13
19 │19
1 │
3705 = 5 x 3 x 13 x 19
– Exercício 2
Descubra se os seguintes números são primos um ao outro:
6, 14, 9
Solução
-Os divisores de 6 são: 1, 2, 3, 6
-Como para 14, é divisível por: 1, 2, 7, 14
-Finalmente 9 tem como divisores: 1, 3, 9
O único divisor que eles têm em comum é 1, então eles são primos um para o outro.
Referências
- Baldor, A. 1986. Aritmética. Códice de Edições e Distribuições.
- Byju’s. Números primos e compostos. Recuperado de: byjus.com.
- Números primos e compostos. Recuperado de: profeyennyvivaslapresentacion.files.wordpress.com
- Smartick. Critérios de divisibilidade. Recuperado de: smartick.es.
- Wikipedia. Números compostos. Recuperado de: en.wikipedia.org.