As ondas mecânicas são perturbações que se propagam em um meio material, como o ar, a água ou sólidos, devido à sua elasticidade. Elas possuem características e propriedades específicas, como amplitude, frequência, comprimento de onda e velocidade de propagação. As fórmulas matemáticas utilizadas para descrever as ondas mecânicas incluem a equação da velocidade de propagação e a equação da frequência. Existem diversos tipos de ondas mecânicas, como as ondas longitudinais, transversais e de superfície, cada uma com suas particularidades e aplicações específicas em diversas áreas da física e engenharia.
Tipos de ondas: descubra os 4 principais tipos de ondas existentes na natureza.
As ondas são um fenômeno comum na natureza, e existem diversos tipos que podem ser classificados de acordo com suas características e propriedades. No entanto, existem quatro principais tipos de ondas que são amplamente estudados e observados: ondas mecânicas, ondas sonoras, ondas eletromagnéticas e ondas gravitacionais.
As ondas mecânicas são aquelas que necessitam de um meio material para se propagar, como a água, o ar ou um sólido. Elas podem ser classificadas em duas categorias principais: ondas transversais e ondas longitudinais. Nas ondas transversais, a vibração é perpendicular à direção de propagação da onda, enquanto nas ondas longitudinais, a vibração é paralela à direção de propagação.
As ondas sonoras são um tipo específico de onda mecânica, onde a propagação da vibração ocorre através de um meio material, como o ar. Elas são responsáveis pela percepção auditiva dos seres vivos e possuem características como frequência, amplitude e velocidade de propagação.
As ondas eletromagnéticas são ondas que não necessitam de um meio material para se propagar, e são compostas por campos elétricos e magnéticos que oscilam perpendicularmente entre si. Elas incluem desde as ondas de rádio até os raios gama, e se propagam à velocidade da luz no vácuo.
Por fim, as ondas gravitacionais são ondulações no espaço-tempo causadas por eventos cósmicos violentos, como a colisão de buracos negros. Elas foram previstas por Albert Einstein em sua teoria da relatividade geral e, em 2015, foram detectadas pela primeira vez por observatórios astronômicos.
Em resumo, os quatro principais tipos de ondas na natureza são as ondas mecânicas, ondas sonoras, ondas eletromagnéticas e ondas gravitacionais, cada uma com características e propriedades únicas que as tornam fundamentais para a compreensão do universo e dos fenômenos físicos que nos cercam.
Fórmulas para calcular diferentes tipos de ondas e suas propriedades físicas.
As ondas mecânicas são perturbações que se propagam em um meio material, como ondas sonoras, ondas em cordas e ondas em molas. Para calcular diferentes tipos de ondas e suas propriedades físicas, é importante conhecer algumas fórmulas fundamentais.
Velocidade da onda:
A velocidade de propagação de uma onda em um meio material pode ser calculada pela fórmula v = λ*f, onde v é a velocidade da onda, λ é o comprimento de onda e f é a frequência da onda.
Frequência da onda:
A frequência de uma onda é o número de ciclos que a onda completa em um segundo e pode ser calculada pela fórmula f = v/λ, onde f é a frequência da onda, v é a velocidade da onda e λ é o comprimento de onda.
Amplitude da onda:
A amplitude de uma onda é a distância vertical máxima entre o ponto de equilíbrio e a crista da onda. A amplitude pode ser calculada diretamente a partir da equação que descreve o tipo específico de onda.
Período da onda:
O período de uma onda é o tempo que a onda leva para completar um ciclo. O período pode ser calculado pela fórmula T = 1/f, onde T é o período da onda e f é a frequência da onda.
Intensidade da onda:
A intensidade de uma onda é a quantidade de energia que a onda transporta por unidade de área perpendicular à direção de propagação da onda. A intensidade pode ser calculada pela fórmula I = P/A, onde I é a intensidade da onda, P é a potência total transportada pela onda e A é a área perpendicular à direção de propagação da onda.
Com o conhecimento dessas fórmulas, é possível calcular diferentes propriedades físicas das ondas mecânicas e compreender melhor seu comportamento e características.
Características das ondas: quais são suas propriedades e como se comportam?
As ondas mecânicas são perturbações que se propagam em um meio material, levando energia de um lugar para outro sem que haja transporte de matéria. Elas possuem diversas características que as distinguem, como amplitude, comprimento de onda, frequência e velocidade de propagação.
Uma das propriedades mais importantes das ondas é a amplitude, que representa a máxima distância de deslocamento das partículas do meio em relação à posição de equilíbrio. Quanto maior a amplitude, maior a energia transportada pela onda. Já o comprimento de onda é a distância entre dois pontos consecutivos que estão em fase, ou seja, que se encontram na mesma posição de oscilação.
A frequência das ondas é o número de oscilações que ocorrem em um determinado intervalo de tempo. Ela é medida em hertz (Hz) e está relacionada com a quantidade de ondas que passam por um ponto em um segundo. Por fim, a velocidade de propagação das ondas é a distância percorrida pela onda em um determinado intervalo de tempo. Ela é calculada pela fórmula: v = λ * f, onde v é a velocidade, λ é o comprimento de onda e f é a frequência.
Existem diversos tipos de ondas mecânicas, sendo as mais comuns as ondas longitudinais e as ondas transversais. As ondas longitudinais se propagam na mesma direção de vibração das partículas do meio, como as ondas sonoras. Já as ondas transversais se propagam perpendicularmente à direção de vibração das partículas, como as ondas em uma corda.
Em resumo, as ondas mecânicas possuem características únicas que as tornam essenciais para a transmissão de energia e informação. Compreender suas propriedades e fórmulas é fundamental para o estudo e aplicação de diversos fenômenos físicos e naturais.
Descubra os 7 tipos de ondas presentes na natureza e suas características únicas.
As ondas são um fenômeno natural que pode ser observado em diversos contextos, desde o movimento do mar até o som que ouvimos. Existem sete tipos principais de ondas presentes na natureza, cada um com características únicas que os distinguem.
As ondas mecânicas são um dos tipos mais comuns de ondas e são caracterizadas pela necessidade de um meio material para se propagarem. Isso significa que as ondas mecânicas não podem se mover no vácuo, por exemplo. Elas podem ser classificadas em diferentes tipos, dependendo de suas propriedades e características.
Algumas das propriedades das ondas mecânicas incluem a amplitude, que é a altura máxima da onda em relação à sua posição de equilíbrio, e o comprimento de onda, que é a distância entre dois pontos consecutivos da onda que estão em fase. Além disso, a frequência das ondas mecânicas está relacionada à quantidade de ciclos que a onda completa em um determinado período de tempo.
Existem diversos tipos de ondas mecânicas, cada um com características únicas. Alguns exemplos incluem as ondas sonoras, que são ondas mecânicas que se propagam através de meios materiais, como o ar ou a água. Outro exemplo são as ondas sísmicas, que são geradas por terremotos e se propagam através da crosta terrestre.
Para descrever as ondas mecânicas, podemos utilizar diversas fórmulas matemáticas, como a velocidade de propagação da onda, que é determinada pela frequência e comprimento de onda da onda. Além disso, a energia transportada por uma onda mecânica está relacionada à sua amplitude e frequência.
Em resumo, as ondas mecânicas são um fenômeno natural fascinante, com diversas propriedades e características únicas. Ao compreender melhor os diferentes tipos de ondas mecânicas e suas fórmulas associadas, podemos aprimorar nosso conhecimento sobre esse importante aspecto da natureza.
Ondas mecânicas: características, propriedades, fórmulas, tipos
Uma onda mecânica é uma perturbação que precisa de um meio físico para se espalhar. O exemplo mais próximo é o som, capaz de ser transmitido através de um gás, um líquido ou um sólido.
Outras ondas mecânicas conhecidas são aquelas que ocorrem quando a corda tensa de um instrumento musical é pressionada. Ou as ondulações tipicamente circulares causadas por uma pedra jogada em um lago.

A perturbação viaja através do meio produzindo vários deslocamentos nas partículas que o compõem, dependendo do tipo de onda. À medida que a onda passa, cada partícula no meio executa movimentos repetitivos que a separam brevemente de sua posição de equilíbrio.
A duração do distúrbio depende de sua energia. No movimento das ondas, energia é o que se propaga de um lado para o outro do ambiente, uma vez que as partículas vibrantes nunca se movem muito longe de seu local de origem.
A onda e a energia que ela carrega podem percorrer grandes distâncias. Quando a onda desaparece, é porque sua energia acabou se dissipando no meio, deixando tudo tão calmo e quieto quanto antes da perturbação.
Tipos de ondas mecânicas
As ondas mecânicas são classificadas em três grupos principais:
– ondas transversais.
– ondas longitudinais.
– ondas de superfície.
Ondas transversais
Nas ondas transversais, as partículas se movem perpendicularmente à direção da propagação. Por exemplo, as partículas na sequência na figura a seguir oscilam verticalmente enquanto a onda se move da esquerda para a direita:

Ondas longitudinais
Nas ondas longitudinais, a direção de propagação e a direção do movimento das partículas são paralelas.

Ondas de superfície
Uma onda do mar combina ondas longitudinais e ondas transversais na superfície, portanto são ondas superficiais, viajando pela fronteira entre dois meios diferentes: água e ar, como mostra a figura a seguir.
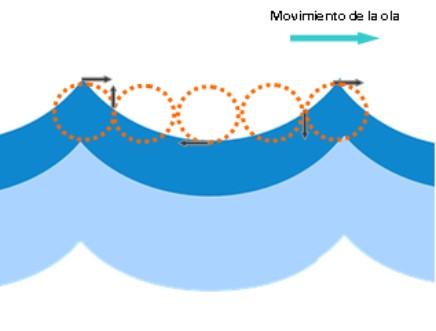
Ao quebrar as ondas na costa, os componentes longitudinais predominam. Portanto, observa-se que as algas próximas à costa têm um movimento alternativo.
Exemplos dos diferentes tipos de ondas: movimentos sísmicos
Durante os terremotos, existem vários tipos de ondas que se movem pelo globo, incluindo ondas longitudinais e transversais.
As ondas sísmicas longitudinais são chamadas de ondas P, enquanto as ondas transversais são ondas S.
A denominação P se deve ao fato de serem ondas de pressão e também serem primárias quando chegam primeiro, enquanto as transversais são S por “cisalhamento” ou cisalhamento e também são secundárias, pois chegam após o P.
Características e propriedades
As ondas amarelas na Figura 2 são ondas periódicas, que consistem em distúrbios idênticos que se movem da esquerda para a direita. Note-se que tanto um e b tem o mesmo valor em cada uma das regiões da onda.
As perturbações da onda periódica são repetidas no tempo e no espaço, adotando a forma de curva sinusoidal caracterizada por ter cristas ou picos, que são os pontos mais altos, e vales, onde os pontos mais baixos estão.
Este exemplo será usado para estudar as características mais importantes das ondas mecânicas.
Comprimento de onda e comprimento de onda
Supondo que a onda na Figura 2 represente uma corda vibratória, a linha preta serve como referência e divide o trem de ondas em duas partes simétricas. Essa linha coincidirá com a posição em que a corda está em repouso.
O valor de a é chamado de amplitude da onda e é geralmente indicado pela letra A. Por seu lado, a distância entre dois vales ou duas cristas sucessivas é o comprimento de onda l e corresponde à magnitude chamada b na Figura 2.
Período e frequência
Sendo um fenômeno repetitivo no tempo, a onda possui um período T, que é o tempo necessário para executar um ciclo completo, enquanto a frequência f é inversa ou recíproca do período e corresponde ao número de ciclos realizados por unidade de tempo .
A frequência f tem como unidades no Sistema Internacional o inverso do tempo: s -1 ou Hertz, em homenagem a Heinrich Hertz, que descobriu as ondas de rádio em 1886. 1 Hz é interpretado como a frequência equivalente a um ciclo ou vibração por segundo.
A velocidade v da onda relaciona a frequência ao comprimento de onda:
v = λ.f = l / T
Freqüência angular
Outro conceito útil é a frequência angular ω dada por:
ω = 2πf
A velocidade das ondas mecânicas é diferente dependendo do meio em que elas viajam. Como regra geral, as ondas mecânicas têm maior velocidade quando viajam por um sólido e são mais lentas em gases, incluindo a atmosfera.
Em geral, a velocidade de muitos tipos de ondas mecânicas é calculada pela seguinte expressão:

Por exemplo, para uma onda que se propaga ao longo de uma sequência, a velocidade é dada por:
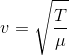
A tensão na corda tende a devolvê-la à sua posição de equilíbrio, enquanto a densidade de massa impede que isso aconteça imediatamente.
Fórmulas e equações
As seguintes equações são úteis para resolver os seguintes exercícios:
Frequência angular:
ω = 2πf
Período:
T = 1 / f
Densidade de massa linear:

v = λ.f
v = λ / T
v = λ / 2π
Velocidade da onda que se propaga em uma string:
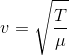
Exemplos resolvidos
Exercício 1
A onda senoidal mostrada na Figura 2 se move na direção do eixo x positivo e tem uma frequência de 18,0 Hz. Sabe-se que 2a = 8,26 cm eb / 2 = 5,20 cm. Localizar:
a) Amplitude.
b) Comprimento de onda.
c) Período.
d) velocidade da onda.
Solução
a) A amplitude é a = 8,26 cm / 2 = 4,13 cm
b) O comprimento de onda é l = b = 2 x20 cm = 10,4 cm.
c) O período T é o inverso da frequência, portanto T = 1 / 18,0 Hz = 0,056 s.
d) A velocidade da onda é v = lf = 10,4 cm. 18 Hz = 187,2 cm / s.
Exercício 2
Um fio fino de 75 cm de comprimento tem uma massa de 16,5 g. Uma das extremidades é fixada na haste, enquanto a outra possui um parafuso que permite ajustar a tensão no fio. Calcular:
a) A velocidade desta onda.
b) A tensão em Newton necessária para que uma onda transversal com comprimento de onda de 3,33 cm vibre a uma taxa de 625 ciclos por segundo.
Solução
a) Usando v = λ.f, válido para qualquer onda mecânica e substituindo valores numéricos, você obtém:
v = 3,33 cm x 625 ciclos / segundo = 2081,3 cm / s = 20,8 m / s
b) A velocidade da onda que se propaga através de uma corda é:
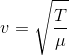

A tensão T na corda é obtida elevando-a ao quadrado de ambos os lados da igualdade e limpando:
T = v 2 .μ = 20,8 2 . 2,2 x 10 -6 N = 9,52 x 10 -4 N.
O som: uma onda longitudinal
O som é uma onda longitudinal, muito fácil de visualizar. Para isso, é necessária apenas uma furtiva , uma mola helicoidal flexível com a qual muitas experiências podem ser realizadas para determinar a forma das ondas.
Uma onda longitudinal consiste em um pulso que comprime e expande o meio por sua vez. A área comprimida é chamada de “compressão” e a área onde as espirais da mola estão mais separadas é a “expansão” ou “rarefação”. Ambas as zonas se movem ao longo do eixo axial do slinky e formam uma onda longitudinal.

Da mesma maneira que uma parte da doca é comprimida e a outra se estende à medida que a energia se move ao longo da onda, o som comprime partes do ar ao redor da fonte que emite a perturbação. Por esse motivo, não pode se espalhar no vácuo.
Para as ondas longitudinais, os parâmetros descritos acima para ondas transversais periódicas são igualmente válidos: amplitude, comprimento de onda, período, frequência e velocidade da onda.
A Figura 5 mostra o comprimento de onda de uma onda longitudinal que viaja ao longo de uma mola helicoidal.
Nele, dois pontos localizados no centro de duas compressões sucessivas foram selecionados para indicar o valor do comprimento de onda.
As compressões são equivalentes às cristas e as expansões são dos vales em uma onda transversal; portanto, uma onda sonora também pode ser representada por uma onda senoidal.
Características do som: frequência e intensidade
O som é um tipo de onda mecânica com várias propriedades muito especiais, que a distinguem dos exemplos que vimos até agora. A seguir, veremos quais são suas propriedades mais relevantes.
Frequência
A frequência do som é percebida pelo ouvido humano como som agudo (altas frequências) ou grave (baixas frequências).
A faixa de frequência audível no ouvido humano está entre 20 e 20.000 Hz. Acima de 20.000 Hz são os chamados sons de ultrassom e abaixo do infra-som, frequências inaudíveis aos seres humanos, mas que cães e outros animais podem perceber e use
Por exemplo, os morcegos emitem ondas de ultrassom com o nariz para determinar sua localização no escuro e também por meio de comunicação.
Esses animais possuem sensores com os quais recebem as ondas refletidas e, de alguma forma, interpretam o tempo de atraso entre a onda emitida e a refletida e as diferenças em sua frequência e intensidade. Com esses dados, eles inferem a distância que percorreram e, dessa maneira, são capazes de saber onde estão os insetos e voar entre as fendas das cavernas que habitam.
Mamíferos marinhos como a baleia e o golfinho têm um sistema semelhante: possuem órgãos especializados cheios de gordura em suas cabeças, com os quais emitem sons, e os sensores correspondentes em suas mandíbulas, que detectam o som refletido. Este sistema é conhecido como ecolocalização.
Intensidade
A intensidade da onda sonora é definida como a energia transportada por unidade de tempo e por unidade de área. Energia por unidade de tempo é energia . Portanto, a intensidade do som é a energia por unidade de área e vem em watts / m 2 ou W / m 2 . O ouvido humano percebe a intensidade da onda como volume: quanto mais volume a música tiver, mais intensa será.
O ouvido detecta intensidades entre 10-12 e 1 W / m 2 sem sentir dor, mas a relação entre intensidade e volume percebido não é linear. Para produzir um som com o dobro do volume, é necessária uma onda com 10 vezes mais intensidade.
O nível de intensidade sonora é uma intensidade relativa medida em uma escala logarítmica, na qual a unidade é o bel e, na maioria das vezes, o decibel ou decibel.
O nível de intensidade sonora é indicado como β e é dado em decibéis por:
β = 10 log (I / I ou )
Onde I é a intensidade do som e I ou é um nível de referência que é considerado o limiar da audição em 1 x 10-12 W / m 2 .
Experiências práticas para crianças
As crianças podem aprender muito sobre ondas mecânicas enquanto se divertem. Aqui estão várias experiências simples para verificar como as ondas transmitem energia, que pode ser aproveitada.
-Experimento 1: Intercomunicador
Materiais
– 2 copos de plástico cuja altura é muito maior que o diâmetro.
– Entre 5 e 10 metros de fio forte.
Implementação
Perfure a base dos vasos para passar a linha através deles e prenda-a com um nó em cada extremidade, para que a linha não saia.
– Cada jogador pega um copo e se afasta em uma linha reta, garantindo que o fio esteja esticado.
– Um dos jogadores usa o copo como microfone e fala com o parceiro, que, é claro, deve colocar o copo no ouvido para poder ouvir. Não é necessário gritar.
O ouvinte perceberá imediatamente que o som da voz de seu parceiro é transmitido através do fio tenso. Se o fio não estiver esticado, a voz do seu amigo não será ouvida com clareza. Tampouco se ouvirá nada se o fio for colocado diretamente no ouvido, é necessário ouvir o copo.
Explicação
Sabemos pelas seções anteriores que a tensão na corda afeta a velocidade da onda. A transmissão também depende do material e do diâmetro dos vasos. Quando o parceiro fala, a energia de sua voz é transmitida ao ar (onda longitudinal), de lá para o fundo do vaso e depois como uma onda transversal através do fio.
O fio transmite a onda para o fundo do vaso do ouvinte, que vibra. Essa vibração é transmitida ao ar e é percebida pelo tímpano e interpretada pelo cérebro.
Experiência 2: Observando as ondas
Implementação
Sobre uma mesa ou superfície plana encontra-se um colante , a mola helicoidal flexível com os quais podem formar vários tipos de onda.

Ondas longitudinais
As extremidades são seguradas, uma em cada mão. Em seguida, um pequeno impulso horizontal é aplicado em uma das extremidades e é observado como um pulso se propaga ao longo da mola.
Você também pode colocar uma extremidade do furtivo fixo em algum suporte ou pedir a um parceiro para segurá-lo, esticando-o o suficiente. Dessa forma, há mais tempo para observar como as compressões e expansões ocorrem, espalhando-se de uma extremidade do píer para a outra rapidamente, conforme descrito nas seções anteriores.
Ondas transversais
O slinky também é segurado por uma de suas extremidades, esticando-o suficientemente. A extremidade livre é levemente abalada agitando-a para cima e para baixo. Observa-se que o pulso sinusoidal se move ao longo da mola e retorna.
Referências
- Giancoli, D. (2006). Física: Princípios com aplicações. Sexta Edição Prentice Hall. 308- 336.
- Hewitt, Paul. (2012). Ciência Física Conceitual. Quinta Edição Pearson 239-244.
- Rex, A. (2011). Fundamentos de Física. Pearson 263-273.