O princípio de Pascal é uma lei da física que descreve a transmissão de pressão em um fluido confinado. Foi formulado pelo matemático e físico francês Blaise Pascal no século XVII. O princípio de Pascal tem diversas aplicações práticas, sendo fundamental em áreas como engenharia, hidráulica e mecânica. Um exemplo clássico que ilustra o princípio de Pascal é o elevador hidráulico, onde a pressão exercida em um ponto de um fluido é transmitida de maneira igual e em todas as direções. Este princípio é essencial para o funcionamento de diversos dispositivos e máquinas que utilizam fluidos para transmitir força e movimento.
Descubra as diferentes maneiras de aplicar o Princípio de Pascal em diversas situações.
O Princípio de Pascal, formulado pelo físico e matemático Blaise Pascal no século XVII, é uma lei da física que descreve a transmissão de pressão em um fluido confinado. De acordo com esse princípio, a pressão aplicada em um ponto de um fluido confinado é transmitida igualmente em todas as direções, podendo ser utilizado em diversas situações do dia a dia.
Uma das aplicações mais comuns do Princípio de Pascal é no funcionamento dos sistemas hidráulicos, como freios de carros e elevadores. Nestes sistemas, a pressão exercida em um ponto do fluido é transmitida para todos os outros pontos, permitindo a multiplicação da força aplicada. Isso é fundamental para a operação eficiente desses equipamentos.
Além disso, o Princípio de Pascal também pode ser observado em situações cotidianas, como ao espremer uma pasta de dente. Quando pressionamos a embalagem, a pressão aplicada é transmitida para o fluido dentro dela, fazendo com que a pasta saia pela abertura. Isso ocorre porque a pressão se propaga igualmente em todas as direções.
Outro exemplo de aplicação do Princípio de Pascal é a prensa hidráulica, utilizada na indústria para moldar peças metálicas. Nesse caso, a pressão aplicada em um dos pistões é transmitida para o outro, permitindo a realização de trabalhos de alta precisão.
Seja na indústria, no transporte ou mesmo em atividades do dia a dia, a compreensão desse princípio pode facilitar a resolução de problemas e a criação de soluções inovadoras.
Os fatores que influenciam a Lei de Pascal.
O Princípio de Pascal, também conhecido como Lei de Pascal, foi enunciado pelo físico e matemático francês Blaise Pascal no século XVII. Basicamente, a lei afirma que em um fluido em equilíbrio, qualquer variação de pressão aplicada em um ponto do fluido se transmite igualmente para todos os pontos do mesmo fluido.
Existem diversos fatores que influenciam a Lei de Pascal. O principal deles é a pressão. Quanto maior a pressão aplicada em um ponto do fluido, maior será a pressão transmitida para os demais pontos. Além disso, a densidade do fluido também é um fator importante. Fluidos com maior densidade tendem a transmitir a pressão de forma mais eficiente.
Outro fator relevante é a forma do recipiente que contém o fluido. Recipientes com formatos diferentes podem influenciar a distribuição da pressão no fluido. Além disso, a gravidade também pode influenciar a Lei de Pascal, uma vez que a pressão em um fluido pode variar de acordo com a aceleração da gravidade no local.
O Princípio de Pascal tem diversas aplicações práticas, sendo muito utilizado em sistemas hidráulicos, como freios de carros e elevadores hidráulicos. Um exemplo simples de aplicação da Lei de Pascal é o funcionamento de uma prensa hidráulica. Ao se aplicar uma pequena força em um pistão menor, a pressão gerada é transmitida para um pistão maior, permitindo a realização de trabalhos que exigiriam uma força muito maior.
Autor do Princípio de Pascal: quem foi o responsável por sua formulação?
O Princípio de Pascal é uma lei da física que descreve o funcionamento dos fluidos em equilíbrio. Foi formulado pelo matemático e físico francês Blaise Pascal no século XVII. Pascal, que também é conhecido por suas contribuições para a matemática e filosofia, enunciou esse princípio em seu trabalho “Experiences nouvelles touchant le vide” em 1647.
O Princípio de Pascal afirma que “a pressão exercida em um ponto de um fluido em equilíbrio distribui-se igualmente por todo o fluido”. Isso significa que qualquer variação de pressão aplicada a um fluido confinado será transmitida igualmente em todas as direções.
As aplicações do Princípio de Pascal são diversas e estão presentes em várias áreas do conhecimento, como na engenharia, na medicina e na indústria. Um exemplo clássico é o funcionamento de sistemas hidráulicos, nos quais a pressão exercida em um ponto é transmitida através de um fluido para outro ponto.
Outro exemplo prático do Princípio de Pascal é o funcionamento das prensas hidráulicas, que utilizam a multiplicação da força através da transmissão de pressão para realizar tarefas como a compressão de materiais.
Aprenda a calcular a Lei de Pascal de forma simples e eficiente.
O Princípio de Pascal, criado pelo físico e matemático Blaise Pascal no século XVII, é uma lei fundamental da física que descreve como a pressão aplicada em um ponto de um fluido em repouso é transmitida igualmente em todas as direções. Isso significa que qualquer alteração na pressão de um fluido em um ponto de um recipiente se propaga por todo o fluido de forma uniforme.
Para calcular a Lei de Pascal, basta usar a fórmula matemática P1 x A1 = P2 x A2, onde P1 é a pressão inicial, A1 é a área inicial, P2 é a pressão final e A2 é a área final. Essa fórmula simples permite determinar como a pressão aplicada em um ponto de um fluido se distribui pelo restante do fluido.
O Princípio de Pascal tem diversas aplicações práticas, sendo muito utilizado em sistemas hidráulicos, como freios de carros e elevadores hidráulicos. Além disso, ele também é fundamental em áreas como medicina, engenharia e arquitetura, onde a transmissão de pressão é essencial para o funcionamento de diversos dispositivos e estruturas.
Um exemplo clássico da Lei de Pascal é o funcionamento de um macaco hidráulico. Quando uma força é aplicada em um dos pistões, a pressão é transmitida pelo fluido e eleva o outro pistão de forma proporcional, permitindo levantar carros e objetos pesados com facilidade.
Agora que você entendeu a importância e as aplicações do Princípio de Pascal, experimente calcular a Lei de Pascal em diferentes situações e veja como a pressão se distribui de forma igual por todo o fluido. Com um pouco de prática, você estará dominando esse conceito fundamental da física de maneira simples e eficiente.
Princípio de Pascal: história, aplicações, exemplos
O princípio da Pascal , Pascal ou lei estabelece que uma mudança na pressão de um fluido confinado em qualquer ponto é transmitida inalterada para todos os outros pontos dentro do fluido.
Este princípio foi descoberto pelo cientista francês Blaise Pascal (1623-1662). Devido à importância das contribuições de Pascal à ciência, a unidade de pressão no Sistema Internacional foi nomeada em sua homenagem.

Como a pressão é definida como a razão entre a força perpendicular a uma superfície entre sua área, 1 Pascal (Pa) é igual a 1 newton / m 2 .
História
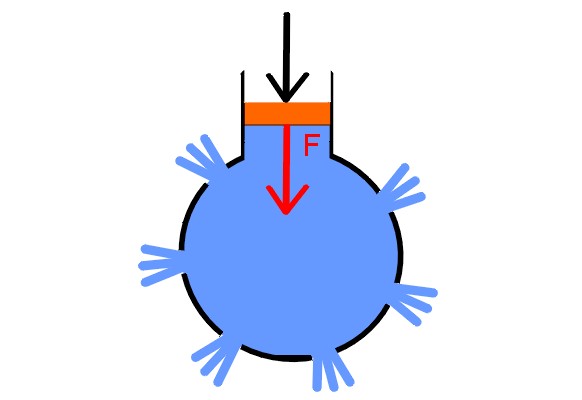
Para provar seu princípio, Pascal planejou uma demonstração bastante contundente. Ele pegou uma esfera oca e furada em vários lugares, colocou plugues em todos os buracos, exceto um, através do qual ele a encheu de água. Nisto, ele colocou uma seringa fornecida com um êmbolo.
Ao aumentar suficientemente a pressão no pistão, os bujões são acionados ao mesmo tempo, porque a pressão é transmitida igualmente a todos os pontos do fluido e em todas as direções, demonstrando a lei de Pascal.
Blaise Pascal teve uma vida curta, marcada pela doença. O incrível alcance de sua mente o levou a investigar vários aspectos da natureza e da filosofia. Suas contribuições não se limitaram ao estudo do comportamento de fluidos, Pascal também foi pioneiro na computação.
E com 19 anos de idade, Pascal criou uma calculadora mecânica para seu pai usar em seu trabalho no sistema tributário francês: a pascalina .
Além disso, juntamente com seu amigo e colega, o grande matemático Pierre de Fermat, eles moldaram a teoria das probabilidades, indispensável em Física e Estatística. Pascal faleceu em Paris aos 39 anos.
Explicação do princípio de Pascal
O experimento a seguir é bastante simples: um tubo em U é preenchido com água e são colocados tampões em cada extremidade que podem deslizar suave e facilmente, como um pistão. A pressão é pressionada contra o pistão esquerdo afundando-o um pouco e observa-se que o da direita sobe, empurrado pelo fluido (figura 3).

Isso acontece porque a pressão é transmitida sem qualquer diminuição em qualquer ponto do fluido, incluindo aqueles em contato com o pistão direito.
Líquidos como água ou óleo são incompressíveis, mas ao mesmo tempo as moléculas têm liberdade de movimento suficiente, o que possibilita a distribuição da pressão no pistão direito.
Graças a isso, o pistão direito recebe uma força exatamente igual em magnitude e direção à qual foi aplicado à esquerda, mas na direção oposta.
A pressão em um fluido estático é independente da forma do recipiente. Será demonstrado imediatamente que a pressão varia linearmente com a profundidade e o princípio de Pascal é uma conseqüência disso.
Uma alteração da pressão em qualquer ponto faz com que a pressão em outro ponto seja alterada na mesma quantidade. Caso contrário, haveria uma pressão extra que fluiria o líquido.
A relação entre pressão e profundidade
Um fluido em repouso exerce uma força nas paredes do recipiente que o contém e também na superfície de qualquer objeto submerso nele. No experimento da seringa de Pascal, observa-se que os filetes de água saem perpendicularmente à esfera.
Fluidos força distribuídas perpendicularmente sobre a superfície em que ele actua, por isso, é desejável para introduzir o conceito de média pressão P m e a força exercida perpendicularmente F ⊥ por área A , a unidade de SI é pascal:
P m = F ⊥ / A
A pressão aumenta com a profundidade. Pode ser visto isolando uma pequena porção de fluido em equilíbrio estático e aplicando a segunda lei de Newton:
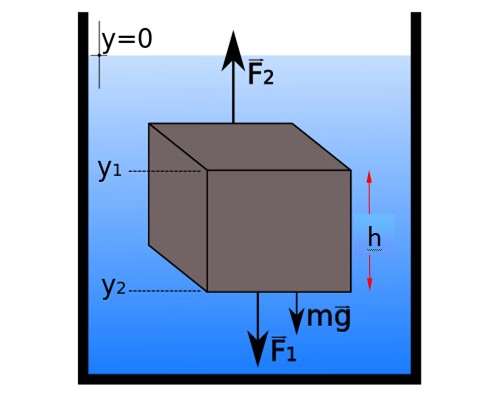
As forças horizontais são canceladas em pares, mas na direção vertical, as forças são agrupadas da seguinte forma:
∑F y = F 2 – F 1 – mg = 0 → F 2 – F 1 = mg
Expressando massa em termos de densidade ρ = massa / volume:
P 2 .A- P 1 .A = ρ x volume xg
O volume da porção de fluido é o produto A xh:
A. (P 2 – P 1 ) = ρ x A xhxg
ΔP = ρ .gh Teorema fundamental da hidrostática
Aplicações
O princípio de Pascal foi usado para construir inúmeros dispositivos que multiplicam a força e facilitam tarefas como levantar pesos, estampar metais ou pressionar objetos. Entre eles estão:
-A prensa hidráulica
-O sistema de freio do carro
-Pás mecânicas e braços mecânicos
-O macaco hidráulico
-Camiões e elevadores
A seguir, vamos ver como o princípio de Pascal faz com que pequenas forças se tornem grandes forças para executar todos esses trabalhos. A prensa hidráulica é o exemplo mais característico e será analisada abaixo.
Prensa hidráulica
Para construir uma prensa hidráulica, é utilizado o mesmo dispositivo da figura 3, ou seja, um recipiente em forma de U, do qual já sabemos que a mesma força é transmitida de um pistão para outro. A diferença será o tamanho dos pistões e é isso que faz o dispositivo funcionar.
A figura a seguir mostra o princípio de Pascal em ação. A pressão é a mesma em todos os pontos do fluido, tanto nos pistões pequenos quanto nos grandes:
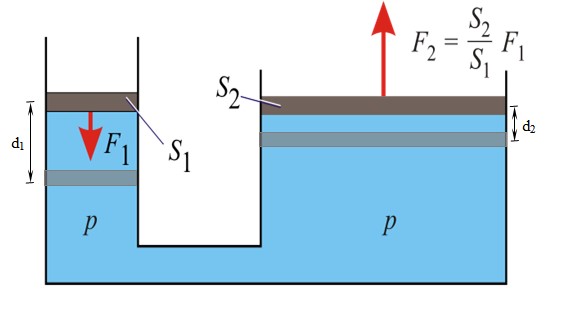
p = F 1 / S 1 = F 2 / S 2
A magnitude da força transmitida ao pistão grande é:
F 2 = (S 2 / S 1 ). F 1
Como S 2 > S 1 , resulta em F 2 > F 1 , portanto a força de saída multiplicou-se pelo fator dado pela razão entre as áreas.
Exemplos
Esta seção apresenta exemplos de aplicação.
Freios hidráulicos
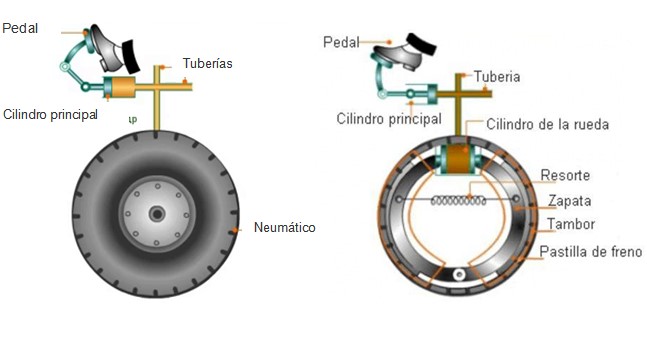
Os freios de carro fazem uso do princípio de Pascal através de um fluido hidráulico que enche os tubos conectados às rodas. Quando ele precisa parar, o motorista aplica uma força pressionando o pedal do freio e gerando uma pressão no fluido.
Na outra extremidade, a pressão empurra as pastilhas de freio contra o tambor ou os discos de freio que giram em conjunto com as rodas (não com os pneus). O atrito resultante faz com que o disco pare, diminuindo a velocidade das rodas.
Vantagem mecânica da prensa hidráulica
Na prensa hidráulica da Figura 5, o trabalho de entrada deve ser igual ao trabalho de saída, desde que o atrito não seja levado em consideração.
A força de entrada F 1 faz com que o pistão percorra uma distância d 1 ao abaixar, enquanto a força de saída F 2 permite um deslocamento d 2 do pistão que sobe. Se o trabalho mecânico realizado por ambas as forças for o mesmo:
F 1 .d 1 = F 2 . d 2
A vantagem mecânica M é a razão entre as magnitudes da força de entrada e saída:
M = F 2 / F 1 = d 1 / d 2
E, como demonstrado na seção anterior, também pode ser expressa como a razão entre as áreas:
F 2 / F 1 = S 2 / S 1
Parece que é possível realizar um trabalho livre, mas, na verdade, nenhuma energia está sendo criada com este dispositivo, uma vez que a vantagem mecânica é obtida às custas do deslocamento do pistão pequeno d 1 .
Portanto, para otimizar o desempenho, um sistema de válvulas é adicionado ao dispositivo de forma que o pistão de saída suba graças a pulsos curtos no pistão de entrada.
Desta forma, o operador de um macaco hidráulico de garagem bombeia várias vezes para levantar gradualmente um veículo.
Exercício resolvido
Na prensa hidráulica da Figura 5, as áreas dos pistões são de 0,5 polegadas quadradas (pistão pequeno) e 25 polegadas quadradas (pistão grande). Localizar:
a) A vantagem mecânica desta impressora.
b) A força necessária para elevar uma carga de 1 tonelada.
c) A distância na qual a força de entrada deve atuar para elevar a referida carga em 1 polegada.
Expresse todos os resultados em unidades do sistema britânico e do Sistema Internacional SI.
Solução
a) A vantagem mecânica é:
M = F 2 / F 1 = S 2 / S 1 = 25 em 2 / 0,5 em 2 = 50
b) 1 tonelada é igual a 2000 lb-força. A força necessária é F 1 :
F 1 = F 2 / M = 2000 lb-força / 50 = 40 lb-força
Para expressar o resultado no Sistema Internacional, é necessário o seguinte fator de conversão:
1 lb-força = 4,448 N
Portanto, a magnitude de F1 é 177,92 N.
c) M = d 1 / d 2 → d 1 = Md 2 = 50 x 1 in = 50 in
O fator de conversão necessário é: 1 in = 2,54 cm
d 1 = 127 cm = 1,27 m
Referências
- Bauer, W. 2011. Física para Engenharia e Ciência. Volume 1. Mc Graw Hill. 417-450.
- Física Física Princípio de Pascal. Recuperado de: opentextbc.ca.
- Figueroa, D. (2005). Série: Física para Ciência e Engenharia. Volume 4. Fluidos e Termodinâmica. Editado por Douglas Figueroa (USB). 4-12.
- Rex, A. 2011. Fundamentos de Física. Pearson 246-255.
- Tippens, P. 2011. Física: Conceitos e Aplicações. 7ª Edição. McGraw Hill, 301-320.