O método dos quadrados mínimos é uma técnica utilizada na estatística e na matemática para encontrar a melhor aproximação linear de um conjunto de pontos dispersos. Este método consiste em minimizar a soma dos quadrados das diferenças entre os valores observados e os valores preditos por uma função linear.
Neste contexto, os exercícios de quadrados mínimos são comuns em cursos de estatística, matemática e engenharias, pois ajudam a compreender como encontrar a melhor reta de ajuste para um conjunto de dados e como calcular os coeficientes de regressão.
O método dos quadrados mínimos é amplamente utilizado em áreas como econometria, análise de dados, previsão de séries temporais, entre outras, pois permite estimar os parâmetros de um modelo matemático de forma precisa e eficiente. Em resumo, o método dos quadrados mínimos é uma ferramenta poderosa para modelar relações entre variáveis e fazer previsões com base em dados observados.
Qual a utilidade do método dos mínimos quadrados na análise estatística de dados?
O método dos mínimos quadrados é uma técnica amplamente utilizada na análise estatística de dados. Ele consiste em encontrar a “melhor” reta que se ajusta aos pontos de um conjunto de dados, minimizando a soma dos quadrados das diferenças entre os valores observados e os valores previstos pela reta.
Essa técnica é muito útil em diversas áreas, como na física, na economia, na engenharia e em muitas outras. Ela permite realizar previsões e estimativas com base nos dados disponíveis, além de identificar padrões e tendências nos dados observados.
Com o método dos mínimos quadrados, é possível realizar análises mais precisas e confiáveis, tornando-o uma ferramenta essencial para os profissionais que lidam com dados e estatísticas. Ele também é muito utilizado em pesquisas acadêmicas e em estudos científicos, contribuindo para a obtenção de resultados mais robustos e significativos.
Portanto, a utilização do método dos mínimos quadrados na análise estatística de dados é fundamental para a obtenção de insights valiosos e para a tomada de decisões embasadas em informações concretas e confiáveis.
A importância da utilização do Método dos Mínimos Quadrados na Inteligência Artificial.
O Método dos Mínimos Quadrados é uma técnica estatística amplamente utilizada em diversos campos, incluindo a Inteligência Artificial. Este método é fundamental para estimar os parâmetros de um modelo matemático a partir de um conjunto de dados observados. Ao minimizar a soma dos quadrados das diferenças entre os valores observados e os valores previstos pelo modelo, o Método dos Mínimos Quadrados permite encontrar a melhor aproximação para os dados disponíveis.
Na área da Inteligência Artificial, a utilização deste método é essencial para o desenvolvimento de algoritmos de aprendizado de máquina e para a construção de modelos preditivos. Através da aplicação do Método dos Mínimos Quadrados, os pesquisadores e engenheiros podem ajustar os parâmetros de um modelo de forma a minimizar o erro de predição e melhorar a precisão das previsões.
Além disso, o Método dos Mínimos Quadrados é utilizado em problemas de otimização, reconstrução de imagens, filtragem de sinais, entre outras aplicações em Inteligência Artificial. Sua simplicidade e eficácia tornam-no uma ferramenta poderosa para a análise e interpretação de dados em diversos contextos.
Em resumo, a utilização do Método dos Mínimos Quadrados na Inteligência Artificial é fundamental para a construção de modelos mais precisos e para a melhoria do desempenho dos sistemas de IA. Portanto, é importante que os profissionais da área estejam familiarizados com esta técnica e saibam como aplicá-la de forma eficaz em seus projetos.
Origem do método dos mínimos quadrados: descubra quem foi o responsável por sua criação.
O método dos mínimos quadrados é uma técnica estatística utilizada para encontrar a melhor linha de ajuste para um conjunto de dados. Ele foi desenvolvido pelo matemático francês Adrien-Marie Legendre no final do século XVIII. A ideia por trás do método é minimizar a soma dos quadrados das diferenças entre os valores observados e os valores preditos pela linha de regressão.
Legendre foi o responsável por formalizar matematicamente o método dos mínimos quadrados e demonstrar sua utilidade em diversos campos, como na física e na astronomia. Hoje em dia, o método dos mínimos quadrados é amplamente utilizado em diversas áreas, como na economia, na engenharia e na biologia, para analisar dados e fazer previsões.
Para aplicar o método dos mínimos quadrados, é necessário calcular as derivadas parciais das equações de erro em relação aos parâmetros desconhecidos, igualá-las a zero e resolver o sistema de equações resultante. O resultado é a estimativa dos parâmetros que melhor se ajustam aos dados observados.
Em resumo, o método dos mínimos quadrados é uma ferramenta poderosa para encontrar a melhor aproximação linear para um conjunto de dados, permitindo fazer previsões e inferências com base em informações observadas.
Entendendo o conceito de modelo de regressão linear na análise estatística de dados.
Em análise estatística de dados, o modelo de regressão linear é uma ferramenta importante para entender a relação entre uma variável dependente e uma ou mais variáveis independentes. Neste modelo, busca-se encontrar uma equação que represente a relação linear entre as variáveis, permitindo fazer previsões e inferências com base nos dados observados.
O método dos Quadrados Mínimos é uma técnica comumente utilizada para estimar os parâmetros do modelo de regressão linear. Ele consiste em minimizar a soma dos quadrados das diferenças entre os valores observados e os valores estimados pelo modelo. Dessa forma, obtém-se uma linha de melhor ajuste que representa a relação entre as variáveis de forma mais precisa.
Para realizar o cálculo dos coeficientes do modelo de regressão linear utilizando o método dos Quadrados Mínimos, é necessário resolver um sistema de equações lineares. Esse processo envolve encontrar os valores dos coeficientes que minimizam a soma dos quadrados dos resíduos, ou seja, a diferença entre os valores observados e os valores estimados pelo modelo.
O método dos Quadrados Mínimos é amplamente utilizado em diversas áreas, como economia, engenharia, ciências sociais e muitas outras. Ele permite analisar e interpretar a relação entre variáveis quantitativas, fazer previsões e tomar decisões com base nos dados disponíveis.
Em resumo, o modelo de regressão linear em conjunto com o método dos Quadrados Mínimos é uma poderosa ferramenta para analisar e interpretar dados, identificar padrões e fazer previsões com base em relações lineares entre variáveis. É essencial para a tomada de decisões fundamentadas em evidências e para o avanço do conhecimento em diversas áreas do conhecimento.
Quadrados mínimos: método, exercícios e para que serve
O método dos mínimos quadrados é uma das aplicações mais importantes na aproximação de funções. A idéia é encontrar uma curva tal que, dado um conjunto de pares ordenados, essa função esteja mais próxima dos dados. A função pode ser uma linha, uma curva quadrática, uma cúbica, etc.
A idéia do método é minimizar a soma dos quadrados das diferenças nas ordenadas (componente Y), entre os pontos gerados pela função escolhida e os pontos pertencentes ao conjunto de dados.
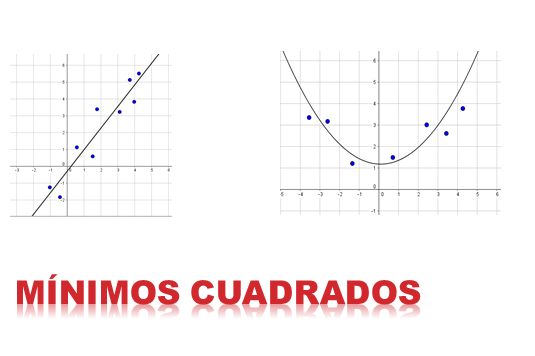
Método dos mínimos quadrados
Antes de dar o método, devemos primeiro esclarecer o que significa “aproximar-se”. Suponha que você esteja procurando uma linha y = b + mx que melhor represente um conjunto de n pontos, a saber {(x1, y1), (x2, y2) …, (xn, yn)}.
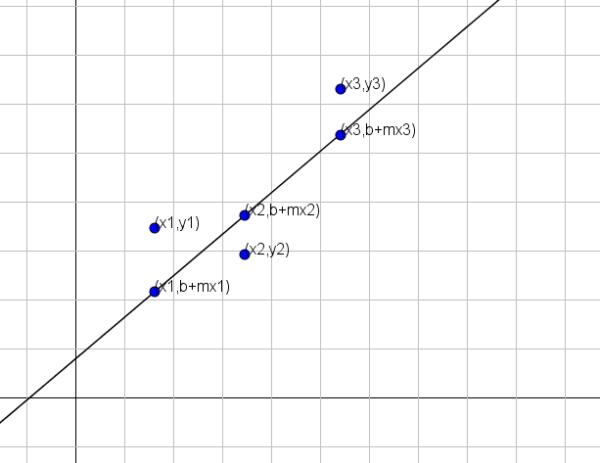
Conforme mostrado na figura anterior, se as variáveis xyy fossem relacionadas pela linha y = b + mx, então para x = x1 o valor correspondente de y seria b + mx1. No entanto, esse valor é diferente do valor verdadeiro de y, que é y = y1.
Lembre-se de que, no plano, a distância entre dois pontos é dada pela seguinte fórmula:

Com isso em mente, para determinar como escolher a linha y = b + mx que melhor se aproxima dos dados fornecidos, parece lógico usar como critério a seleção da linha que minimiza a soma dos quadrados das distâncias entre os pontos e a reta
Como a distância entre os pontos (x1, y1) e (x1, b + mx1) é y1- (b + mx1), nosso problema é reduzido para encontrar números myb, de modo que a seguinte soma seja mínima:
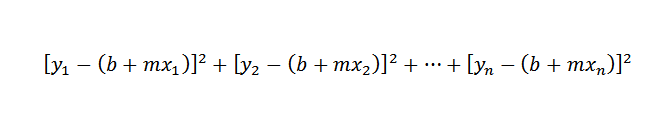
A linha que atende a essa condição é conhecida como “aproximação da linha dos mínimos quadrados aos pontos (x1, y1), (x2, y2), …, (xn, yn)”.
Uma vez que o problema é obtido, é necessário apenas escolher um método para encontrar a aproximação por mínimos quadrados. Se os pontos (x1, y1), (x2, y2), …, (xn, yn) estiverem todos na linha y = mx + b, teríamos que ser colineares e:

Nesta expressão:

Finalmente, se os pontos não são colineares, então y-Au = 0 e o problema pode ser traduzido em encontrar um vetor ou tal que a norma euclidiana seja mínima.

Encontrar o vetor minimizador não é tão difícil quanto se poderia pensar. Como A é uma matriz nx2 e u é uma matriz 2 × 1, temos que o vetor Au é um vetor em R n e pertence à imagem de A, que é um subespaço de R n com uma dimensão não superior a duas.
Vamos assumir que n = 3 para mostrar qual procedimento deve ser seguido. Se n = 3, a imagem de A será um plano ou uma linha que passa pela origem.
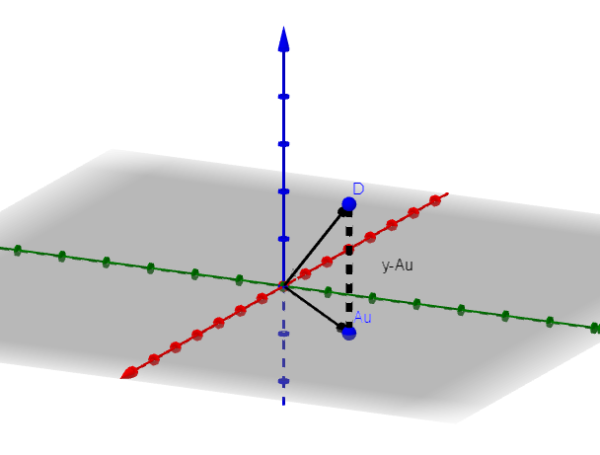
Seja v o vetor minimizador. Na figura, observamos que y-Au é minimizado quando ortogonal à imagem de A. Ou seja, se v é o vetor minimizador, acontece que:

Então, podemos expressar o exposto desta maneira:

Isso só pode acontecer se:

Finalmente, limpando v, temos que:

É possível fazer isso, já que A t A é invertível desde que os n pontos dados como dados não sejam colineares.
Agora, se, em vez de procurar uma linha, desejássemos encontrar uma parábola (cuja expressão seria da forma y = a + bx + cx 2 ) que fosse uma melhor aproximação aos n pontos de dados, o procedimento seria o descrito abaixo.
Se os n pontos de dados estivessem na referida parábola, seria necessário:

Então:

Da mesma forma, podemos escrever y = Au. Se todos os pontos não estão na parábola, temos que y-Au é diferente de zero para qualquer vetor u e nosso problema é novamente: encontre um vetor u em R3 de modo que sua norma || y-Au || Seja o menor possível.
Repetindo o procedimento anterior, podemos chegar ao vetor desejado é:

Exercícios resolvidos
Exercício 1
Encontre a linha que melhor se ajusta aos pontos (1.4), (-2.5), (3, -1) e (4.1).
Solução
Temos que:

Então:
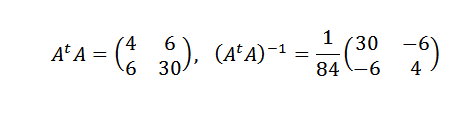

Portanto, concluímos que a linha que melhor se ajusta aos pontos é dada por:

Exercício 2
Suponha que um objeto caia de uma altura de 200 m. Enquanto cai, são tomadas as seguintes medidas:

Sabemos que a altura do referido objeto, depois de decorrido um tempo t, é dada por:

Se quisermos obter o valor de g, podemos procurar uma parábola que seja uma melhor aproximação aos cinco pontos dados na tabela e, portanto, teríamos que o coeficiente que acompanha 2 seja uma aproximação razoável de (-1/2) g se o As medições são precisas.
Temos que:

E logo:
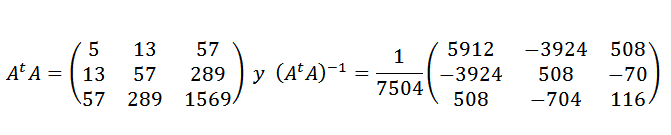

Portanto, os pontos de dados são ajustados pela seguinte expressão quadrática:

Então, você precisa:
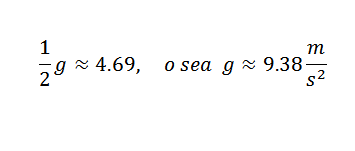
Este é um valor razoavelmente próximo do correto, que é g = 9,81 m / s 2 . Para obter uma aproximação mais precisa de g, seria necessário começar com observações mais precisas.
Para que serve?
Nos problemas que ocorrem nas ciências naturais ou sociais, é conveniente escrever as relações que existem entre diferentes variáveis através de alguma expressão matemática.
Por exemplo, podemos relacionar economicamente custo (C), renda (I) e lucros (U) por meio de uma fórmula simples:
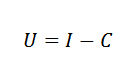
Em física, podemos relacionar a aceleração causada pela gravidade, o tempo em que um objeto está caindo e a altura do objeto por lei:

Na expressão anterior, s o é a altura inicial do referido objeto e v o é a sua velocidade inicial.
No entanto, encontrar fórmulas como essas não é uma tarefa simples; De maneira geral, cabe ao profissional de serviço trabalhar com muitos dados e realizar várias experiências repetidamente (para verificar se os resultados obtidos são constantes) para encontrar relações entre os diferentes dados.
Uma maneira comum de conseguir isso é representar os dados obtidos em um plano como pontos e procurar uma função contínua que se aproxime otimamente desses pontos.
Uma das maneiras de encontrar a função que “melhor se aproxima” dos dados fornecidos é pelo método dos mínimos quadrados.
Além disso, como também vimos no exercício, graças a esse método, podemos obter aproximações bastante próximas das constantes físicas.
Referências
- Álgebra linear de Charles W Curtis. Springer-velarg
- Kai Lai Chung Teoria Elementar da Probabilidade com Processos Estocásticos. Springer-Verlag Nova Iorque Inc
- Richar L Burden e J. Douglas Faires. Análise Numérica (7ed). Thompson Learning
- Stanley I. Grossman. Aplicações de álgebra linear. MCGRAW-HILL / INTERAMERICANO DE MÉXICO
- Stanley I. Grossman. Álgebra Linear. MCGRAW-HILL / INTERAMERICANO DE MÉXICO