O módulo de cisalhamento, também conhecido como rigidez ou cisalhamento, é uma propriedade mecânica de um material que mede sua capacidade de resistir a forças de cisalhamento, ou seja, aquelas que atuam perpendicularmente à direção de aplicação da força. Este parâmetro é fundamental para o dimensionamento de estruturas e materiais que estão sujeitos a esforços de cisalhamento.
Neste artigo, apresentaremos uma série de exercícios resolvidos que abordam o cálculo do módulo de cisalhamento em diferentes materiais e situações. Com esses exemplos práticos, será possível compreender melhor como essa propriedade é determinada e sua importância na engenharia e na mecânica dos materiais.
Descubra a forma correta de calcular o módulo de cisalhamento de materiais.
O módulo de cisalhamento, também conhecido como rigidez ou cisalhamento, é uma propriedade importante dos materiais que descreve a capacidade de um material de resistir a forças de cisalhamento. Para calcular o módulo de cisalhamento de um material, é necessário considerar a relação entre a tensão de cisalhamento e a deformação de cisalhamento.
A fórmula para calcular o módulo de cisalhamento é dada por:
G = τ / γ
Onde:
- G é o módulo de cisalhamento
- τ é a tensão de cisalhamento
- γ é a deformação de cisalhamento
Para calcular o módulo de cisalhamento, é necessário conhecer a tensão de cisalhamento aplicada ao material e a deformação resultante. Com esses valores, é possível determinar a rigidez do material em resposta às forças de cisalhamento.
Para exemplificar, vamos resolver um exercício:
Se uma amostra de material sofre uma tensão de cisalhamento de 50 MPa e uma deformação de cisalhamento de 0,02, qual é o módulo de cisalhamento do material?
Substituindo os valores na fórmula, temos:
G = 50 MPa / 0,02 = 2500 MPa
Portanto, o módulo de cisalhamento do material é de 2500 MPa.
É importante ressaltar que o módulo de cisalhamento é uma propriedade fundamental para a análise e o projeto de estruturas, sendo essencial para garantir a resistência e a estabilidade dos materiais em diversas aplicações.
Métodos eficazes para calcular o cisalhamento em estruturas de forma precisa e confiável.
O módulo de cisalhamento, também conhecido como rigidez de cisalhamento, é uma propriedade importante para o cálculo de esforços em estruturas. Para calcular o cisalhamento de forma precisa e confiável, é essencial utilizar métodos adequados que levem em consideração as características da estrutura e as cargas aplicadas.
Um dos métodos mais eficazes para calcular o cisalhamento em estruturas é o método dos elementos finitos. Este método consiste em dividir a estrutura em elementos menores, nos quais são aplicadas equações de equilíbrio e comportamento dos materiais para determinar as tensões e deformações em cada ponto da estrutura. O uso de software especializado pode facilitar o processo e fornecer resultados precisos.
Outro método comumente utilizado para calcular o cisalhamento é o método analítico, que envolve o uso de equações matemáticas para determinar as forças internas na estrutura. Este método requer um conhecimento sólido de mecânica dos materiais e resistência dos materiais, mas pode ser muito preciso se aplicado corretamente.
Além disso, é importante considerar as condições de contorno da estrutura, como apoios e restrições, para garantir a precisão dos cálculos de cisalhamento. A escolha adequada de modelos de análise e a verificação dos resultados com ensaios práticos também são essenciais para garantir a confiabilidade dos cálculos.
Com a aplicação correta desses métodos, é possível obter resultados precisos e confiáveis para o dimensionamento e análise de estruturas.
Cálculo do módulo de elasticidade: passo a passo para determinar a resistência dos materiais.
O módulo de elasticidade, também conhecido como módulo de Young, é uma medida da rigidez de um material. Ele representa a capacidade do material de suportar deformações elásticas sob a ação de uma carga externa. Para calcular o módulo de elasticidade de um material, é necessário realizar um teste de tração, onde a amostra é submetida a uma carga crescente até a ruptura.
O cálculo do módulo de elasticidade é feito utilizando a fórmula E = σ/ε, onde E representa o módulo de elasticidade, σ é a tensão aplicada e ε é a deformação sofrida pelo material. Para determinar o valor do módulo de elasticidade, é necessário plotar um gráfico do esforço aplicado em função da deformação e calcular a inclinação da reta resultante. Esta inclinação corresponde ao módulo de elasticidade do material.
Por outro lado, o módulo de cisalhamento, também conhecido como módulo de rigidez ou de cisalhamento, é uma medida da resistência de um material à deformação por cisalhamento. Ele é representado pela letra G e é utilizado para calcular a deformação angular sofrida por um material sob a ação de uma força tangencial.
Para determinar o módulo de cisalhamento de um material, é necessário realizar um teste de cisalhamento, onde uma força tangencial é aplicada à amostra. O cálculo do módulo de cisalhamento é feito utilizando a fórmula G = τ/γ, onde G representa o módulo de cisalhamento, τ é a tensão de cisalhamento aplicada e γ é a deformação angular sofrida pelo material.
Ambos os parâmetros são essenciais para a determinação das propriedades mecânicas dos materiais e são amplamente utilizados na engenharia e na indústria.
Qual é a força de corte necessária para romper um material?
Para entender a força de corte necessária para romper um material, é importante conhecer o conceito de módulo de cisalhamento, também conhecido como rigidez ou cisalhamento. O módulo de cisalhamento é uma medida da resistência de um material à deformação por cisalhamento, ou seja, a tendência do material a se deformar quando sujeito a forças de corte.
O módulo de cisalhamento é representado pela letra G e é uma propriedade fundamental de um material. Ele está relacionado à resistência do material à deformação por cisalhamento e é essencial para determinar a força de corte necessária para romper o material.
Para calcular a força de corte necessária para romper um material, é preciso levar em consideração o módulo de cisalhamento do material, juntamente com outras propriedades mecânicas, como a área da seção transversal do material e o comprimento sobre o qual a força de corte será aplicada.
Uma fórmula comum para calcular a força de corte necessária é a seguinte:
F = G * A * L
Onde F representa a força de corte necessária, G é o módulo de cisalhamento do material, A é a área da seção transversal do material e L é o comprimento sobre o qual a força de corte será aplicada.
Portanto, o módulo de cisalhamento é uma propriedade importante para determinar a resistência de um material à deformação por cisalhamento e para calcular a força de corte necessária para romper o material.
Qual é o módulo de cisalhamento, rigidez ou cisalhamento? (Exercícios resolvidos)
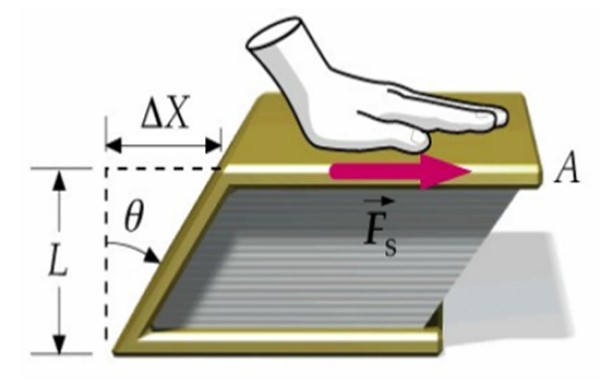
O módulo de corte descreve a resposta de um material à aplicação de uma tensão de cisalhamento que o deforma. Outras designações freqüentemente usadas para o módulo de cisalhamento são cisalhamento, cisalhamento, elasticidade transversal ou módulo de elasticidade tangencial.
Quando as tensões são pequenas, as deformações são proporcionais a elas, de acordo com a lei de Hooke, sendo o módulo de cisalhamento a constante da proporcionalidade. Portanto:
Módulo de cisalhamento = tensão de cisalhamento / urdidura
Suponha que uma força seja aplicada à capa de um livro, a outra sendo fixada na superfície da mesa. Dessa forma, o livro como um todo não se move, mas se deforma quando a capa superior se move em relação à inferior na quantidade Δx .
O livro passa de uma seção transversal retangular para uma seção de paralelogramo, como podemos ver na imagem acima.
Estar:
τ = F / A
A tensão ou tensão de cisalhamento, sendo F a magnitude da força aplicada e A a área em que atua.
A deformação causada é dada pelo quociente:
δ = Δx / L
Portanto, o módulo de corte, que designaremos como G, é:
E como Δx / L não possui dimensões, as unidades de G são as mesmas da tensão de cisalhamento, que é a razão de força por área.
No Sistema Internacional de Unidades, essas unidades são Newton / metro quadrado ou pascal, Pa abreviado. E nas unidades anglo-saxônicas, é libra / polegada quadrada, psi abreviado .
Módulo de corte para vários materiais
Sob a ação de forças de cisalhamento, como as descritas, os objetos oferecem uma resistência semelhante à do livro, na qual as camadas internas deslizam. Esse tipo de deformação pode ocorrer apenas em corpos sólidos, que possuem rigidez suficiente para se oporem à deformação.
Por outro lado, os líquidos não oferecem esse tipo de resistência, mas podem sofrer deformações de volume.
Abaixo está o módulo de corte G in Pa para vários materiais frequentemente usados na construção e na fabricação de máquinas e peças de reposição de todos os tipos:
Medição experimental do módulo de cisalhamento
Para determinar o valor do módulo de cisalhamento, amostras de cada material devem ser testadas e sua resposta à aplicação de uma tensão de cisalhamento deve ser examinada.
A amostra é uma haste feita do material, com raio conhecido R e comprimento L , que é fixado em uma extremidade, enquanto a outra é conectada ao eixo de uma polia de rotação livre.
A polia possui um cabo preso à extremidade livre, cujo peso é suspenso, o que exerce uma força F na haste através do cabo. E essa força, por sua vez, produz um momento M na haste, que gira então um pequeno ângulo θ.
Um diagrama da montagem pode ser visto na figura a seguir:
A magnitude do momento M , que denominamos M (sem negrito), está relacionada ao ângulo girado θ através do módulo de cisalhamento G, de acordo com a seguinte equação (deduzida por uma integral simples):
Como a magnitude do momento é igual ao produto do módulo de força F vezes o raio da polia R p :
M = FR p
E a força é o peso que trava W , então:
M = WR p
Substituindo na equação de magnitude do momento:
Temos a relação entre peso e ângulo:
Como encontrar o G?
Essa relação entre as variáveis W e θ é linear, de modo que os diferentes ângulos produzidos pela suspensão de diferentes pesos são medidos.
Os pares de peso e ângulo são plotados em papel milimetrado, a melhor linha que passa pelos pontos experimentais é ajustada e a inclinação m da referida linha é calculada .
Exercícios com solução
– Exercício 1
Uma haste de 2,5 metros de comprimento e raio de 4,5 mm é fixada em uma extremidade. O outro está conectado a uma polia de 75 cm de raio que tem um peso pendente W de 1,3 kg. O ângulo girado é 9,5º.
Com esses dados, é solicitado o cálculo do módulo de corte G da haste.
Solução
A partir da equação:
G é limpo:
E os valores fornecidos na declaração são substituídos, tendo o cuidado de expressar todos os dados no Sistema Internacional de Unidades da SI:
R = 4,5 mm = 4,5 x 10 -3 m
R p = 75 cm = 0,075
Para passar de quilogramas (que na verdade são quilogramas – força) para newton, multiplique por 9,8:
W = 1,3 kg-força = 1,3 x 9,8 N = 12,74 N
E, finalmente, os graus devem estar em radianos:
9,5 º = 9,5 x2π / 360 radianos = 0,1658 radianos.
Com tudo isso você tem:
= 2.237 x 10 10 Pa
– Exercício 2
Um cubo de gel mede 30 cm de lado. Uma de suas faces é fixa, mas ao mesmo tempo, uma força paralela de 1 N é aplicada à face oposta, que a desloca em 1 cm (veja o exemplo do livro na figura 1).
Você é solicitado a calcular com estes dados:
a) A magnitude da tensão de cisalhamento
b) A deformação unitária δ
c) O valor do módulo de cisalhamento
Solução para
A magnitude da tensão de cisalhamento é:
τ = F / A
Com:
A = lado 2 = (30 x 10 -2 cm) 2 = 0,09 m 2
Portanto:
τ = 1 N / 0,09 m 2 = 11,1 Pa
Solução b
A deformação unitária não é outro senão o valor de δ, dado por:
δ = Δx / L
O deslocamento da face sujeita à força é de 1 cm, então:
δ = 1/30 = 0,0333
Solução c
O módulo de cisalhamento e a razão entre a tensão de cisalhamento e a deformação da unidade:
G = tensão de cisalhamento / deformação
Portanto:
G = 11,1 Pa / 0,033 = 336,4 Pa
Referências
- Beer, F. 2010. Mecânica dos materiais. McGraw Hill. 5 ª. Edição.
- Franco García, A. Sólido rígido. Medição do módulo de cisalhamento. Recuperado de: sc.ehu.es.
- Giancoli, D. 2006. Física: Princípios com Aplicações. 6 th . Ed Prentice Hall.
- Resnick, R. (1999). Fisica. Vol. 1. 3º Ed. Em espanhol. Empresa Editorial Continental SA de CV
- Universidade de Valladolid. Departamento de Física da Matéria Condensada. Seleção de problemas. Recuperado de: www4.uva.es.