Somatório telescópico: como é resolvido e exercícios resolvidos

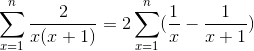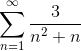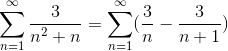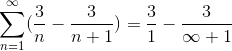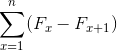
O somatório telescópico é uma técnica utilizada para simplificar a soma de uma sequência de termos que se anulam mutuamente, deixando apenas os termos extremos. Essa técnica é muito útil para simplificar expressões matemáticas e facilitar o cálculo de somas infinitas. Neste artigo, iremos explicar como o somatório telescópico é resolvido e apresentar alguns exercícios resolvidos para ajudar na compreensão e prática dessa técnica.

Descubra a soma total da série telescópica em apenas alguns passos simples.

O somatório telescópico é um tipo de série em que a maioria dos termos se cancela, restando apenas alguns para serem somados. Para resolver esse tipo de problema, basta identificar a expressão geral da série e simplificá-la até encontrar a soma total.

Para encontrar a soma total de uma série telescópica, siga estes passos simples:

Passo 1: Identifique a expressão geral da série. Por exemplo, se a série for dada por (S = 1 – frac{1}{2} + frac{1}{3} – frac{1}{4} + cdots + frac{1}{n}), a expressão geral é (S = sum_{n=1}^{N} (-1)^{n+1} frac{1}{n}).

Passo 2: Simplifique a expressão. Neste caso, agrupe os termos de forma que a maioria deles se cancele, restando apenas os primeiros e últimos termos.

Passo 3: Calcule a soma total. Neste exemplo, a soma total da série telescópica (S = 1 – frac{1}{2} + frac{1}{3} – frac{1}{4} + cdots + frac{1}{n}) pode ser encontrada substituindo (n) pelo número desejado.

Resolvendo a expressão, encontramos a soma total da série telescópica.

Agora que você sabe como resolver uma série telescópica, vamos praticar com alguns exercícios resolvidos:

Exercício 1: Encontre a soma total da série (S = 1 + frac{1}{2} + frac{1}{4} + frac{1}{8} + cdots + frac{1}{2^n}).

Solução: Neste caso, a expressão geral da série é (S = sum_{n=0}^{N} frac{1}{2^n}). Simplificando a expressão, obtemos (S = 2 – frac{1}{2^n}). Substituindo (n) pelo número desejado, encontramos a soma total da série.

Com esses passos simples, você pode resolver facilmente uma série telescópica e encontrar a soma total em apenas alguns passos. Pratique com diferentes exemplos para aprimorar suas habilidades em somatórios telescópicos.

Somatório telescópico: como é resolvido e exercícios resolvidos

O somatório telescópico é um ramo de operações com séries numéricas. Ele aborda as somas de elementos de um valor inicial a “n” de expressões cujo argumento obedece a qualquer um dos seguintes padrões:

(F _x – F _{x + 1} ); (F _{x + 1} – F _x )

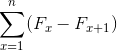
Como também:

Eles representam uma soma de elementos que, quando desenvolvidos, estão sujeitos a cancelamentos de termos opostos. Tornando possível definir a seguinte igualdade para somas telescópicas:

Seu nome deriva do relacionamento com a aparência de um telescópio clássico, que poderia ser dobrado e implantado, mudando significativamente sua dimensão. Da mesma forma, os somatórios telescópicos, de natureza infinita, podem ser resumidos na expressão simplificada:

F ₁ – F _{n + 1}

Demonstração

Ao desenvolver a soma dos termos, a eliminação de fatores é bastante óbvia. Onde, para cada um dos casos, elementos opostos aparecerão na próxima iteração.

O primeiro caso, (F _x – F _{x + 1} ), será tomado como exemplo , pois o processo funciona de maneira homóloga para (F _{x + 1 –} F _x ).

Desenvolvendo os 3 primeiros valores {1, 2, 3}, observa-se a tendência de simplificação

X ₁ (F ₁ – F _{1 + 1} ) = F ₁ – F ₂

X ₂ (F ₂ – F _{2 + 1} ) = F ₂ – F ₃

X ₃ (F ₃ – F _{3 + 1} ) = F ₃ – F ₄

Onde, ao expressar a soma dos elementos descritos:

X ₁ + X ₂ + X ₃ = F ₁ – F ₂ + F ₂ – F ₃ + F ₃ – F ₄

Note-se que os termos F ₂ e F ₃ são descritos juntamente com seus opostos, o que torna sua simplificação inevitável. Da mesma forma que é notado que os termos de F ₁ e F ₄ são mantidas.

Se a soma foi feita de x = 1 a x = 3, significa que o elemento F ₄ corresponde ao termo genérico F _{n + 1.}

Demonstrando assim a igualdade:

Como é resolvido?

O objetivo das somas telescópicas é facilitar o trabalho, de modo que não seja necessário desenvolver uma quantidade infinita de termos ou simplificar por muito tempo uma cadeia de adendos.

Para sua resolução, somente será necessário avaliar os termos F ₁ e F _{n + 1} . Essas substituições simples compõem o resultado final da soma.

A totalidade dos termos não será expressa, tornando-se necessária apenas para a demonstração do resultado, mas não para o processo normal de cálculo.

O importante é notar a convergência das séries numéricas. Às vezes, o argumento da soma não será expresso telescopicamente. Nesses casos, a implementação de métodos alternativos de fatoração é muito comum.

O método de fatoração característico em somas telescópicas é o de frações simples. Isso ocorre quando uma fração original é dividida em uma soma de várias frações, onde o padrão telescópico (F _x – F _{x + 1} ) ou (F _{x + 1} – F _x ) pode ser observado .

Decomposição em frações simples

Para verificar a convergência das séries numéricas, é muito comum transformar expressões racionais com o método de frações simples. O objetivo é modelar o argumento para dar a forma de um somatório telescópico.

Por exemplo, a seguinte igualdade representa uma decomposição em frações simples:

Ao desenvolver a série numérica e aplicar as propriedades correspondentes, a expressão assume a seguinte forma:

Onde você pode ver a forma telescópica (F _x – F _{x + 1} ).

O procedimento é bastante intuitivo e consiste em encontrar os valores do numerador que, sem quebrar a igualdade, permitem separar os produtos que estão no denominador. As equações que surgem na determinação desses valores são apresentadas de acordo com comparações entre os dois lados da igualdade.

Este procedimento é observado passo a passo no desenvolvimento do exercício 2.

História

É bastante incerto poder definir o momento histórico em que os somatórios telescópicos foram apresentados. No entanto, sua implementação começa a ser vista no século XVII, nos estudos de séries numéricas realizadas por Leibniz e Huygens.

Ambos os matemáticos, ao explorar a soma de números triangulares, começam a notar tendências na convergência de certas séries de elementos sucessivos. Mas ainda mais interessante é o início da modelagem dessas expressões, em elementos que não necessariamente acontecem.

De fato, a expressão usada anteriormente para se referir a frações simples:

Foi apresentado por Huygens e imediatamente chamou a atenção de Leibniz. Quem, com o tempo, pôde observar a convergência para o valor 2. Sem saber, ele implementou o formato de soma telescópica.

Exercícios

Exercício 1

Defina para qual termo a seguinte soma converge:

Ao desenvolver manualmente a soma, o seguinte padrão é observado:

(2 ³ – 2 ⁴ ) + (2 ⁴ – 2 ⁵ ) + (2 ⁵ – 2 ⁶ ). . . . (2 ¹⁰ – 2 ¹¹ )

Onde os fatores de 2 ⁴ a 2 ¹⁰ têm partes positivas e negativas, evidenciando seu cancelamento. Os únicos fatores que não serão simplificados serão o primeiro “2 ³ ” e o último “2 ¹¹ “.

Dessa maneira, ao implementar os critérios de soma telescópica, você obtém:

Exercício 2

Transforme o argumento em uma soma do tipo telescópico e defina a convergência da série:

Conforme indicado na declaração, a primeira coisa será realizar a decomposição em frações simples, a fim de repensar o argumento e expressá-lo telescopicamente.

Você deve encontrar 2 frações cujos denominadores são respectivamente “n” e “n + 1”, onde o método usado abaixo deve atingir os valores do numerador que atendem à igualdade.

São definidos os valores de A e B. Primeiro, é feita a soma das frações.

Em seguida, os denominadores são simplificados e uma equação linear é estabelecida.

Na próxima etapa, a expressão à direita é operada, até que um padrão comparável ao “3” à esquerda seja alcançado.

Para definir as equações a serem usadas, os resultados de ambos os lados da igualdade devem ser comparados. Ou seja, nenhum valor da variável n é observado no lado esquerdo, então A + B terá que ser igual a zero.

A + B = 0; A = -B

Por outro lado, o valor constante A terá que ser igual ao valor constante 3.

A = 3

Portanto.

A = 3 e B = -3

Depois que os valores do numerador tiverem sido definidos para frações simples, o somatório será reajustado.

Onde a forma de soma telescópica genérica já foi alcançada. A série telescópica é desenvolvida.

Onde, ao dividir por um número muito grande, o resultado estará cada vez mais próximo de zero, observando a convergência da série com o valor 3.

Esse tipo de série não poderia ser resolvido de outra forma, devido à quantidade infinita de iterações que definem o problema. No entanto, esse método, juntamente com muitos outros, enquadra o ramo de estudo das séries numéricas, cujo objetivo é determinar os valores de convergência ou definir a divergência dessas séries.

Referências

1. Lições de cálculo infinitesimal. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. EDITUM, 1994.
2. Cálculo Integral: Sucessões e Séries de Funções. Antonio Rivera Figueroa. Patria Editorial Group, 21 de outubro. 2014
3. Um Curso de Cálculo e Análise Real. Sudhir R. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 de junho 2006
4. Série infinita Tomlinson Fort. The Clarendon Press, 1930.
5. Elementos da teoria dos processos infinitos. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorporado, 1923.