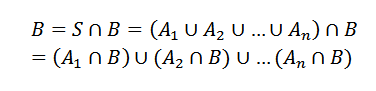O Teorema de Bayes é um conceito fundamental da teoria da probabilidade que descreve como as probabilidades de eventos são atualizadas à medida que novas informações são obtidas. Neste artigo, vamos explicar o Teorema de Bayes de forma clara e concisa, discutir suas aplicações práticas em diversos campos, como estatística, machine learning e medicina, e apresentar alguns exercícios para ajudar na compreensão e aplicação desse importante conceito matemático.
Aplicando o teorema de Bayes: passo a passo para uma análise probabilística eficaz.
Aplicando o teorema de Bayes, podemos realizar uma análise probabilística eficaz em diversos contextos. Este teorema, formulado pelo matemático Thomas Bayes, permite atualizar a probabilidade de um evento com base em novas informações.
Para utilizar o teorema de Bayes, primeiro precisamos identificar as probabilidades iniciais de cada evento. Em seguida, devemos considerar as novas informações disponíveis e calcular como essas informações afetam as probabilidades iniciais.
Um passo importante no processo é determinar a probabilidade condicional, que representa a probabilidade de um evento ocorrer dado que outro evento já ocorreu. Essa informação é essencial para aplicar o teorema de Bayes corretamente.
Com as probabilidades iniciais e as informações adicionais em mãos, podemos então aplicar o teorema de Bayes para atualizar as probabilidades e obter uma análise mais precisa. Esse método é amplamente utilizado em áreas como a medicina, a engenharia, a economia e a inteligência artificial.
Em resumo, o teorema de Bayes é uma ferramenta poderosa para realizar análises probabilísticas de forma eficaz. Ao seguir os passos corretos e considerar as informações relevantes, podemos obter resultados mais precisos e tomar decisões mais embasadas em diversos contextos.
Entendendo a essência da regra de Bayes: princípio fundamental da probabilidade condicional.
Entendendo a essência da regra de Bayes: princípio fundamental da probabilidade condicional.
O Teorema de Bayes é uma ferramenta fundamental na teoria da probabilidade, que permite calcular a probabilidade de um evento baseado em informações prévias. Ele é frequentemente utilizado em estatística, machine learning e outras áreas onde a incerteza é um fator importante.
A essência da regra de Bayes reside na ideia de probabilidade condicional, que é a probabilidade de um evento A ocorrer dado que um evento B já ocorreu. Em termos simples, a regra de Bayes nos permite atualizar nossas crenças sobre a probabilidade de um evento à medida que obtemos novas informações.
Para aplicar o Teorema de Bayes, é necessário levar em consideração a probabilidade dos eventos anteriores, a probabilidade dos eventos condicionais e a probabilidade dos eventos conjuntos. Ao combinar essas informações, podemos obter uma estimativa mais precisa da probabilidade de um evento.
As aplicações do Teorema de Bayes são vastas e variadas. Ele é utilizado em áreas como medicina, economia, engenharia, entre outras. Por exemplo, na medicina, o Teorema de Bayes pode ser usado para diagnosticar doenças com base em sintomas apresentados pelo paciente.
Para praticar a aplicação do Teorema de Bayes, é útil resolver exercícios que envolvam cálculos de probabilidade condicional. A prática constante ajuda a aprimorar a compreensão e a habilidade de aplicar a regra de Bayes em diferentes situações.
Em resumo, entender a essência da regra de Bayes é essencial para quem trabalha com probabilidades e estatísticas. Ao dominar esse princípio fundamental da probabilidade condicional, é possível tomar decisões mais embasadas e precisas em diversas áreas do conhecimento.
Descubra o método para calcular a probabilidade total em diferentes cenários de eventos.
O Teorema de Bayes é um conceito fundamental na teoria da probabilidade que nos permite calcular a probabilidade de um evento com base em informações prévias. Ele é especialmente útil em situações onde temos múltiplos eventos e queremos determinar a probabilidade de um deles ocorrer.
O Teorema de Bayes é baseado na ideia de probabilidade condicional, que é a probabilidade de um evento A ocorrer dado que outro evento B já ocorreu. A fórmula do Teorema de Bayes é expressa da seguinte forma:
P(A|B) = P(B|A) * P(A) / P(B)
Onde:
P(A|B) é a probabilidade de A dado B.
P(B|A) é a probabilidade de B dado A.
P(A) é a probabilidade de A ocorrer.
P(B) é a probabilidade de B ocorrer.
O Teorema de Bayes tem diversas aplicações em áreas como medicina, economia, ciência de dados e muitas outras. Ele é utilizado para fazer previsões, diagnósticos e tomar decisões com base em informações probabilísticas.
Para entender melhor como o Teorema de Bayes funciona, vamos resolver um exercício simples:
Suponha que em uma cidade, 60% dos acidentes de trânsito são causados por motoristas distraídos e 40% são causados por problemas mecânicos nos veículos. Sabendo que 50% dos motoristas são distraídos e 20% dos veículos apresentam problemas mecânicos, qual a probabilidade de um acidente ter sido causado por um motorista distraído?
Utilizando o Teorema de Bayes, podemos calcular a probabilidade da seguinte forma:
P(Motorista distraído|Acidente) = P(Acidente|Motorista distraído) * P(Motorista distraído) / P(Acidente)
Substituindo os valores na fórmula, temos:
P(Motorista distraído|Acidente) = 0.60 * 0.50 / (0.60 * 0.50 + 0.40 * 0.20) = 0.75
Portanto, a probabilidade de um acidente ter sido causado por um motorista distraído é de 75%.
Exemplos de probabilidade condicional: o que é e como calcular corretamente.
Probabilidade condicional é a probabilidade de um evento ocorrer, dado que outro evento já ocorreu. Para calcular corretamente a probabilidade condicional, usamos a fórmula:
P(A|B) = P(A e B) / P(B)
Onde P(A|B) é a probabilidade de A ocorrer dado que B já ocorreu, P(A e B) é a probabilidade de ambos A e B ocorrerem juntos, e P(B) é a probabilidade de B ocorrer.
Um exemplo de probabilidade condicional é o seguinte: qual a probabilidade de chover dado que as nuvens estão carregadas? Neste caso, a probabilidade de chover (A) dado que as nuvens estão carregadas (B) seria calculada usando a fórmula acima.
Teorema de Bayes: explicação, aplicações, exercícios.
O Teorema de Bayes é uma fórmula que nos permite atualizar nossas crenças sobre a probabilidade de um evento, dado novas evidências. Ele é muito útil em áreas como estatística, inteligência artificial e medicina.
A fórmula do Teorema de Bayes é:
P(A|B) = P(B|A) * P(A) / P(B)
Onde P(A|B) é a probabilidade de A dado B, P(B|A) é a probabilidade de B dado A, P(A) é a probabilidade de A e P(B) é a probabilidade de B.
Um exemplo de aplicação do Teorema de Bayes é na área médica, onde ele pode ser usado para diagnosticar doenças com base em sintomas apresentados pelos pacientes.
Um exercício comum envolvendo o Teorema de Bayes seria calcular a probabilidade de uma pessoa ter uma determinada doença, dado que o resultado de um teste específico foi positivo. Este cálculo pode ser feito usando a fórmula acima.
Teorema de Bayes: explicação, aplicações, exercícios
O Teorema de Bayes é um procedimento que nos permite expressar a probabilidade condicional de um evento aleatório A dado B, em termos da distribuição de probabilidade do evento B dado A e da distribuição de probabilidade de apenas A.
Esse teorema é muito útil, porque, graças a ele, podemos relacionar a probabilidade de um evento A ocorrer sabendo que B ocorreu, com a probabilidade de que o contrário aconteça, ou seja, que B ocorra A.
O teorema de Bayes foi uma proposição de prata do Rev. Thomas Bayes, um teólogo inglês do século XVIII que também era matemático. Ele foi autor de vários trabalhos em teologia, mas atualmente é conhecido por alguns tratados matemáticos, entre os quais o referido teorema de Bayes se destaca como o principal resultado.
Bayes lidou com esse teorema em um trabalho intitulado “Um ensaio para resolver um problema na doutrina das possibilidades”, publicado em 1763, e sobre o qual grandes estudos com aplicações em diversas áreas do conhecimento.
Explicação
Primeiro, para uma melhor compreensão desse teorema, são necessárias algumas noções básicas da teoria da probabilidade, especialmente o teorema da multiplicação para probabilidade condicional, que afirma que
Para eventos arbitrários E e A de um espaço de amostra S.
E a definição de partições, que nos diz que se tivermos eventos A 1 , A 2 , …, A n de um espaço de amostra S, eles formarão uma partição de S, se A i for mutuamente exclusiva e sua união for S.
Tendo isso, deixe B ser outro evento. Então podemos ver B como
Onde A e cruzados com B são eventos mutuamente exclusivos.
E, consequentemente,
Em seguida, aplicando o teorema da multiplicação
Por outro lado, a probabilidade condicional de Ai dada B é definida por
Substituindo corretamente, temos que para qualquer i
Aplicações do Teorema de Bayes
Graças a esse resultado, diversos grupos de pesquisa e empresas conseguiram melhorar sistemas baseados no conhecimento.
Por exemplo, no estudo de doenças, o teorema de Bayes pode ajudar a discernir a probabilidade de uma doença ser encontrada em um grupo de pessoas com uma determinada característica, tomando como dados as taxas gerais da doença e a prevalência dessas características em pessoas saudáveis e doentes.
Por outro lado, no mundo das altas tecnologias, influenciou grandes empresas que desenvolveram, graças a esse resultado, software “Knowledge Based”.
Como exemplo diário, temos o assistente do Microsoft Office. O teorema de Bayes ajuda o software a avaliar os problemas apresentados pelo usuário e determinar quais conselhos fornecer e, assim, poder oferecer um serviço melhor de acordo com os hábitos do usuário.
Deve-se notar que essa fórmula foi ignorada até tempos recentes, principalmente devido ao fato de que quando esse resultado foi desenvolvido há 200 anos, havia pouco uso prático para elas. No entanto, em nossos dias, graças aos grandes avanços tecnológicos, os cientistas conseguiram maneiras de colocar esse resultado em prática.
Exercícios resolvidos
Exercício 1
Uma empresa de telefonia celular possui duas máquinas A e B. 54% dos celulares produzidos são fabricados pela máquina A e os demais pela máquina B. Nem todos os celulares produzidos estão em boas condições.
A proporção de telefones celulares defeituosos fabricados por A é de 0,2 e por B é de 0,5. Qual é a probabilidade de um telefone celular daquela fábrica estar com defeito? Qual é a probabilidade de que, sabendo que um telefone celular esteja com defeito, ele venha da máquina A?
Solução
Aqui, você tem um experimento feito em duas partes; Na primeira parte, os eventos ocorrem:
A: telefone celular feito pela máquina A.
B: telefone celular fabricado pela máquina B.
Como a máquina A produz 54% dos telefones celulares e o restante é produzido pela máquina B, a máquina B possui 46% dos telefones celulares. As probabilidades desses eventos são dadas, a saber:
P (A) = 0,54.
P (B) = 0,46.
Os eventos da segunda parte do experimento são:
D: telefone celular com defeito.
E: telefone celular não está com defeito.
Conforme declarado na declaração, as probabilidades desses eventos dependem do resultado obtido na primeira parte:
P (D | A) = 0,2.
P (D | B) = 0,5.
Usando esses valores, você também pode determinar as probabilidades dos complementos desses eventos, ou seja:
P (E | A) = 1 – P (D | A)
= 1 – 0,2
= 0,8
e
p (E | B) = 1 – P (D | B)
= 1 – 0,5
= 0,5
Agora, o evento D pode ser escrito da seguinte maneira:
Usando o teorema da multiplicação para obter resultados de probabilidade condicional:
Com o qual a primeira pergunta é respondida.
Agora, apenas precisamos calcular P (A | D), ao qual o Teorema de Bayes se aplica:
Graças ao Teorema de Bayes, pode-se afirmar que a probabilidade de um telefone celular ter sido fabricado pela máquina A, sabendo que o telefone está com defeito, é 0,319.
Exercício 2
Três caixas contêm bolas preto e brancas. A composição de cada um deles é a seguinte: U1 = {3B, 1N}, U2 = {2B, 2N}, U3 = {1B, 3N}.
Uma das caixas é escolhida aleatoriamente e uma bola aleatória é extraída dela, que acaba sendo branca. Qual caixa é mais provável de ter sido escolhida?
Solução
Através de U1, U2 e U3, também representaremos a caixa escolhida.
Esses eventos constituem uma partição de S e verifica-se que P (U1) = P (U2) = P (U3) = 1/3, pois a escolha da caixa é aleatória.
Se B = {a bola extraída for branca}, teremos P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4.
O que queremos obter é a probabilidade de a bola ter sido retirada da caixa Ui sabendo que a bola era branca, ou seja, P (Ui | B), e ver qual dos três valores foi o mais alto para saber qual caixa tem mais probabilidade de extrair a bola branca.
Aplicando o teorema de Bayes à primeira das caixas:
E para os outros dois:
P (U2 | B) = 2/6 e P (U3 | B) = 1/6.
Então, a primeira das caixas é a que mais provavelmente foi escolhida para a extração da bola branca.
Referências
- Kai Lai Chung Teoria Elementar da Probabilidade com Processos Estocásticos. Springer-Verlag Nova Iorque Inc
- Kenneth.H. Rosen – Matemática Discreta e suas Aplicações. SAMCGRAW-HILL / INTERAMERICANO DE ESPANHA.
- Paul L. Meyer Probabilidade e aplicações estatísticas. SA ALHAMBRA MEXICANA.
- Seymour Lipschutz Ph.D. 2000 Resolvidos problemas de matemática discreta. McGRAW-HILL
- Seymour Lipschutz Ph.D. Problemas de teoria e probabilidade. McGRAW-HILL