A proporcionalidade composta é um conceito matemático que envolve a relação entre grandezas diretamente proporcionais ou inversamente proporcionais. Neste contexto, a regra composta três é uma ferramenta utilizada para resolver problemas que envolvem mais de duas grandezas proporcionais.
Neste artigo, vamos explicar o conceito de proporcionalidade composta, apresentar a regra composta três e fornecer alguns exemplos de exercícios resolvidos para ajudar na compreensão e fixação do conteúdo. A proporcionalidade composta é um tema importante na matemática e é fundamental para resolver problemas do dia a dia que envolvem a relação entre diferentes grandezas. Vamos explorar esse conceito e suas aplicações através de exercícios práticos.
Explicando de forma simples a regra de 3 composta em situações práticas do dia a dia.
Para entender a regra de 3 composta, é importante primeiro lembrar da regra de 3 simples. Na regra de 3 simples, comparamos duas grandezas diretamente proporcionais ou inversamente proporcionais. Já na regra de 3 composta, vamos lidar com mais de duas grandezas de forma proporcional.
Vamos exemplificar para facilitar o entendimento. Imagine que você precise calcular quanto tempo levará para pintar uma parede com três amigos, sabendo que cada um deles leva um tempo diferente para realizar a tarefa. Digamos que o amigo A leva 4 horas, o amigo B leva 6 horas e o amigo C leva 8 horas para pintar a mesma parede sozinhos.
A regra de 3 composta nos ajuda a descobrir quanto tempo levarão juntos para pintar a parede. Primeiramente, calculamos a parte inversa do tempo de cada amigo: 1/4, 1/6 e 1/8. Em seguida, somamos esses valores: 1/4 + 1/6 + 1/8 = 7/24. Por fim, dividimos 1 pela soma obtida, que resulta em aproximadamente 3,42 horas.
Portanto, com a regra de 3 composta, conseguimos determinar o tempo necessário para realizar uma atividade envolvendo mais de duas grandezas de forma proporcional. Praticar exercícios e aplicar essa regra em situações do dia a dia ajuda a fixar o conhecimento e aperfeiçoar o raciocínio matemático.
Entenda a aplicação da regra de 3 com exemplos práticos e simples.
A regra de 3 é um método matemático utilizado para resolver problemas de proporcionalidade entre grandezas. Ela é muito útil em situações do dia a dia, como cálculos de porcentagens, regras de divisão de custos, entre outros.
Para aplicar a regra de 3, é necessário estabelecer uma relação de proporcionalidade entre duas grandezas. A partir disso, é possível encontrar o valor de uma terceira grandeza desconhecida.
Um exemplo simples de aplicação da regra de 3 é o seguinte: se 2 litros de suco custam R$ 4, qual o valor de 5 litros desse mesmo suco? Para resolver esse problema, basta estabelecer a proporção entre litros e custo, e então fazer a regra de 3 para encontrar o valor correto.
Agora, vamos falar sobre a proporcionalidade composta. Nesse caso, a regra de 3 é aplicada quando há mais de duas grandezas envolvidas. Para resolver problemas de proporcionalidade composta, é necessário estabelecer uma relação entre todas as grandezas e então fazer os cálculos necessários para encontrar o valor desconhecido.
Um exemplo de proporcionalidade composta seria o seguinte: se 3 operários levam 4 dias para construir uma casa, quantos dias serão necessários para 5 operários construírem a mesma casa? Nesse caso, é preciso estabelecer a relação entre o número de operários e o tempo de construção, e então aplicar a regra de 3 composta para encontrar a resposta.
A prática de exercícios é fundamental para compreender e dominar a aplicação da regra de 3 e da proporcionalidade composta. Por isso, é importante resolver diversos problemas e situações do cotidiano que envolvam esses conceitos, a fim de aprimorar o raciocínio matemático e a capacidade de resolução de problemas.
Resolvendo problemas de proporção através da regra de três de maneira simples.
Resolver problemas de proporção através da regra de três é uma forma simples e eficaz de encontrar a resposta correta. A proporcionalidade composta é uma extensão desse conceito, que envolve mais de duas grandezas proporcionais. Para resolver problemas de proporcionalidade composta, basta seguir a mesma lógica da regra de três, considerando todas as grandezas envolvidas.
A regra de três simples consiste em estabelecer uma proporção entre duas grandezas, de forma que se uma delas aumenta, a outra também aumenta na mesma proporção. Já a regra de três composta envolve mais de duas grandezas, mas o princípio é o mesmo: manter a proporção entre elas.
Para resolver um problema de proporcionalidade composta, basta identificar as grandezas envolvidas, estabelecer a proporção correta entre elas e fazer os cálculos necessários. É importante manter a lógica de que se uma grandeza aumenta, as outras também devem aumentar na mesma proporção, e vice-versa.
Para fixar o conceito, vamos resolver um exercício simples de proporcionalidade composta: Se 2 litros de suco custam R$5,00, quanto custará 5 litros desse mesmo suco? Utilizando a regra de três composta, temos: 2 litros – R$5,00; 5 litros – x. Assim, podemos encontrar o valor de x através da proporção correta entre as grandezas.
Portanto, resolver problemas de proporcionalidade composta através da regra de três é uma maneira simples e eficaz de encontrar a resposta correta. Com um pouco de prática, é possível dominar esse conceito e aplicá-lo em diferentes situações do dia a dia.
Identificando se a regra de 3 é composta e direta, inversa ou simples.
Na matemática, quando falamos em proporção, estamos nos referindo à relação entre grandezas, de modo que quando uma aumenta, a outra também aumenta (proporção direta) ou quando uma aumenta, a outra diminui (proporção inversa). A regra de 3 é um método utilizado para resolver problemas de proporção de forma simples e eficiente.
Existem diferentes tipos de regra de 3, sendo a mais comum a regra de 3 simples, que é utilizada quando temos apenas duas grandezas diretamente proporcionais. Já a regra de 3 composta é aplicada quando temos mais de duas grandezas e elas podem ser diretamente ou inversamente proporcionais entre si.
Para identificar se a regra de 3 é composta e direta, inversa ou simples, basta analisar as grandezas envolvidas no problema e verificar se há mais de duas grandezas e se a relação entre elas é direta ou inversa. Caso haja mais de duas grandezas e elas se relacionem de forma direta ou inversa, estaremos lidando com a regra de 3 composta.
Proporcionalidade composta: explicação, regra composta três, exercícios
A proporcionalidade compósito ou múltipla é a proporção de mais de duas grandezas, que pode ser observada directamente e proporcionalidade inversa entre os dados e o desconhecido. Esta é uma versão mais avançada da proporcionalidade simples, embora as técnicas usadas nos dois procedimentos sejam semelhantes.
Por exemplo, se forem necessárias 7 pessoas para descarregar 10 toneladas de mercadorias em 3 horas, a proporcionalidade composta pode ser usada para calcular quantas pessoas serão necessárias para descarregar 15 toneladas em 4 horas.

Para responder a essa pergunta, é conveniente fazer uma tabela de valores para estudar e relacionar magnitudes e incógnitas.

Passamos a analisar os tipos de relações entre cada magnitude e o presente desconhecido, que neste caso corresponde ao número de pessoas que trabalharão.
À medida que o peso da mercadoria aumenta, o número de pessoas necessárias para fazer o download também aumenta. Por isso, a relação entre peso e trabalhadores é direta.
Por outro lado, à medida que o número de trabalhadores aumenta, as horas de trabalho diminuem. Por esse motivo, a relação entre pessoas e horas de trabalho é do tipo inverso.
Como calcular proporções compostas
Para resolver exemplos como o anterior, o método da regra dos três compostos é usado principalmente. Isso é para estabelecer os tipos de relacionamentos entre quantidades e incógnitas e, em seguida, representar um produto entre frações.
Com relação ao exemplo inicial, as frações correspondentes à tabela de valores estão organizadas da seguinte forma:
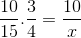
Mas antes de resolver e limpar o desconhecido, as frações correspondentes à relação inversa devem ser revertidas. Que para este caso corresponde à variável de tempo. Dessa maneira, a operação a ser resolvida será:

Cuja única diferença é a inversão da fração correspondente à variável de tempo 4/3. Prosseguimos para operar e limpar o valor de x.

Assim, são necessárias mais de onze pessoas para poder descarregar 15 toneladas de mercadorias em 4 horas ou menos.
Explicação
Proporcionalidade é a relação constante entre magnitudes sujeitas a alterações, que será simétrica para cada uma das magnitudes envolvidas. Existem relações proporcionais direta e inversamente definidas, definindo assim os parâmetros de proporcionalidade simples ou composta.
Regra direta de três
Consiste em uma relação de razão entre variáveis, que tem o mesmo comportamento quando modificadas. É muito frequente no cálculo de porcentagens referentes a magnitudes diferentes de cem, onde é apreciada sua estrutura fundamental.
Como exemplo, pode-se calcular 15% de 63. À primeira vista, esse percentual não pode ser visto facilmente. Mas, ao implementar a regra dos três, é possível estabelecer o seguinte relacionamento: se 100% for 63, então 15%, quanto será?
100% ———- 63
15% ———– X
E a operação correspondente é:
(15%. 63) / 100% = 9,45
Onde os sinais de porcentagem são simplificados e a figura 9.45 é obtida, o que representa 15% de 63.
Regra inversa de três
Como o nome indica, neste caso, a relação entre as variáveis é contrária. A relação inversa deve ser estabelecida antes de prosseguir com o cálculo. Seu procedimento é homólogo ao da regra direta de três, exceto pelo investimento na fração a ser calculada.
Por exemplo, três pintores precisam de 5 horas para terminar uma parede. Em quantas horas 4 pintores terminariam?
Nesse caso, a relação é inversa, pois à medida que o número de pintores aumenta, o tempo de trabalho deve diminuir. O relacionamento é estabelecido;
3 pintores – 5 horas
4 pintores – X horas
Quando o relacionamento é inverso, a ordem da operação é revertida. Este é o caminho certo;
(3 pintores). (5 horas) / 4 pintores = 3,75 horas
O termo pintores é simplificado e o resultado é 3,75 horas.
Condição
Para estar na presença de uma proporcionalidade composta ou múltipla, é necessário encontrar os dois tipos de relacionamento entre as magnitudes e as variáveis.
– Direto: a variável tem o mesmo comportamento que o desconhecido. Ou seja, quando um aumenta ou diminui, o outro é alterado igualmente.
– Reverso: a variável tem um comportamento antônimo para o desconhecido. Você deve inverter a fração que define essa variável na tabela de valores, para representar a relação inversamente proporcional entre variável e desconhecido.
Verificação de resultados
É muito comum confundir a ordem das magnitudes ao trabalhar com proporções compostas, ao contrário do que acontece nos cálculos de proporção usuais, cuja natureza é principalmente direta e solucionável pela simples regra de três.
Portanto, é importante examinar a ordem lógica dos resultados, verificando a consistência dos números dados pela regra dos três compostos.
No exemplo inicial, cometer esse erro significaria obter 20 como resultado. Ou seja, 20 pessoas para descarregar 15 toneladas de mercadorias em 4 horas.
À primeira vista, não parece um resultado louco, mas é curioso um aumento de quase 200% na equipe (de 7 para 20 pessoas) quando o aumento da mercadoria é de 50%, e mesmo com uma maior margem de tempo para obter o trabalho.
Dessa maneira, a verificação lógica dos resultados representa uma etapa importante na implementação da regra de três compostos.
Liquidação
Embora de natureza mais básica em relação ao treinamento matemático, a liberação representa um passo importante em casos de proporcionalidade. Uma liberação incorreta é suficiente para invalidar qualquer resultado obtido em uma regra simples ou composta de três.
História
A regra dos três tornou-se conhecida no Ocidente através dos árabes, com publicações de vários autores. Entre eles, Al-Jwarizmi e Al-Biruni.
Al-Biruni, graças ao seu conhecimento multicultural, teve acesso a vastas informações sobre essa prática em suas viagens à Índia, sendo responsável pela documentação mais extensa sobre a regra de três.
Ele afirma em sua investigação que a Índia foi o primeiro lugar em que o uso da regra dos três se tornou comum. O escritor garante que foi efetuado com fluidez em suas versões direta, reversa e até composta.
A data exata em que a regra dos três se tornou parte do conhecimento matemático da Índia ainda é desconhecida. No entanto, o documento mais antigo endereçado a essa prática, o manuscrito de Bakhshali, foi descoberto em 1881. Atualmente, está em Oxford.
Muitos historiadores da matemática afirmam que este manuscrito data do início da era atual.
Exercícios resolvidos
Exercício 1
Uma companhia aérea deve transportar 1535 pessoas. Sabe-se que, com três aviões, levaria 12 dias para levar o último passageiro ao seu destino. Mais 450 pessoas chegaram à companhia aérea e 2 aviões foram solicitados a reparar para ajudar nessa tarefa. Quantos dias leva para a companhia aérea transferir o último passageiro para o seu destino?
A relação entre o número de pessoas e os dias de trabalho é direta, porque quanto mais pessoas, mais dias serão necessários para realizar esse trabalho.
Por outro lado, a relação entre aviões e dias é inversamente proporcional. À medida que o número de aeronaves aumenta, os dias necessários para transferir todos os passageiros diminuem.
A tabela de valores referente a este caso é feita.

Conforme detalhado no exemplo inicial, o numerador e o denominador devem ser revertidos na fração correspondente à variável inversa em relação ao desconhecido. A operação é a seguinte:

X = 71460/7675 = 9,31 dias
Para transportar 1985 pessoas usando 5 aviões, são necessários mais de 9 dias.
Exercício 2
Uma safra de milho de 25 toneladas é levada para os caminhões de carga. Sabe-se que o ano anterior levou 8 horas com uma folha de pagamento de 150 trabalhadores. Se neste ano a folha de pagamento aumentar em 35%, quanto tempo levará para encher os caminhões de carga com uma safra de 40 toneladas?
Antes de representar a tabela de valores, o número de trabalhadores para este ano deve ser definido. Isso aumentou em 35% do número inicial de 150 trabalhadores. Para isso, uma regra direta de três é usada.
100% – 150
35% ———– X
X = (35, 100) / 100 = 52,5. Este é o número de trabalhadores adicionais em relação ao ano anterior, obtendo um número total de trabalhadores de 203, depois de arredondar o valor obtido.
A tabela de dados correspondente é definida

Para este caso, o peso representa uma variável de relação direta com o tempo desconhecido. Por outro lado, a variável workers lida com uma relação inversa com o tempo. Quanto maior o número de trabalhadores, o dia será mais curto.
Levando em consideração essas considerações e investindo a fração correspondente à variável trabalhadores, procedemos ao cálculo.
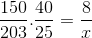
X = 40600/6000 = 6,76 horas
O dia levará um pouco menos de 7 horas.
Exercícios propostos
– Defina 73% de 2875.
– Calcule o número de horas que Teresa dorme, se souber que apenas 7% do dia total dorme. Defina quantas horas você dorme por semana.
– Um jornal publica 2000 cópias a cada 5 horas, usando apenas 2 máquinas de impressão. Quantas cópias você produzirá em 1 hora, se você usar 7 máquinas? Quanto tempo ele produzirá 10.000 cópias usando 4 máquinas?
Referências
- Enciclopédia Alvarez-iniciação. A. Álvarez, Antonio Álvarez Pérez. EDAF, 2001.
- Manual completo do ensino fundamental e ensino fundamental: para o uso de aspirantes a professores e especialmente estudantes das Escolas Normais da Província, volume 1. Joaquín Avendaño. Impressão de D. Dionisio Hidalgo, 1844.
- Aproximação racional de funções reais. PP Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 de março 2011
- Aritmética elementar para o ensino em escolas e faculdades da América Central. Darío González. Dica Arenales, 1926.
- O Estudo da Matemática: Sobre o estudo e as dificuldades da matemática. Augustus De Morgan. Baldwin e Cradock, 1830.