O tiro parabólico oblíquo é um tipo de movimento de projétil que ocorre quando um objeto é lançado com uma velocidade inicial em um ângulo em relação à horizontal. Nesse tipo de movimento, o objeto descreve uma trajetória em forma de parábola devido à ação da gravidade sobre ele.
Para descrever o tiro parabólico oblíquo, são utilizadas diversas fórmulas e equações que levam em consideração a velocidade inicial, o ângulo de lançamento, a aceleração da gravidade e a altura inicial do objeto. Essas equações permitem calcular a altura máxima atingida pelo objeto, o alcance horizontal, o tempo de voo e a velocidade em qualquer ponto da trajetória.
Alguns exemplos de tiro parabólico oblíquo incluem o lançamento de uma bola de basquete, a trajetória de um foguete ou o arremesso de um objeto em um jogo esportivo. Este tipo de movimento é comum em diversas situações do dia a dia e é fundamental para compreender a física por trás do movimento de projéteis.
Fórmulas para cálculo do lançamento oblíquo: o que você precisa saber.
Quando se trata de calcular o lançamento oblíquo, é importante ter em mente algumas fórmulas e equações que facilitarão o processo. Para começar, é fundamental lembrar que o tiro parabólico oblíquo é um movimento que ocorre quando um objeto é lançado com uma certa velocidade inicial e um ângulo em relação à horizontal.
As fórmulas principais para calcular o lançamento oblíquo são as seguintes:
Altura máxima: h = (v₀² * sen²θ) / 2g
Alcance máximo: R = (v₀² * sen2θ) / g
Tempo de voo: t = (2 * v₀ * senθ) / g
É importante lembrar que na fórmula da altura máxima, h representa a altura máxima atingida pelo objeto, v₀ é a velocidade inicial, θ é o ângulo de lançamento e g é a aceleração da gravidade.
Por outro lado, na fórmula do alcance máximo, R representa a distância percorrida pelo objeto, v₀ é novamente a velocidade inicial, θ é o ângulo de lançamento e g é a aceleração da gravidade.
Para calcular o tempo de voo, é necessário levar em consideração a velocidade inicial v₀, o ângulo de lançamento θ e a aceleração da gravidade g.
Características do movimento oblíquo: o que você precisa saber sobre essa trajetória curva.
O movimento oblíquo é caracterizado por uma trajetória curva que combina movimento horizontal e vertical. Essa trajetória é resultado da combinação da velocidade inicial do objeto lançado e da aceleração da gravidade. Quando um objeto é lançado com uma velocidade inicial em um ângulo em relação à horizontal, ele segue uma trajetória parabólica, conhecida como tiro parabólico oblíquo.
Uma das principais características do movimento oblíquo é que a velocidade do objeto varia ao longo da trajetória, pois a componente vertical da velocidade é afetada pela gravidade, enquanto a componente horizontal permanece constante, desde que não haja resistência do ar. Além disso, a altura máxima atingida pelo objeto ocorre quando a velocidade vertical se torna zero.
Para descrever o movimento oblíquo, podemos utilizar diversas fórmulas e equações. A equação geral da trajetória para um tiro parabólico oblíquo é dada por y = x * tan(θ) – (g * x^2) / (2 * v^2 * cos^2(θ)), onde y é a altura, x é a distância horizontal, θ é o ângulo de lançamento, v é a velocidade inicial e g é a aceleração da gravidade.
Para resolver problemas envolvendo tiro parabólico oblíquo, é importante conhecer as fórmulas para encontrar a altura máxima, o alcance máximo, o tempo de voo e a velocidade em determinado ponto da trajetória. Essas fórmulas são essenciais para determinar as características do movimento e prever o comportamento do objeto lançado.
Ao compreender as fórmulas e equações envolvidas, é possível calcular diversas características do movimento, como altura máxima, alcance máximo e tempo de voo, tornando-se essencial para a resolução de problemas relacionados a esse tipo de movimento.
Equações para descrever o movimento oblíquo: quais são e como utilizá-las corretamente.
O movimento oblíquo é aquele em que um objeto é lançado com uma certa inclinação em relação à horizontal. Para descrever esse tipo de movimento, utilizamos equações que levam em consideração tanto o movimento na direção horizontal quanto na direção vertical.
As equações mais comuns para descrever o movimento oblíquo são as equações de movimento horizontal e vertical. No movimento horizontal, a equação mais utilizada é x = v0 * cos(θ) * t, onde x é a posição horizontal do objeto, v0 é a velocidade inicial do objeto, θ é o ângulo de lançamento e t é o tempo decorrido.
Na direção vertical, a equação de movimento mais comum é y = v0 * sen(θ) * t – (1/2) * g * t^2, onde y é a posição vertical do objeto, v0 é a velocidade inicial do objeto, θ é o ângulo de lançamento, g é a aceleração da gravidade e t é o tempo decorrido.
Para utilizar corretamente essas equações, é importante ter em mente que o movimento do objeto é independente nas direções horizontal e vertical. Isso significa que podemos tratar cada direção separadamente e depois combinar os resultados para obter a trajetória completa do objeto.
Utilizando corretamente essas equações, podemos analisar com precisão a trajetória do objeto e prever onde ele irá atingir o solo.
Como calcular o alcance de um objeto em movimento?
Para calcular o alcance de um objeto em movimento, como no caso de um tiro parabólico oblíquo, é necessário levar em consideração algumas características e utilizar fórmulas e equações específicas. O tiro parabólico oblíquo é um tipo de movimento em que um objeto é lançado em um ângulo em relação à horizontal, seguindo uma trajetória parabólica.
Uma das principais características desse tipo de movimento é que a única força que atua sobre o objeto é a força gravitacional, o que resulta em uma trajetória parabólica. Para calcular o alcance do objeto, podemos utilizar a seguinte fórmula: R = (v^2 * sin(2θ))/g, onde R representa o alcance, v é a velocidade inicial do objeto, θ é o ângulo de lançamento e g é a aceleração da gravidade.
Para encontrar o alcance, basta substituir os valores conhecidos na fórmula e realizar os cálculos. Por exemplo, se um objeto é lançado com uma velocidade inicial de 20 m/s e um ângulo de lançamento de 30 graus, e a aceleração da gravidade é de 9,8 m/s², podemos calcular o alcance da seguinte maneira:
R = (20^2 * sin(2*30))/9,8 = (400 * sin(60))/9,8 = (400 * √3/2)/9,8 = 200√3/9,8 ≈ 63,99 m
Portanto, o alcance do objeto lançado nessas condições seria de aproximadamente 63,99 metros. É importante lembrar de sempre converter os ângulos para radianos ao utilizar as fórmulas, e de considerar a direção do movimento para determinar o alcance corretamente.
Tiro parabólico oblíquo: características, fórmulas, equações, exemplos
O tiro parabólico oblíquo é um caso particular do movimento de queda livre em que a velocidade inicial do projétil forma um certo ângulo com a horizontal, resultando em um caminho parabólico.
A queda livre é um caso de movimento com aceleração constante, em que a aceleração é a da gravidade, que sempre aponta verticalmente para baixo e tem uma magnitude de 9,8 m / s ^ 2. Não depende da massa do projétil, como Galileu Galilei demonstrou em 1604.
Se a velocidade inicial do projétil é vertical, a queda livre tem uma trajetória reta e vertical, mas se a velocidade inicial é oblíqua, o caminho da queda livre é uma curva parabólica, fato também demonstrado pelo Galileo.
Exemplos de movimento parabólico são o caminho seguido por uma bola de beisebol, a bala disparada por um canhão e o jato de água saindo de uma mangueira.
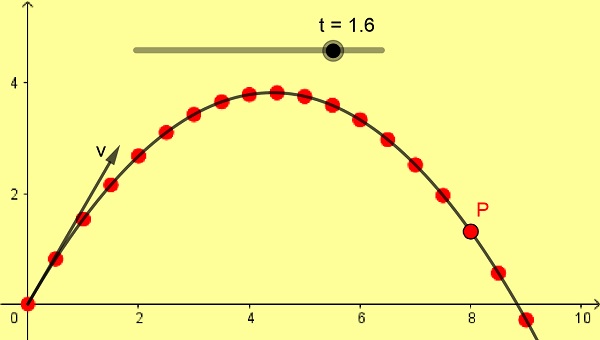
A Figura 1 mostra um tiro parabólico oblíquo de 10 m / s com um ângulo de 60 °. A escala está em metros e as posições sucessivas de P são tomadas com uma diferença de 0,1 s a partir do momento inicial 0 segundos.
Fórmulas
O movimento de uma partícula é completamente descrito se sua posição, velocidade e aceleração são conhecidas como função do tempo.
O movimento parabólico resultante de um tiro oblíquo é a superposição de um movimento horizontal em velocidade constante, mais um movimento vertical com aceleração constante igual à aceleração da gravidade.
As fórmulas que se aplicam ao tiro parabólico oblíquo são aquelas que correspondem a um movimento com aceleração constante a = g , observe que negrito foi usado para indicar que a aceleração é uma quantidade vetorial.
Posição e velocidade
Em um movimento com aceleração constante, a posição depende matematicamente do tempo na forma quadrática.
Se denotamos r (t) a posição no tempo t , r ou a posição no instante inicial, v ou a velocidade inicial, g a aceleração et = 0 como instante inicial, a fórmula que fornece a posição para cada momento do tempo t é :
r (t) = r o + v ou t + ½ g t 2
As letras em negrito na expressão anterior indicam que é uma equação vetorial.
A velocidade em função do tempo é obtida tomando a derivada em relação à posição e o resultado é:
v (t) = v o + g t
E para obter a aceleração em função do tempo, é tomada a derivada da velocidade em relação a t, resultando em:
a (t) = g
Quando o tempo não está disponível, existe uma relação entre velocidade e posição, que é dada por:
v 2 = v ou 2 – 2 g (y – yo)
Equações
Abaixo, encontraremos as equações que se aplicam a um tiro parabólico oblíquo na forma cartesiana.
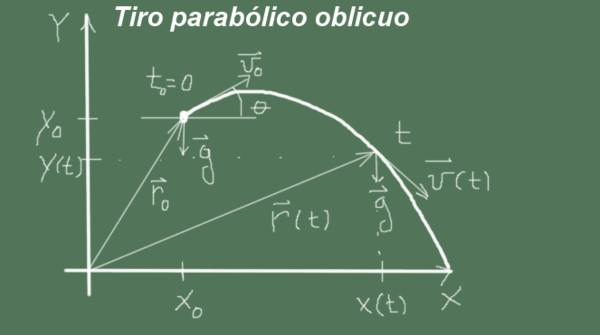
O movimento começa no momento t = 0 com a posição inicial (xo, i) e velocidade de magnitude v o e ângulo θ , ou seja, o vetor de velocidade inicial é (v ou cosθ, v ou sinθ) . O movimento ocorre com aceleração
g = (0, -g).
Equações paramétricas
Se a fórmula vetorial que fornece a posição em função do tempo for aplicada e os componentes forem agrupados e combinados, serão obtidas as equações que fornecem as coordenadas da posição em qualquer momento do tempo t.
x (t) = x o + v ox t
y (t) = y o + v oy t -½ gt 2
Da mesma forma, temos as equações para os componentes de velocidade em função do tempo.
v x (t) = v ox
v e (t) = v o – gt
Onde: v ox = v ou cosθ;v oy = v o senθ
Equação do caminho
y = A x ^ 2 + B x + C
A = -g / (2 v ox ^ 2)
B = (v oy / v ox + gx o / v ox ^ 2)
C = (y o – v oy x o / v ox )
Exemplos
Exemplo 1
Responda às seguintes perguntas:
a) Por que, nos problemas do tiro parabólico, o efeito do atrito com o ar é geralmente negligenciado?
b) A forma do objeto no disparo parabólico é importante?
Respostas
a) Para que o movimento de um projétil seja parabólico, é importante que a força de atrito do ar seja muito menor que o peso do objeto que está sendo jogado.
Se uma bola de cortiça ou algum material leve for lançado, a força de atrito é comparável ao peso e sua trajetória não pode se aproximar de uma parábola.
Pelo contrário, se é um objeto pesado como uma pedra, a força de atrito é desprezível em comparação com o peso da pedra e sua trajetória se aproxima de uma parábola.
b) A forma do objeto lançado também é relevante. Se uma folha de papel na forma de um avião for lançada, seu movimento não será queda livre ou parabólica, pois a forma favorece a resistência do ar.
Por outro lado, se a mesma folha de papel for compactada na forma de uma bola, o movimento resultante será muito semelhante a uma parábola.
Exemplo 2
Um projétil é lançado do solo horizontal com uma velocidade de 10 m / se um ângulo de 60 °. Estes são os mesmos dados com os quais a figura 1. Foi elaborada com os seguintes dados:
a) Instantâneo quando atingir a altura máxima.
b) A altura máxima.
c) A velocidade na altura máxima.
d) A posição e velocidade em 1,6 s.
e) No momento em que ele toca o chão novamente.
f) O alcance horizontal.
Solução a)
A velocidade vertical em função do tempo é
v y (t) = v oy – gt = v ou sinθ – gt = 10 sen60º – 9,8 t = 8,66 – 9,8 t
Quando a altura máxima é atingida, a velocidade vertical é zero por um instante.
8,66 – 9,8 t = 0 ⇒ t = 0,88 s .
Solução b)
A altura máxima é dada pela coordenada e no momento em que essa altura é atingida:
y (0,88s) = I + I t -½ gt ^ 2 = 0 + 8,66 * 0,88-½ 9,8 0,88 ^ 2 =
3,83 m
Portanto, a altura máxima é de 3,83 m.
Solução c)
A velocidade máxima da altura é horizontal:
v x (t) = v ox = v ou cosθ = 10 cos60º = 5 m / s
Solução d)
A posição em 1,6 s é:
x (1,6) = 5 * 1,6 = 8,0 m
e (1,6) = 8,66 * 1,6-½ 9,8 1,6 2 = 1,31 m
Solução e)
Quando você toca no chão de coordenadas e ele cancela, então:
y (t) = 8,66 * t-½ 9,8 t 2 = 0 ⇒ t = 1,77 s
Solução f)
A faixa horizontal é a coordenada x no momento em que toca o chão:
x (1,77) = 5 * 1,77 = 8,85 m
Exemplo 3
Encontre a equação do caminho com os dados no exemplo 2.
Solução
A equação do caminho paramétrico é:
x (t) = 5 * t
y (t) = 8,66 * t-½ 9,8 t ^ 2
E a equação cartesiana é obtida limpando t do primeiro e substituindo no segundo
y = 8,66 * (x / 5) -½ 9,8 (x / 5) ^ 2
Simplificando:
y = 1,73 x – 0,20 x ^ 2
Referências
- PP Teodorescu (2007). «Cinemática». Sistemas Mecânicos, Modelos Clássicos: Mecânica de Partículas. Springer
- Resnick, Halliday e Krane (2002). Volume de Física 1. Cecsa, México.
- Thomas Wallace Wright (1896). Elementos da Mecânica, incluindo Cinemática, Cinética e Estática. E e FN Spon.
- Wikipedia Movimento parabólico Recuperado de es.wikipedia.org.
- WikipediaMovimento de projétil, recuperado de en.wikipedia.org.