A velocidade angular é uma grandeza física que descreve a rapidez com que um objeto gira em torno de um eixo. Ela é medida em radianos por segundo (rad/s) e é fundamental para o estudo do movimento circular. A fórmula para o cálculo da velocidade angular é dada pela razão entre o ângulo percorrido em determinado intervalo de tempo e o tempo decorrido. Neste artigo, exploraremos mais sobre a definição da velocidade angular, sua fórmula de cálculo e apresentaremos alguns exercícios para ajudar na compreensão e fixação do conteúdo.
Fórmula da velocidade angular: como calcular a rotação de um objeto em movimento.
A velocidade angular é uma grandeza física que mede a rapidez com que um objeto está girando em torno de um eixo. Para calcular a velocidade angular de um objeto em movimento, podemos utilizar a fórmula:
Velocidade angular (ω) = Δθ / Δt
Onde Δθ representa a variação do ângulo percorrido pelo objeto e Δt é o intervalo de tempo em que essa rotação ocorreu. A unidade de medida da velocidade angular é rad/s (radianos por segundo).
Para calcular a rotação de um objeto em movimento, basta determinar a variação do ângulo percorrido pelo objeto e o intervalo de tempo em que essa rotação ocorreu. Com esses valores em mãos, podemos aplicar a fórmula da velocidade angular e obter o resultado desejado.
É importante ressaltar que a velocidade angular pode ser tanto positiva quanto negativa, indicando o sentido de rotação do objeto. Uma velocidade angular positiva indica rotação no sentido anti-horário, enquanto uma velocidade angular negativa indica rotação no sentido horário.
Para fixar o conceito, vamos resolver um exercício simples:
Exercício: Um disco gira em torno de seu eixo com uma velocidade angular de 2 rad/s. Se o disco percorre um ângulo de 90 graus em 3 segundos, qual é a velocidade angular média do disco?
Solução: Utilizando a fórmula da velocidade angular, temos que Δθ = 90 graus = (90 * π) / 180 = π/2 rad e Δt = 3 s. Substituindo na fórmula, obtemos:
Velocidade angular média = Δθ / Δt = (π/2) / 3 = π / 6 rad/s
Portanto, a velocidade angular média do disco é de π / 6 rad/s.
O que é velocidade angular e qual sua definição de forma resumida.
A velocidade angular é uma grandeza física que mede a rapidez com que um objeto gira em torno de um eixo. Ela é representada pela letra grega ω (ômega) e sua unidade de medida no Sistema Internacional é radiano por segundo (rad/s).
De forma resumida, a velocidade angular é a taxa de variação do ângulo em relação ao tempo. Ou seja, é a medida da rapidez com que um objeto gira em torno de seu próprio eixo.
A fórmula para calcular a velocidade angular é:
ω = Δθ / Δt
Onde ω é a velocidade angular, Δθ representa a variação do ângulo percorrido e Δt é a variação do tempo decorrido. Para calcular a velocidade angular média, basta dividir a variação do ângulo pelo intervalo de tempo.
Para exemplificar, se um objeto realiza uma rotação de 90 graus em um intervalo de 2 segundos, a velocidade angular média será:
ω = 90° / 2s = 45°/s
Assim, a velocidade angular média do objeto será de 45 graus por segundo.
Em resumo, a velocidade angular é a medida da rapidez com que um objeto gira em torno de um eixo, sendo calculada pela variação do ângulo em relação ao tempo.
Definição, fórmula e unidade da velocidade angular média em um título simples.
Velocidade angular: definição, fórmula, cálculo e exercícios
A velocidade angular é a taxa de variação do ângulo em relação ao tempo. Ela é medida em radianos por segundo e representa a rapidez com que um objeto gira em torno de um ponto.
A velocidade angular média é calculada pela fórmula:
ω = (∆θ / ∆t)
Onde:
ω = velocidade angular média
∆θ = variação do ângulo
∆t = variação do tempo
A unidade da velocidade angular média é radianos por segundo (rad/s).
Agora que você conhece a definição, a fórmula e a unidade da velocidade angular média, pratique com alguns exercícios para fixar o seu entendimento sobre o assunto.
Cálculo da aceleração angular: o passo a passo para determinar a variação da velocidade angular.
Para calcular a aceleração angular, primeiro precisamos entender que a aceleração angular é a taxa de variação da velocidade angular de um objeto em movimento circular. A fórmula para calcular a aceleração angular é dada por:
a = Δω / Δt
Onde a é a aceleração angular, Δω é a variação da velocidade angular e Δt é a variação do tempo. Para determinar a variação da velocidade angular, podemos usar a fórmula:
Δω = ωf – ωi
Onde ωf é a velocidade angular final e ωi é a velocidade angular inicial do objeto. Por fim, para calcular a aceleração angular, basta substituir os valores na fórmula e realizar a operação matemática.
Por exemplo, se um objeto parte do repouso e após 5 segundos atinge uma velocidade angular de 10 rad/s, podemos calcular a aceleração angular da seguinte maneira:
Δω = 10 – 0 = 10 rad/s
Δt = 5 s
a = 10 / 5 = 2 rad/s²
Portanto, a aceleração angular do objeto é de 2 rad/s². Este é o passo a passo para determinar a variação da velocidade angular e calcular a aceleração angular de um objeto em movimento circular.
Velocidade angular: definição, fórmula, cálculo e exercícios
A velocidade angular é uma medida da velocidade de rotação e é definida como o ângulo que gira o vetor de posição do objeto em rotação, por unidade de tempo.É uma magnitude que descreve muito bem o movimento de uma infinidade de objetos que giram constantemente por toda parte: CDs, rodas de carros, máquinas, Terra e muito mais.
Um esquema do “olho de Londres” pode ser visto na figura a seguir. Representa o movimento de um passageiro representado pelo ponto P, que segue o caminho circular, chamado c:
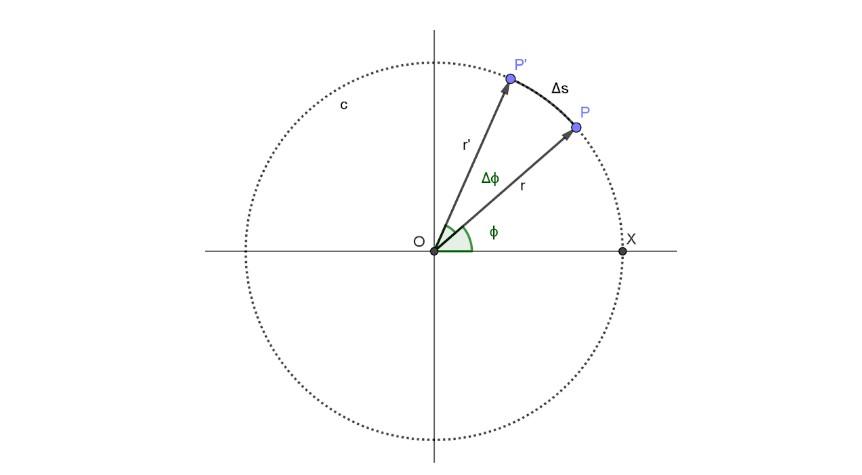
O passageiro ocupa a posição P no momento te posição angular correspondente a esse momento é ϕ.
Desde o tempo t decorre um período de tempo Δt. Nesse período, a nova posição do passageiro pontual é P ‘e a posição angular aumentou em um ângulo Δϕ.
Como é calculada a velocidade angular?
Para as magnitudes de rotação, as letras gregas são muito usadas, a fim de diferenciá-las das magnitudes lineares. Então, inicialmente, a velocidade angular média ω m é definida como o ângulo percorrido em um determinado período de tempo.
Então a razão Δϕ / Δt representará a velocidade angular média ω m entre os momentos t e t + Δt.
Se você deseja calcular a velocidade angular apenas no momento t, será necessário calcular a razão Δϕ / Δt quando Δt 0:

Relação entre velocidade linear e angular
A velocidade linear v , é a razão entre a distância percorrida e o tempo necessário para percorrê-la.
Na figura acima, o arco percorrido é Δs. Mas esse arco é proporcional ao ângulo percorrido e ao raio, cumprindo a seguinte relação, válida desde que Δϕ seja medida em radianos :
Δs = r · Δϕ
Se dividirmos a expressão anterior entre o intervalo de tempo Δt e tomarmos o limite quando Δt 0,>
v>
Movimento de rotação uniforme

Um movimento de rotação é uniforme se, a qualquer momento observado, o ângulo percorrido for o mesmo no mesmo período de tempo.
Se a rotação for uniforme, a velocidade angular a qualquer momento coincide com a velocidade angular média.

Além disso, quando uma volta completa é realizada, o ângulo percorrido é 2π (equivalente a 360º). Portanto, em uma rotação uniforme, a velocidade angular ω está relacionada ao período T, pela seguinte fórmula:

f = 1 / T
Ou seja, em uma rotação uniforme, a velocidade angular está relacionada à frequência por:
ω = 2π ・ f
Exercícios de velocidade angular resolvidos
Exercício 1
As cabines da grande roda rotativa conhecida como ” London Eye ” se movem lentamente. A velocidade das cabines é de 26 cm / se a roda tem 135 m de diâmetro.
Com esses dados, calcule:
i) A velocidade angular da roda
ii) A frequência de rotação
iii) O tempo que leva para uma cabine virar completamente.
Respostas:
i) A velocidade v em m / s é: v = 26 cm / s = 0,26 m / s.
O raio tem metade do diâmetro: r = (135 m) / 2 = 67,5 m
v = r ・ ω => ω = v / r = (0,26 m / s) / (67,5 m) = 0,00385 rad / s
ii) ω = 2π ・ f => f = ω / 2π = (0,00385 rad / s) / (2π rad) = 6,13 x 10 -4 voltas / s
f = 6,13 x 10 ^ -4 volta / s = 0,0368 volta / min = 2,21 volta / hora.
iii) T = 1 / f = 1 / 2,21 volta / hora = 0,45311 hora = 27 min 11 seg
Exercício 2
Um carro de brinquedo se move em uma pista circular de 2m de raio. Em 0 s, sua posição angular é 0 rad, mas após um tempo t, sua posição angular é dada por:
φ (t) = 2 · t
Determine:
i) A velocidade angular
ii) Velocidade linear a qualquer momento.
Respostas:
i) A velocidade angular é aquela derivada da posição angular: ω = φ ‘(t) = 2.
Ou seja, o carro de brinquedo sempre tem velocidade angular constante igual a 2 rad / s.
ii) A velocidade linear do carro é: v = r · ω = 2 m · 2 rad / s = 4 m / s = 14,4 Km / h
Exercício 3
O mesmo carro do exercício anterior começa a parar. Sua posição angular em função do tempo é dada pela seguinte expressão:
φ (t) = 2 · t – 0,5 · t 2
Determine:
i) Velocidade angular a qualquer momento
ii) velocidade linear a qualquer momento
iii) O tempo que leva para parar a partir do momento em que começa a desacelerar
iv) O ângulo percorrido
v) distância percorrida
Respostas:
i) A velocidade angular é aquela derivada da posição angular: ω = φ ‘(t)
ω (t) = φ ‘(t) = (2 · t – 0,5 · t 2 )’ = 2 – t
ii) A velocidade linear do carro a qualquer momento é dada por:
v (t) = r · ω (t) = 2 · (2 - t) = 4-2 t
iii) O tempo que leva para parar a partir do momento em que começa a desacelerar é determinado pelo conhecimento do momento em que a velocidade v (t) se torna zero.
v (t) = 4-2 t = 0 => t = 2
Em outras palavras, ele para 2 s depois de começar a frear.
iv) No intervalo de 2s desde o momento em que começa a frear até parar, um ângulo dado por φ (2) é percorrido:
φ (2) = 2 · 2 – 0,5 · 2 ^ 2 = 4 – 2 = 2 rad = 2 x 180 / π = 114,6 graus
v) No intervalo de 2 s desde o momento em que começa a frear até parar, a distância s é dada por:
s = r · · = 2m · 2 rad = 4 m
Exercício 4
As rodas de um carro têm 80 cm de diâmetro. Se o carro viajar a 100 km / h. Encontre: i) a velocidade angular de rotação das rodas, ii) a frequência de rotação das rodas, iii) O número de voltas que a roda realiza em um curso de 1 hora.
Respostas:
i) Antes de tudo, vamos converter a velocidade do carro de Km / ham / s
v = 100 Km / h = (100 / 3,6) m / s = 27,78 m / s
A velocidade angular de rotação das rodas é dada por:
ω = v / r = (27,78 m / s) / (0,4 m) = 69,44 rad / s
ii) A frequência de rotação das rodas é dada por:
f = ω / 2π = (69,44 rad / s) / (2π rad) = 11,05 rotações / s
A frequência de rotação é geralmente expressa em rotações por minuto rpm
f = 11,05 volta / s = 11,05 volta / (1/60) min = 663,15 rpm
iii) O número de voltas que a roda realiza em uma hora é calculado sabendo que 1 hora = 60 min e que a frequência é o número de voltas N dividido pelo tempo em que essas N voltas ocorrem.
f = N / t => N = f · t = 663,15 (voltas / min) x 60 min = 39788,7 voltas.
Referências
- Giancoli, D. Física. Princípios com Aplicações. 6ª Edição Prentice Hall. 106-108.
- Resnick, R. (1999). Física Volume 1. Terceira edição em espanhol. México Empresa Editorial Continental SA de CV 67-69.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7th. Edição México Cengage Learning Publishers. 84-85.
- geogebra.org