A velocidade média é um conceito fundamental na física e na matemática que descreve a relação entre a distância percorrida por um objeto e o tempo que ele leva para percorrê-la. Neste artigo, vamos explorar as diferentes fórmulas para calcular a velocidade média, assim como explicar passo a passo como resolver exercícios relacionados a esse tema. Vamos abordar desde a definição da velocidade média até exemplos práticos que ajudarão a entender melhor como aplicar esse conceito em situações do dia a dia.
Fórmula para determinar a velocidade média em um determinado percurso.
Para determinar a velocidade média em um determinado percurso, é necessário utilizar a fórmula matemática que relaciona a distância percorrida e o tempo gasto. A fórmula da velocidade média é representada por:
Velocidade média = distância total / tempo total
Para calcular a velocidade média, basta dividir a distância total percorrida pelo tempo total gasto no percurso. Por exemplo, se um carro percorreu 200 km em 4 horas, a velocidade média pode ser calculada da seguinte forma:
Velocidade média = 200 km / 4 h
Velocidade média = 50 km/h
Portanto, a velocidade média do carro foi de 50 km/h nesse percurso específico. É importante lembrar que a velocidade média é uma medida que indica a rapidez com que um objeto se desloca em relação ao tempo gasto, sendo uma grandeza vetorial que possui direção e sentido definidos.
Dicas para prática de atividades físicas visando o aumento da velocidade média.
Para aumentar a velocidade média durante a prática de atividades físicas, é importante seguir algumas dicas que ajudarão a melhorar o desempenho e alcançar melhores resultados. Aqui estão algumas sugestões para otimizar sua performance:
1. Treinamento de velocidade: Inclua treinos específicos de velocidade no seu programa de exercícios. Realizar sprints, corridas intervaladas e treinos de alta intensidade ajudam a desenvolver a velocidade e a resistência.
2. Fortalecimento muscular: Realize exercícios que visem fortalecer os músculos das pernas, como agachamentos, levantamento de peso e exercícios para os glúteos. Músculos mais fortes ajudam na propulsão e no aumento da velocidade.
3. Alongamento e aquecimento: Antes de iniciar qualquer atividade física, é importante realizar um aquecimento adequado para preparar o corpo para o esforço. Além disso, não se esqueça de alongar os músculos para evitar lesões e melhorar a flexibilidade.
4. Descanso e recuperação: É fundamental dar ao corpo o tempo necessário para se recuperar após os treinos intensos. O descanso adequado é essencial para evitar o overtraining e para permitir que os músculos se reparem e se fortaleçam.
5. Alimentação saudável: Uma dieta equilibrada e rica em nutrientes é essencial para fornecer a energia necessária para os treinos e para a recuperação muscular. Certifique-se de incluir alimentos ricos em proteínas, carboidratos e gorduras saudáveis em sua alimentação.
Seguindo essas dicas e mantendo uma rotina de treinos consistente, você estará no caminho certo para aumentar sua velocidade média e melhorar seu desempenho nas atividades físicas. Lembre-se de sempre consultar um profissional de educação física para orientações personalizadas e ajustes no treinamento.
Qual a velocidade média em m/s de alguém que caminha 1,8km em 25min?
A velocidade média de alguém que caminha 1,8km em 25min pode ser calculada utilizando a fórmula de velocidade média, que é VM = ΔS/Δt, onde VM é a velocidade média, ΔS é a variação da distância percorrida e Δt é a variação do tempo gasto.
No caso em questão, a distância percorrida foi de 1,8km e o tempo gasto foi de 25min. Para converter minutos para horas, dividimos por 60, ou seja, 25min/60 = 0,4167h. Agora, podemos substituir os valores na fórmula: VM = 1,8km / 0,4167h = 4,32 km/h.
Para converter a velocidade de km/h para m/s, basta multiplicar por 1000/3600, já que 1km = 1000m e 1h = 3600s. Portanto, a velocidade média de alguém que caminhou 1,8km em 25min é de 1,2 m/s.
É importante lembrar que a velocidade média é uma grandeza vetorial, ou seja, possui direção e sentido. Neste caso, como estamos lidando com uma distância escalar, a velocidade média é apenas um valor numérico que representa a relação entre a distância percorrida e o tempo gasto.
Descubra a velocidade média de uma pessoa caminhando 1500 m em 20 minutos.
A velocidade média é a razão entre a distância percorrida e o tempo gasto para percorrê-la. Para calcular a velocidade média de uma pessoa caminhando 1500 m em 20 minutos, basta dividir a distância pelo tempo.
A fórmula para calcular a velocidade média é:
Velocidade média = Distância / Tempo
No caso do nosso exemplo, a distância é de 1500 m e o tempo é de 20 minutos. Para obter a velocidade média, basta substituir os valores na fórmula:
Velocidade média = 1500 m / 20 min
Para facilitar o cálculo, é importante transformar o tempo para horas. Como 1 hora possui 60 minutos, temos que 20 minutos equivalem a 20/60 = 1/3 horas. Substituindo na fórmula:
Velocidade média = 1500 m / (1/3) h = 1500 m x 3 = 4500 m/h
Portanto, a velocidade média da pessoa caminhando 1500 m em 20 minutos é de 4500 m/h.
Velocidade média: fórmulas, como calcular e resolver exercícios
A velocidade média para uma partícula em movimento é definida como a razão entre a variação da posição que ela experimenta e o intervalo de tempo usado na mudança.A situação mais simples é aquela em que a partícula se move ao longo de uma linha reta representada pelo eixo x.
Suponha que o objeto em movimento ocupe as posições x 1 e x 2 nos tempos t 1 e t 2 respectivamente. A definição de velocidade média v m é representada matematicamente da seguinte maneira:

As unidades de v m no Sistema Internacional são metros / segundo (m / s). Outras unidades de uso comum que aparecem em textos e dispositivos móveis são: km / h, cm / s, milhas / h, pés / se mais, desde que tenham a forma duração / tempo.
A letra grega “Δ” é lida como “delta” e é usada para indicar brevemente a diferença entre duas quantidades.
Características da velocidade média do vetor v m

A velocidade média é um vetor, pois está relacionada à mudança de posição, que por sua vez é conhecida como vetor de deslocamento .
Essa qualidade é representada em negrito ou por uma seta acima da letra que designa a magnitude. No entanto, em uma dimensão, a única direção possível é a do eixo x e, portanto, a notação vetorial pode ser dispensada.
Como os vetores têm magnitude, direção e sentido, uma análise inicial da equação indica que a velocidade média terá a mesma direção e direção que o deslocamento.
Imagine a partícula de exemplo se movendo ao longo de uma linha reta. Para descrever seu movimento, é necessário indicar um ponto de referência, que será a “origem” e será indicado como O.
A partícula pode se afastar ou se aproximar de O, para a esquerda ou para a direita. Também pode levar um tempo longo ou curto para chegar a uma determinada posição.
As magnitudes mencionadas: posição, deslocamento, intervalo de tempo e velocidade média, descrevem o comportamento da partícula enquanto se move. É sobre as magnitudes cinemáticas .
Para distinguir as posições ou locais à esquerda de O, o sinal (-) é usado e os que estão à direita de O ostentam o sinal (+).
A velocidade média possui uma interpretação geométrica que pode ser vista na figura a seguir. É a inclinação da linha que passa pelos pontos P e Q. Ao cortar na posição vs. curva. tempo em dois pontos, é uma linha secante .

Os sinais de velocidade média
Para a análise a seguir, deve-se levar em consideração que t 2 > t 1 . Ou seja, o próximo momento é sempre maior que o atual. Dessa forma, t 2 – t 1 é sempre positivo, o que geralmente faz sentido diariamente.
Então o sinal da velocidade média será determinado pelo de x 2 – x 1 . Observe que é importante esclarecer onde está o ponto O – a origem -, pois esse é o ponto no qual se diz que a partícula vai “para a direita” ou “para a esquerda”.
“Avançar” ou “Voltar”, como o leitor preferir.
Se a velocidade média for positiva, significa que, em média, o valor de ” x ” aumenta com o tempo, embora isso não signifique que possa ter diminuído em algum momento do período considerado – Δt -.
No entanto, em termos globais, no final dos tempos Δt , ela terminou com uma posição maior do que tinha no início. Os detalhes do movimento são ignorados nesta análise.
E se a velocidade média for negativa? Bem, significa que a partícula termina com uma coordenada menor do que aquela com a qual começou. Ele se moveu para trás. Vejamos alguns exemplos numéricos:
Exemplo 1 : Dadas as posições inicial e final indicadas, indique o sinal da velocidade média. Para onde a partícula se moveu globalmente?
a) x 1 = 3 m; x 2 = 8 m
Resposta : x 2 – x 1 = 8 m – 3 m = 5 m. Velocidade positiva média, a partícula avançou.
b) x 1 = 2 m; x 2 = -3 m
Resposta : x 2 – x 1 = -3 m – 2 m = -5 m. Velocidade negativa média, a partícula se moveu para trás.
c) x 1 = – 5 m; x 2 = -12 m
Resposta : x 2 – x 1 = -12 m – (-5 m) = -7 m. Velocidade negativa média, a partícula se moveu para trás.
d) x 1 = – 4 m; x 2 = 10 m
Resposta : x 2 – x 1 = 10 m – (-4m) = 14 m. Velocidade positiva média, a partícula avançou.
A velocidade média pode ser 0? Sim. Desde que o ponto de partida e o ponto de chegada sejam os mesmos. Isso significa que a partícula estava necessariamente em repouso o tempo todo?
Não, isso significa apenas que a viagem foi de ida e volta. Talvez ele tenha viajado rápido ou muito devagar. Por enquanto não é conhecido.
A velocidade média: uma magnitude escalar
Isso nos leva a definir um novo termo: velocidade média . Em Física, é importante distinguir entre magnitudes vetorial e não vetorial: os escalares.
Para a partícula que fez a viagem de ida e volta, a velocidade média é 0, mas poderia ter sido muito rápida ou talvez não. Para conhecê-lo, a velocidade média é definida como:

As unidades de velocidade média são as mesmas que as da velocidade média. A diferença fundamental entre as duas magnitudes é que a velocidade média inclui informações interessantes sobre a direção e a direção da partícula.
Por outro lado, a velocidade média fornece apenas informações numéricas. Com ele, sabe-se quão rápido ou lento a partícula se moveu, mas não se avançou ou retrocedeu. É por isso que é uma magnitude escalar. Como distingui-los, denotando-os? Uma maneira é deixar as letras em negrito para os vetores ou colocando uma pequena seta neles.
E é importante notar que a velocidade média não precisa ser igual à velocidade média. Para a ida e volta, a velocidade média é zero, mas a velocidade média não é. Ambos têm o mesmo valor numérico quando viajam sempre na mesma direção.
Exercício resolvido
Você volta para casa da escola em silêncio a 95 km / h por 130 km. Começa a chover e reduz a velocidade para 65 km / h. Ele finalmente chega em casa depois de dirigir por 3 horas e 20 minutos.
a) A que distância fica sua casa da escola?
b) Qual foi a velocidade média?
Respostas:
a) Alguns cálculos anteriores são necessários:
A viagem é dividida em duas partes, a distância total é:
d = d 1 + d 2 , com d 1 = 130 km


t 2 = 3,33 – 1,37 horas = 1,96 horas
Cálculo de d 2:
d 2 = 65 km / h x 1,96 h = 125,4 km.
A escola é d 1 + d 2 = 255,4 km da casa.
b) Agora você pode encontrar a velocidade média:

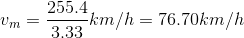
Referências
- Giancoli, D. Física. Princípios com aplicações. Sexta Edição . Prentice Hall. 21-22.
- Resnick, R. (1999). Física Volume 1. Terceira edição em espanhol . México Empresa Editorial Continental SA de CV 20-21.
- Serway, R., Jewett, J. (2008). Física para Ciências e Engenharia. Volume 1. 7 ma . Edição . México Cengage Learning Publishers. 21-23.