Capacità calorifica ed energia interna: teoria, formule ed esperimenti

Início » Ciência » Física » Capacità calorifica ed energia interna: teoria, formule ed esperimenti

La termodinamica è quel ramo della fisica che mette in relazione calore, lavoro e stato dei sistemi; in questo quadro, capacità calorifica ed energia interna sono due pilastri indispensabili per descrivere come l’energia si scambia e come si immagazzina a livello microscopico e macroscopico. In parole semplici, la capacità termica indica quanto “calore” serve per cambiare la temperatura di un corpo, mentre l’energia interna è la somma di tutte le forme di energia delle particelle che lo compongono.

Dietro a queste definizioni ci sono leggi generali come la prima legge della termodinamica (ΔU = Q − W), principi di equilibrio, funzioni di stato e trasformate di Legendre che collegano U, F, H e G, oltre a risultati profondi come le relazioni di Maxwell e quelle reciproche di Onsager. Senza dimenticare la prospettiva storica: dalla vis viva all’equivalente meccanico del calore, fino alle riflessioni sulla forza motrice del fuoco, la strada è stata lunga per arrivare a un linguaggio coerente per calore, lavoro, temperatura, entropia, pressione, volume e potenziale chimico.

Capacità termica: definizione, formule e unità

Con capacità termica (o capacità calorifica) si intende la quantità di calore C che un corpo deve assorbire o cedere per variare la sua temperatura di 1 grado (1 K o 1 °C). Questa grandezza dipende sia dalla massa sia dalla sostanza di cui è fatto l’oggetto: C = m · c, dove c è il calore specifico della sostanza. In alternativa, si può determinare come C = Q / ΔT, cioè rapporto tra calore scambiato e variazione di temperatura.

Nel Sistema Internazionale l’unità è J/K, ma in ambito pratico è diffuso l’uso delle calorie per grado Celsius (cal/°C). È utile ricordare le conversioni: 1 cal = 4,186 J, mentre per quantità maggiori si usano le chilocalorie (1 kcal = 1000 cal ≈ 4186 J). Per le applicazioni domestiche e HVAC compare spesso la BTU (British Thermal Unit): 1 BTU ≈ 252 cal e 1 kcal ≈ 3,968 BTU.

Esempio 1: un corpo di massa 0,8 kg con c = 100 J/(kg·K) ha C = c·m = 100 · 0,8 = 80 J/K. Esempio 2: se un sistema assorbe Q = 2000 J passando da 273 K a 373 K, allora C = Q/ΔT = 2000 / 100 = 20 J/K. In entrambi i casi, la capacità termica cresce con la massa o con il calore specifico.

Attenzione alla differenza concettuale: il calore specifico c è una proprietà della sostanza (non dipende dalla massa), mentre C dipende anche dalla quantità di materia. Per l’acqua liquida, ad esempio, c ≈ 1 cal/(g·°C), molto elevato rispetto a molti solidi come il ferro, che rende l’acqua più “lenta” a riscaldarsi o raffreddarsi.

Calore, calorimetria e conversioni di unità

Il calore è energia in transito dovuta a una differenza di temperatura: fluisce spontaneamente dal corpo più caldo a quello più freddo finché non si raggiunge l’equilibrio termico. I corpi non “contengono” calore; posseggono energia interna. Quando questa energia si trasferisce, parliamo di calore. Nel SI l’unità è il joule (J), ma la caloria è ancora usata in molte applicazioni: 1 cal = 4,1868 J. Anche la BTU è comune: 1 BTU = 252 cal. Da qui la catena utile: 1 kcal = 1 Cal = 1000 cal = 4186 J ≈ 3,968 BTU.

La calorimetria fornisce gli strumenti per misurare scambi di calore. Per il calore sensibile (cambi di temperatura senza cambi di fase) si usa Q = m · c · ΔT. Se invece avviene un cambio di stato, si impiega il calore latente: Q = m · L, con L calore latente di fusione, vaporizzazione, ecc. In un sistema isolato il bilancio energetico impone ∑Q = 0 (il calore ceduto e quello assorbito si compensano).

Un esempio pratico: 1,5 kg d’acqua che passa da 20 °C a 85 °C, con c = 1 cal/(g·°C). Convertendo la massa in grammi (1500 g), Q = m·c·ΔT = 1500 · 1 · 65 = 97.500 cal = 97,5 kcal. La capacità termica di quella porzione d’acqua è C = m·c = 1500 cal/°C. Questi numeri mostrano quanto l’acqua “assorba” calore prima di variare la sua temperatura.

Energia interna: senso fisico, funzioni di stato e potenziali

L’energia interna U di un sistema è la somma di tutte le energie cinetiche e potenziali associate alle sue particelle, comprese eventuali contribuzioni radiative confinate (fotoni intrappolati) e, in un’ottica relativistica/quantistica, anche i contributi legati all’equivalenza massa–energia. In molti contesti classici queste parti possono essere trascurate, ma a livello generale U include energia termica, chimica, energia nucleare ed energia radiante.

Dal punto di vista termodinamico, U è una funzione di stato: la sua variazione dipende solo dagli stati iniziale e finale, non dal percorso. In simboli, ΔU = Uf − Ui. Più in profondità, in sistemi semplici U può essere scritta come U(S, V, N) e le sue trasformate di Legendre costruiscono i potenziali termodinamici: energia libera di Helmholtz F(T, V, N), entalpia H(S, P, N), energia libera di Gibbs G(T, P, N). Queste funzioni fondamentali, insieme alle relazioni di Maxwell, alle equazioni di Bridgman e alle relazioni reciproche di Onsager, costituiscono un vero “manuale” di identità utili per derivare proprietà e risposte del sistema.

Una rappresentazione sintetica delle “quote” di U è utile per orientarsi: energia termica (cinetica microscopica legata a T), energia chimica (soprattutto potenziale elettrica nelle configurazioni elettroniche), energia nucleare (associata alla massa via E = mc²) ed energia radiante (fotoni confinati). La misura di riferimento è in genere fissata nel sistema in quiete (sistema del centro di massa), escludendo le interazioni con l’ambiente.

Componenti tipiche dell’energia interna

Tipo	Descrizione
Energia termica	Cinetica microscopica associata alle variazioni di temperatura.
Energia chimica	Potenziale (soprattutto elettrica) legata a legami e reazioni.
Energia nucleare	Contributo di massa via E = mc² (rilevante in processi nucleari).
Energia radiante	Energia dei fotoni confinati all’interno del sistema.

In termini microscopici, la media su tutte le particelle dà U = ∑Ei, dove ogni Ei è un contributo (cinetico, potenziale, vibrazionale, rotazionale, ecc.). In un gas ideale classico, come vedremo, U dipende solo dalla temperatura. Ma a livello fenomenologico, in molti processi reali (chimici, nucleari) la conversione tra forme diverse di energia interna è ciò che guida riscaldamento, raffreddamento o lavoro utile.

Gas ideali, equipartizione e dipendenza da T

Nei gas ideali, l’energia interna è funzione unicamente della temperatura assoluta T. Grazie al principio di equipartizione, ogni grado di libertà quadratico contribuisce con (1/2)kBT per particella. Per n moli, con R = NA·kB, si ottiene ΔU = (L/2) · n · R · ΔT, dove L è il numero di gradi di libertà attivi.

• Gas monoatomico (He, Ne, Ar): L = 3 (sole traslazioni) ⇒ ΔU = (3/2) n R ΔT.
• Gas biatomico (H2, N2, O2, CO, Cl2): a temperatura ordinaria L ≈ 5 (3 traslazioni + 2 rotazioni) ⇒ ΔU = (5/2) n R ΔT.
• Gas poliatomico (SO2, H2O, CH4…): in molte condizioni L ≈ 6 (3 traslazioni + 3 rotazioni) ⇒ ΔU = 3 n R ΔT. Con l’attivazione dei modi vibrazionali, L può aumentare con la temperatura.

Per i gas ideali monoatomici vale anche la ben nota relazione con stato pV: in condizioni opportune, U = (3/2) pV (per stati corrispondenti). A livello di momenti, l’equipartizione implica per ciascun asse ⟨mvx²/2⟩ = (1/2)kBT, e analogamente sugli altri, così che la somma su x, y, z porta a (3/2)kBT per particella. In moli, la dipendenza lineare di U da T è immediata.

La misura della variazione è spesso espressa anche tramite il calore specifico molare a volume costante cv: ΔU = n · cv · ΔT. Per il monoatomico ideale cv = (3/2)R, per il biatomico ideale (non vibrante) cv = (5/2)R, e per molti poliatomici cv ≈ 3R finché i modi vibrazionali restano congelati.

Esperimenti classici: espansione libera di Joule e effetto Joule–Thomson

Gli esperimenti di Joule hanno chiarito che, per un gas ideale, l’espansione libera non cambia la temperatura: aprendo una paratia tra un serbatoio evacuato e uno ad alta pressione e isolando termicamente, si misura ΔT ≈ 0. Dalla prima legge (Q = 0 e W = 0 per espansione libera), risulta ΔU = 0, quindi per il gas ideale U non dipende dal volume: U = U(T) soltanto.

Con il tampone poroso (esperienza di Joule–Thomson), Joule e Thomson resero possibile misurare piccole variazioni di temperatura in un flusso stazionario che attraversa un materiale poroso tra una pressione iniziale Pi e una finale Pf. Per pareti adiabatiche, il bilancio energetico porta a ΔU = PiVi − PfVf. Per il gas ideale, ancora una volta, si osserva ΔT = 0. Nei gas reali, invece, il segno del coefficiente Joule–Thomson dipende dalla temperatura di inversione: si può riscaldare o raffreddare durante l’espansione a entalpia costante.

Questi risultati rafforzano l’idea che, per i gas ideali, l’energia interna sia funzione della sola T, mentre nei gas reali le interazioni non ideali fanno comparire dipendenze più raffinate.

Prima legge della termodinamica e trasformazioni fondamentali

La prima legge afferma che ΔU = Q − W (lavoro svolto dal sistema). Se il sistema assorbe calore Q e compie lavoro W, la sua energia interna cambia della differenza. A seconda della trasformazione, si ottengono casi notevoli:

• Isoterma (T costante, processo isotermico): per gas ideale ΔU = 0 ⇒ Q = W.
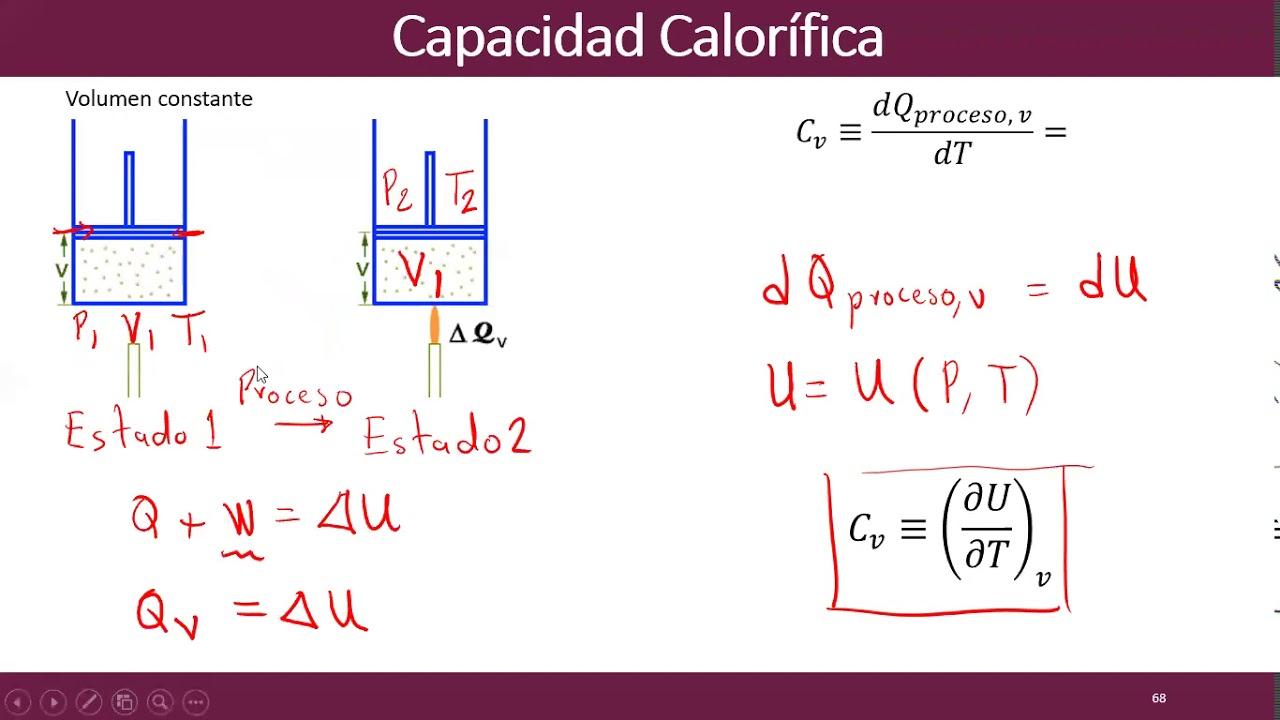
• Isocora (V costante): W = 0 ⇒ ΔU = Q.
• Isobara (p costante): W = p·ΔV ⇒ ΔU = Q − pΔV.
• Adiabatica (Q = 0): ΔU = −W (l’energia interna cala se il sistema compie lavoro, cresce se subisce lavoro).

Nei processi ciclici, il sistema torna allo stato iniziale e quindi ΔU = 0 sull’intero ciclo; di conseguenza, la somma algebrica di calore e lavoro sul ciclo coincide: Qciclo = Wciclo. Questo è il fondamento delle macchine termiche, dove la porzione di calore assorbita che non si trasforma in lavoro viene inevitabilmente rigettata a una sorgente fredda (secondo principio).

Propagazione del calore: conduzione, convezione, irraggiamento

Il trasferimento di calore avviene in tre modi principali. Nella conduzione, la propagazione è per contatto e agitazione microscopica: efficiente nei solidi (es. metalli conduttori), meno in fluidi. Nella convezione, tipica di liquidi e gas, il trasporto è legato a moti di massa dovuti a differenze di densità (correnti convettive). Nell’irraggiamento, il trasferimento avviene tramite onde elettromagnetiche, senza bisogno di mezzo materiale (come la radiazione solare che raggiunge la Terra).

Alcune osservazioni pratiche aiutano l’intuizione: un cucchiaio di alluminio si scalda rapidamente per conduzione; in una pentola d’acqua si instaurano celle convettive che miscelano il fluido; superfici scure assorbono più radiazione rispetto a quelle chiare, influenzando il bilancio radiativo e le velocità di riscaldamento/raffreddamento.

Proprietà, diagrammi e qualità del vapore

La termodinamica distingue tra proprietà estensive (proporzionali alla quantità di materia, come massa, volume, energia) e proprietà intensive (indipendenti dalla quantità, come temperatura, pressione). Diagrammi p–V, T–S e p–T permettono di visualizzare trasformazioni e regioni di fase. Nella regione bifase liquido–vapore, la qualità del vapore (titolo) quantifica la frazione in massa di vapore presente. Le proprietà ridotte (normalizzate a valori critici) facilitano il confronto fra sostanze diverse.

Altre coppie coniugate fondamentali includono temperatura–entropia, pressione–volume, potenziale chimico–numero di particelle. Questi accoppiamenti, insieme alle relazioni di Maxwell, forniscono un set di equazioni incrociate potenti per dedurre derivate parziali difficili da misurare direttamente, chiudendo il cerchio tra proprietà misurabili e potenziali.

Esempi numerici selezionati

Capacità termica da c e m: un blocco di 500 g di sostanza riceve 4000 cal per passare da 20 °C a 70 °C. La capacità è C = Q/ΔT = 4000/50 = 80 cal/°C. Il calore specifico è c = Q/(m·ΔT) = 4000/(500·50) = 0,16 cal/(g·°C).

Flusso di calore: se una sorgente fornisce 50 cal/min per 20 min, il calore totale è Q = 1000 cal. Per un corpo con C = 25 cal/°C, la variazione di temperatura è ΔT = Q/C = 40 °C. Qui si vede come una capacità maggiore smorzi le variazioni di temperatura a parità di calore scambiato.

Energia interna di gas monoatomico: 5 mol a T = 200 K (ad esempio −73 °C). Con ΔU = (3/2) n R ΔT, prendendo R = 8,31 J/(mol·K), si ottiene ΔU = (3/2)·5·8,31·200 ≈ 12.465 J.

Uso di unità pratiche: convertire 1 J/K in cal/°C richiede dividere per 4,184: 1 J/K ≈ 0,24 cal/°C. Viceversa, 1 cal/°C · 4,184 ≈ 4,184 J/K. Tenere a mente 1 BTU = 252 cal aiuta a stimare la potenza termica di condizionatori e scaldacqua.

Cenni storici e quadro teorico

La storia di questi concetti passa dalla vis viva (l’“antica” idea di forza viva) all’equivalente meccanico del calore misurato da Joule, che stabilì il ponte quantitativo tra lavoro meccanico e calore. Carnot interpretò la forza motrice del fuoco, aprendo la strada al secondo principio. Di note capitale sono i lavori di Gibbs sulla eterogeneità e le condizioni d’equilibrio, e l’iconica superficie termodinamica di Maxwell, che aiuta a visualizzare stati e processi. La nozione di entropia come dispersione dell’energia ha poi consolidato il quadro concettuale moderno.

L’impossibilità di macchine a moto perpetuo (di prima e seconda specie) non è un dettaglio, ma una conseguenza delle leggi stesse: la conservazione dell’energia fissa i bilanci (prima legge), mentre l’irreversibilità e la crescita dell’entropia vietano conversioni integrali di calore in lavoro senza “scarti” (seconda legge). In laboratorio e in tecnologia, questo significa che parte del calore deve sempre essere rifiutata a una sorgente fredda.

Osservazioni e casi quotidiani

Alcune intuizioni pratiche collegano i concetti: un gas compresso adiabaticamente aumenta la propria energia interna (e la temperatura), una molla compressa immagazzina più energia interna rispetto a quando è estesa (energia meccanica: energia meccanica), una batteria carica possiede più energia interna di una scarica, e una data massa di vapore ha energia interna maggiore dello stesso sistema in forma di acqua fredda. Queste affermazioni illustrano la varietà di forme di immagazzinamento dell’energia a parità di sostanza.

Esperienze semplici aiutano a distinguere conduzione e capacità termica: una teglia di alluminio “sembra” più fredda al tatto rispetto a una di plastica alla stessa temperatura ambiente per via della maggiore conducibilità (trasferisce calore dalla mano più rapidamente). Un cubetto di ghiaccio si scioglierà più velocemente sull’alluminio proprio per questo motivo, benché le temperature iniziali fossero uguali.

Capacità termica (C = m·c o C = Q/ΔT) con unità J/K o cal/°C e convertibilità con BTU nel pratico; energia interna come funzione di stato che in un gas ideale dipende solo dalla temperatura (ΔU = (L/2) n R ΔT o ΔU = n cv ΔT); prima legge (ΔU = Q − W) a governare trasformazioni isoterme, isocore, isobare e adiabatiche; calorimetria con Q = m c ΔT e calori latenti Q = m L; e un contesto teorico che include potenziali termodinamici, relazioni di Maxwell, reciprocità di Onsager e utili identità di Bridgman. Con questi strumenti si può leggere, con occhio coerente, tanto l’operare di una macchina termica quanto la dinamica termica degli oggetti di tutti i giorni.