Como converter frações impróprias em números mistos na quarta série

Início » Ciência » Matemática » Como converter frações impróprias em números mistos na quarta série

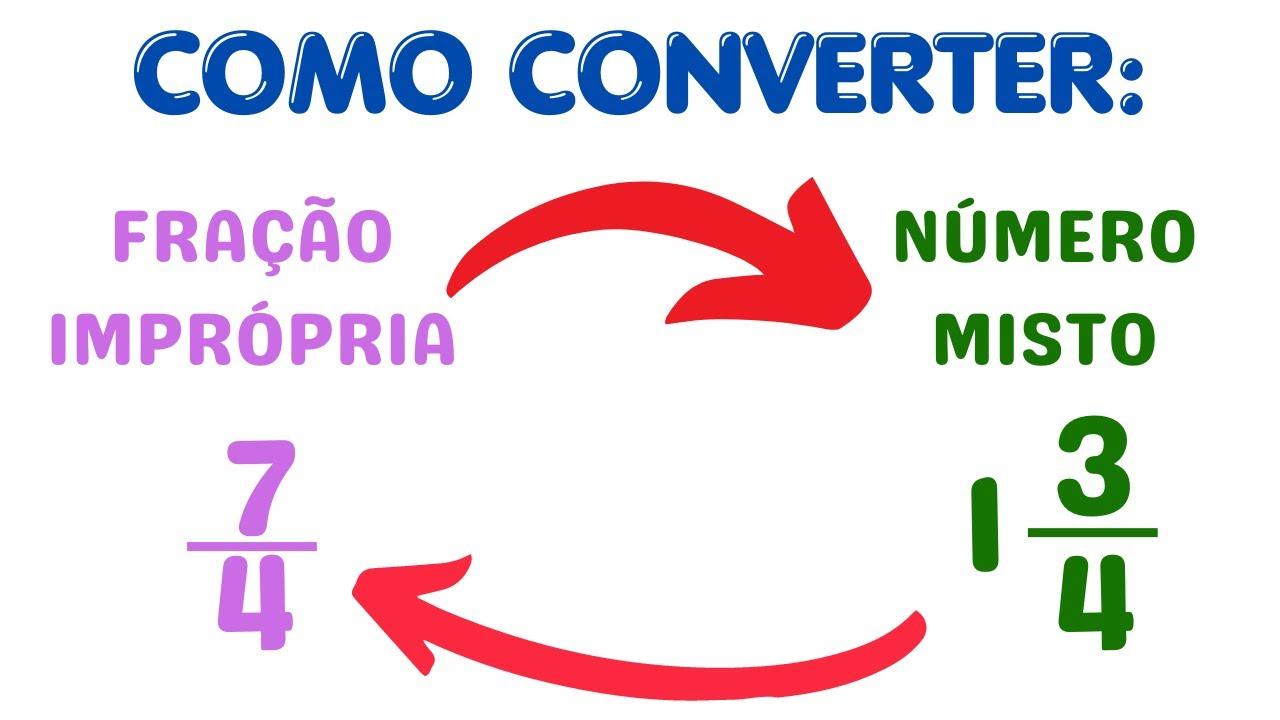
Aprender a converter frações impróprias em números mistos na quarta série é um passo importante para ganhar fluência em frações e no raciocínio proporcional. Quando entendemos como separar a parte inteira da parte fracionária, a leitura e a comparação de quantidades ficam muito mais simples, e isso ajuda tanto nos exercícios quanto no dia a dia.

Antes de colocar a mão na massa, vale lembrar: nem toda fração vira número misto. Somente as frações impróprias, aquelas em que o numerador é maior que o denominador e não representam um número inteiro, podem ser reescritas como número misto. Isso porque o número misto é exatamente a soma de uma quantidade inteira com uma parte fracionária.

Segura essa dica rápida: o conteúdo segue firme e forte logo depois do intervalo de publicidade — pode confiar que tem bastante exemplo prático e explicação direta ao ponto.

Tópicos deste artigo

• Definição de número misto e por que ele facilita a leitura de frações.
• Classificações de frações: própria, aparente e imprópria.
• Método para converter fração imprópria em número misto (e o caminho inverso).
• Exercícios comentados para fixar as ideias.

O que é um número misto?

O número misto, também chamado de fração mista, é a escrita de uma quantidade que possui duas partes: uma inteira e outra fracionária. Ele aparece sempre como um inteiro acompanhado de uma fração própria, como 2 1/3 (lê-se: dois inteiros e um terço). Essa forma explicita o que já está “completo” (a parte inteira) e o que está “pela metade” (a fração), deixando a interpretação mais natural.

Por exemplo, quando dizemos 5 2/7, estamos afirmando que há cinco unidades inteiras e ainda restam duas sétimas partes de outra unidade. Essa visualização ajuda a comparar quantidades e a estimar resultados, especialmente em atividades práticas, como medir, cozinhar ou dividir objetos.

Em resumo, o número misto reescreve uma fração imprópria de maneira mais amigável. Ele não altera o valor da fração, apenas muda a forma de apresentação, tornando a leitura e a compreensão mais acessíveis para estudantes da quarta série.

Tipos de fração

Para dominar a transformação entre fração imprópria e número misto, convém revisar os três tipos clássicos de frações. Conhecer a classificação evita erros e deixa claro quando o número misto é aplicável.

Fração aparente

A fração aparente é aquela que representa um número inteiro. Isso acontece quando o numerador é múltiplo do denominador, ou seja, a divisão “fecha” sem deixar resto: 10/2 = 5, 12/4 = 3, e até -25/5 = -5 são exemplos de frações que, apesar de terem barra, equivalem a inteiros puros.

Note que, por já serem números inteiros, as frações aparentes não se escrevem como número misto. Não há parte fracionária sobressalente para destacar, pois a divisão resulta exatamente em um inteiro, sem restos.

Fração própria

A fração própria é aquela em que o numerador é menor do que o denominador (como 1/2, 3/5, 7/9). Nesse caso, o valor é sempre menor que 1, porque você está pegando menos partes do que o total que compõe uma unidade inteira.

Por ser menor que 1, a fração própria não pode ser representada como número misto. Não existe uma parte inteira a destacar quando o numerador é menor do que o denominador, logo, faz mais sentido mantê-la na forma fracionária simples.

Fração imprópria

A fração imprópria, por sua vez, tem o numerador maior do que o denominador e não representa um número inteiro exato. É nesse tipo de fração que a divisão entre numerador e denominador deixa um resto, mostrando que há uma combinação de partes inteiras mais uma fração.

Exemplos típicos são 7/3, 9/4 e 17/3. Como essas frações superam o valor 1, faz sentido separarmos o que cabe como inteiro e o que sobra como parte fracionária, chegando assim à forma de número misto.

Uma observação importante: a fração aparente (que vira inteiro) não dá origem a número misto; a fração própria (menor que 1) também não. Somente a fração imprópria pode ser reescrita como número misto, pois ela contém pelo menos um inteiro “cheio” mais uma parte.

Leitura complementar sugerida: Como resolver operações com frações. Esse tipo de revisão ajuda a consolidar as transformações descritas aqui.

Dica extra: três erros frequentes ao simplificar frações algébricas costumam nascer de confusões com as classificações acima, então manter esses conceitos afiados vale ouro.

Como transformar uma fração imprópria em um número misto?

O procedimento é direto e funciona sempre que o numerador ultrapassa o denominador sem a divisão ser exata. Faça a divisão do numerador pelo denominador para descobrir quantas partes inteiras cabem; o quociente será a parte inteira e o resto será o novo numerador da fração.

Passo a passo prático: considere 17/3. Dividindo 17 por 3, obtemos quociente 5 e resto 2, pois 3 × 5 = 15 e 17 − 15 = 2. Isso indica que há 5 inteiros formados por terços, e ainda sobram 2 terços.

Com isso, a escrita como número misto fica: 5 2/3. A parte inteira é o quociente e a parte fracionária usa o resto como numerador e mantém o denominador original. Observe que o denominador nunca muda nessa transformação.

Uma boa prática é verificar se a fração da parte fracionária pode ser simplificada. Se o resto e o denominador tiverem algum divisor comum, simplifique para deixar a resposta mais limpa, sempre preservando o mesmo valor.

Outro aspecto relevante é a leitura do número misto resultante. Ao dizer 5 2/3, leia “cinco inteiros e dois terços”. Esse cuidado com a fala ajuda a conectar a representação simbólica ao significado, reforçando o entendimento.

Se você estiver resolvendo uma lista de exercícios, anote sempre a pequena divisão ao lado (o algoritmo da divisão ou a conta de testar múltiplos). Esse registro revela de onde veio a parte inteira e evita trocas entre quociente e resto, que são confusões comuns para quem está começando.

Como transformar um número misto em uma fração imprópria?

Agora vamos no sentido inverso: reescrever um número misto como fração imprópria. A ideia central é juntar a parte inteira com a parte fracionária em uma única fração, preservando o mesmo denominador da fração do número misto.

O método prático pode ser descrito assim: multiplique a parte inteira pelo denominador e some o numerador da fração; o resultado será o novo numerador, mantendo o denominador. Esse cálculo é exatamente a soma da parte inteira “convertida” para o mesmo denominador com a parte fracionária.

Exemplo rápido com 5 2/3: 5 × 3 = 15; somando o numerador, 15 + 2 = 17. Logo, 5 2/3 = 17/3. Note como o processo desfaz o que fizemos antes, voltando à fração imprópria inicial.

Esse raciocínio funciona para qualquer número misto, inclusive quando a fração puder ser simplificada depois. Simplificar no final continua sendo uma boa prática, desde que você não altere indevidamente o denominador durante o processo.

Reforce com leitura correta: “cinco inteiros e dois terços” e “dezessete terços” para a mesma quantidade fortalece a noção de equivalência. A linguagem oral é uma aliada forte no entendimento de frações, especialmente nessa etapa escolar.

Exemplos comentados e observações didáticas

Vamos retomar alguns exemplos para consolidar. Para 17/3, já vimos que o número misto correspondente é 5 2/3, pois há cinco grupos completos de terços e uma parte fracionária de dois terços.

Considere 9/4: dividindo 9 por 4, o quociente é 2 e o resto é 1. Então, 9/4 = 2 1/4. Perceba que o denominador 4 foi preservado na parte fracionária, como deve ser.

Agora, 7/3: 7 dividido por 3 rende quociente 2 e resto 1. Assim, 7/3 = 2 1/3. Se você quiser voltar para a fração imprópria, multiplique a parte inteira (2) por 3 e some 1: 2 × 3 + 1 = 7; denomine por 3 e pronto.

E quanto às frações aparentes? Tome 12/4: essa fração já é igual a 3. Não há resto; por isso, não existe motivo para escrever como número misto. O mesmo vale para 10/2 (igual a 5) e -25/5 (igual a -5).

Se pintar uma fração própria, como 3/5 ou 2/7, lembre: não vira número misto, porque é menor do que 1. O mais adequado é deixar na forma fracionária, eventualmente simplificada, se der.

Exercícios resolvidos

Questão 1. Dada uma fração imprópria, assinale a alternativa que apresenta sua forma como número misto. Para chegar à resposta, faça a divisão do numerador pelo denominador e identifique a parte inteira (quociente) e a parte fracionária (resto/denominador).

Resolução: Suponha a fração 14/5. Dividindo 14 por 5, obtemos quociente 2 e resto 4. Logo, 14/5 = 2 4/5. Portanto, a opção com 2 4/5 está correta.

Alternativa C. Foi a que trouxe o número misto 2 4/5. Critério usado: divisão com identificação de quociente (parte inteira) e resto (novo numerador) mantendo o denominador. Essa é a estratégia padrão sempre que a fração for imprópria e não aparente.

Para conferir, monte a conta inversa: 2 4/5 = (2 × 5 + 4)/5 = 14/5. Quando a ida e a volta batem, a conversão está correta, o que elimina dúvidas no momento de marcar a alternativa.

Questão 2. Escolha a alternativa que representa o número misto dado como fração imprópria simplificada. A técnica consiste em somar a parte inteira à fração convertendo para o mesmo denominador, isto é, multiplicando o inteiro pelo denominador e somando o numerador.

Resolução: Se o número misto for, por exemplo, 3 1/4, então 3 × 4 = 12; 12 + 1 = 13, logo 3 1/4 = 13/4. Depois, verifique se há simplificação possível. Neste caso, não há.

Alternativa E. Foi a que apresentou a fração 13/4. O raciocínio se aplica a qualquer número misto: inteiro × denominador + numerador; mantenha o denominador ao final.

Erros comuns e como evitá-los

Um deslize frequente é confundir resto com denominador. Na conversão de fração imprópria para número misto, o resto vira o novo numerador, enquanto o denominador permanece igual ao da fração original.

Outro erro é tentar transformar frações próprias em números mistos. Lembre-se: se o numerador for menor que o denominador, não há parte inteira. Essa transformação simplesmente não se aplica.

Também ocorre de chamar fração aparente de número misto. Se a divisão for exata, temos um inteiro, e não um misto. Nada de inventar uma parte fracionária onde não há resto.

Por fim, há quem esqueça de simplificar a fração residual na forma mista, quando possível. Simplificar deixa a resposta mais elegante e costuma ser exigência nas correções, desde que não altere o valor.

Dicas pedagógicas para a quarta série

Na prática de sala, trabalhar com representações visuais (como círculos ou retângulos divididos em partes iguais) ajuda muito. Mostrar cinco círculos completos e, ao lado, dois terços de outro círculo ilustra lindamente o 5 2/3, conectando a conta ao significado.

Ao explicar a divisão, vale resgatar o algoritmo tradicional com quociente e resto. Essa ponte entre aritmética e frações diminui o estranhamento e cria um procedimento que o estudante repete com confiança.

Levar o aluno a verbalizar “cinco inteiros e dois terços” e “dezessete terços” para a mesma quantidade fortalece a noção de equivalência. A linguagem oral é uma aliada forte no entendimento de frações, especialmente nessa etapa escolar.

Listas curtas de exercícios com feedback imediato funcionam bem. Inclua casos de fração imprópria, própria e aparente para que o estudante decida quando (e quando não) aplicar a forma mista.

Perguntas rápidas para checar o entendimento

1) Toda fração vira número misto? Não. Apenas as frações impróprias que não são aparentes, pois há resto ao dividir numerador por denominador.

2) O que fazer com o denominador na conversão para número misto? Ele é mantido na parte fracionária; apenas o numerador muda (passa a ser o resto).

3) Como voltar do misto para a fração imprópria? Multiplique o inteiro pelo denominador, some o numerador, e mantenha o denominador ao final.

4) Frações aparentes viram misto? Não. São números inteiros exatos, sem parte fracionária sobrando.

Mais exemplos de aplicação

Pense em 23/6: 23 ÷ 6 = 3, resto 5. Então 23/6 = 3 5/6. Esse tipo de conversão aparece o tempo todo em problemas de medida, como dividir doces ou pedaços de fita entre grupos.

E 28/7? A conta dá exato: 28 ÷ 7 = 4. Isso é fração aparente, equivalente a 4. Não há número misto aqui, porque não sobra parte fracionária.

Para 11/2, fazemos 11 ÷ 2 = 5, resto 1; logo, 11/2 = 5 1/2. Se você quiser retornar, 5 × 2 + 1 = 11; tudo consistente, uma bela checagem de correção.

Esses exemplos reforçam a regra geral: divisão para obter quociente e resto (na ida) e multiplicação seguida de soma (na volta). Entendido o mecanismo, o processo vira rotina.

Anotações finais e referências do conteúdo

Ao longo do texto, trabalhamos a definição de número misto, as classificações de fração (própria, aparente, imprópria) e os procedimentos de conversão com checagens. Esse repertório cobre o essencial que um estudante da quarta série precisa dominar para lidar com números mistos com segurança.

Como reforço, revisamos exemplos emblemáticos: 10/2, 12/4 e -25/5 como frações aparentes (inteiros); 17/3 como caso-padrão para conversão; e modelos simples para ir e voltar entre as formas. Todos os pontos-chave que você precisa para estudar ou ensinar o tema foram contemplados.

Crédito de imagem: referência editorial a Robert Alford / Shutterstock, citada em materiais didáticos sobre o assunto.

Autor citado em conteúdos correlatos: Raul Rodrigues de Oliveira, professor de Matemática, frequentemente mencionado em materiais explicativos sobre frações.

A mensagem mais importante é: entender quando uma fração é imprópria e distinguir aparente de própria é o que destrava a conversão para número misto. Praticando a divisão para achar quociente e resto, e treinando a volta (inteiro × denominador + numerador), você lê e escreve frações com agilidade, sem tropeços e com sentido.