Uma função bijetiva é uma função que estabelece uma correspondência um para um e sobrejetiva entre dois conjuntos, ou seja, cada elemento do conjunto de partida está associado a um único elemento do conjunto de chegada, e não há elementos do conjunto de chegada que não estejam associados a nenhum elemento do conjunto de partida.
Para determinar se uma função é bijetiva, é necessário verificar se ela é injetiva (cada elemento do conjunto de partida está associado a um único elemento do conjunto de chegada) e sobrejetiva (cada elemento do conjunto de chegada está associado a pelo menos um elemento do conjunto de partida).
Um exemplo de função bijetiva é a função f(x) = 2x – 1, que estabelece uma correspondência um para um entre os números reais.
Para praticar a identificação de funções bijetivas, é possível realizar exercícios que envolvam a análise de gráficos, tabelas ou expressões algébricas de funções. Esses exercícios ajudam a compreender melhor as propriedades das funções bijetivas e a desenvolver habilidades de identificação e análise de funções.
Exemplos de funções bijetoras: entenda o conceito e suas aplicações na matemática.
Uma função bijetiva, também conhecida como função bijetora, é uma função que estabelece uma relação de correspondência um para um e sobrejetora entre dois conjuntos. Isso significa que cada elemento do conjunto de partida está associado a um único elemento do conjunto de chegada, e que nenhum elemento do conjunto de chegada está sem correspondência.
Para uma função ser considerada bijetiva, ela deve ser ao mesmo tempo injetora e sobrejetora. Uma função é injetora quando cada elemento do conjunto de partida está associado a um único elemento do conjunto de chegada. E uma função é sobrejetora quando todo elemento do conjunto de chegada possui pelo menos uma correspondência no conjunto de partida.
Um exemplo simples de função bijetiva é a função f(x) = 2x, onde o conjunto de partida é o conjunto dos números reais e o conjunto de chegada é o conjunto dos números reais não negativos. Nessa função, cada número real x possui uma única imagem, que é o dobro de x. Além disso, todo número real não negativo possui pelo menos uma pré-imagem.
Outro exemplo de função bijetiva é a função f(x) = x + 3, onde o conjunto de partida é o conjunto dos números reais e o conjunto de chegada é o conjunto dos números reais. Nessa função, cada número real possui uma única imagem, que é o número x somado a 3. E todo número real possui pelo menos uma pré-imagem.
As funções bijetivas são muito importantes na matemática, pois permitem estabelecer relações biunívocas entre conjuntos. Elas são utilizadas em diversas áreas da matemática, como na teoria dos conjuntos, na teoria dos números e na análise matemática.
Em resumo, uma função bijetiva é aquela que estabelece uma correspondência um para um e sobrejetora entre dois conjuntos. Ela é ao mesmo tempo injetora e sobrejetora, garantindo que cada elemento do conjunto de partida tenha uma única correspondência no conjunto de chegada, e que nenhum elemento do conjunto de chegada fique sem correspondência.
Tutorial completo sobre como criar uma função bijetora em passos simples e práticos.
Uma função bijetora é uma função que é tanto injetora quanto sobrejetora, ou seja, cada elemento do domínio está associado a um único elemento do contradomínio e cada elemento do contradomínio está associado a um único elemento do domínio. Neste tutorial, vamos aprender como criar uma função bijetora em passos simples e práticos.
O que é uma função bijetiva?
Uma função bijetora é uma função que estabelece uma correspondência um para um entre os elementos do domínio e do contradomínio. Isso significa que cada elemento do domínio é mapeado para um único elemento do contradomínio, e vice-versa.
Como criar uma função bijetora?
Para criar uma função bijetora, siga os seguintes passos:
- Defina o domínio e o contradomínio da função: Escolha quais serão os conjuntos de elementos que serão utilizados na função.
- Estabeleça a correspondência entre os elementos do domínio e do contradomínio: Associe cada elemento do domínio a um único elemento do contradomínio e vice-versa.
- Verifique se a função é injetora: Certifique-se de que cada elemento do domínio está associado a um único elemento do contradomínio.
- Verifique se a função é sobrejetora: Certifique-se de que cada elemento do contradomínio está associado a pelo menos um elemento do domínio.
Exemplo de função bijetiva:
Vamos criar uma função bijetora que associa os números naturais pares aos números inteiros positivos. Para isso, podemos definir a função f(x) = 2x. Esta função é injetora, pois cada número par é associado a um único número inteiro positivo, e é sobrejetora, pois cada número inteiro positivo tem pelo menos um número par associado a ele.
Exercícios:
- Crie uma função bijetora que associe os números reais positivos aos números reais negativos.
- Verifique se a função f(x) = x^2 é bijetora.
Agora que você aprendeu como criar uma função bijetora, você pode praticar mais exemplos e exercícios para aprimorar seus conhecimentos. Lembre-se de que uma função bijetora é uma função que estabelece uma correspondência um para um entre os elementos do domínio e do contradomínio.
Identificando se uma função é bijetiva: passo a passo para determinar sua biunivocidade.
Uma função é considerada bijetiva quando cada elemento do conjunto de partida está relacionado a um único elemento do conjunto de chegada e vice-versa, ou seja, é uma função injetora e sobrejetora.
Para determinar se uma função é bijetiva, siga os seguintes passos:
1. Verifique se a função é injetora: isso significa que cada elemento do conjunto de partida está relacionado a um único elemento do conjunto de chegada. Para isso, verifique se não existem dois elementos diferentes no conjunto de partida que são mapeados para o mesmo elemento no conjunto de chegada.
2. Verifique se a função é sobrejetora: isso significa que todos os elementos do conjunto de chegada têm pelo menos um elemento correspondente no conjunto de partida. Para isso, verifique se não há elementos no conjunto de chegada que não sejam mapeados por nenhum elemento do conjunto de partida.
Se a função passar por esses dois testes e for tanto injetora quanto sobrejetora, então ela é uma função bijetiva.
Um exemplo de função bijetiva é a função f(x) = 2x, onde cada elemento do conjunto de partida é mapeado para um único elemento do conjunto de chegada e vice-versa.
Agora, vamos praticar com alguns exercícios para determinar se as seguintes funções são bijetivas:
1. f(x) = x²
2. g(x) = 3x + 1
Ao seguir os passos acima, você será capaz de identificar se uma função é bijetiva e compreender melhor esse conceito matemático.
Gráfico de função Bijetora: características e representação visual em um plano cartesiano.
Uma função bijetora é uma função que estabelece uma relação de um para um entre dois conjuntos. Isso significa que cada elemento do conjunto de origem está associado a um único elemento do conjunto de destino, e vice-versa. Em outras palavras, uma função bijetora é tanto injetora quanto sobrejetora.
Uma das maneiras de visualizar uma função bijetora é através do seu gráfico em um plano cartesiano. No gráfico de uma função bijetora, cada elemento do conjunto de origem é representado no eixo x, enquanto cada elemento correspondente do conjunto de destino é representado no eixo y. Como a função é bijetora, cada elemento do eixo x está associado a um único elemento do eixo y, e vice-versa.
Características de um gráfico de função bijetora incluem uma representação biunívoca entre os conjuntos de origem e destino, sem pontos sobrepostos ou lacunas. Além disso, o gráfico de uma função bijetora é simétrico em relação à reta y = x, o que significa que a função é invertível.
Para representar visualmente uma função bijetora em um plano cartesiano, basta plotar os pontos correspondentes de cada par ordenado (x, y) de acordo com a relação estabelecida pela função. O gráfico resultante será uma curva suave e contínua, sem interrupções ou repetições.
Em resumo, um gráfico de função bijetora é uma representação visual que mostra a relação de um para um entre dois conjuntos, sem sobreposições ou lacunas. Ele é simétrico em relação à reta y = x e pode ser facilmente identificado pela sua característica biunívoca. Este tipo de função é muito utilizado em matemática e em diversas outras áreas, devido à sua propriedade de estabelecer uma correspondência única entre elementos de conjuntos distintos.
Função bijetiva: o que é, como é feito, exemplos, exercícios
Uma função bijetiva é aquela que atende à dupla condição de ser injetiva e superjetiva . Ou seja, todos os elementos do domínio tem uma imagem única no codomain, e por sua vez o codomain é igual a função rank ( R f ).
É realizado quando se considera uma relação biunívoca entre os elementos do domínio e o codomain.Um exemplo simples é a função F: R → R definida pela linha F (x) = x

Observa-se que, para cada valor do domínio ou conjunto de partida (ambos os termos se aplicam igualmente), existe apenas uma imagem no codomain ou conjunto de chegada. Além disso, não há nenhum elemento do codomain que não seja uma imagem.
Desta forma, F: R → R definido pela linha F (x) = x é bijetivo
Como é feita uma função bijetiva?
Para responder a isso, é necessário esclarecer os conceitos relacionados à Injetividade e Super atividade de uma função , além dos critérios para condicionar as funções para adaptá-las aos requisitos.
Injeção de uma função
Uma função é injetiva quando cada um dos elementos de seu domínio está relacionado a um único elemento do codomain. Um elemento do codomain pode ser apenas uma imagem de um único elemento do domínio; dessa forma, os valores da variável dependente não podem ser repetidos.
Para considerar uma função injetiva , o seguinte deve ser cumprido:
∀ x 1 ≠ x 2 ⇒ F (x 1 ) ≠ F (x 2 )
Super atividade de uma função
Uma função é classificada como superjetiva , se cada elemento de seu codomain for uma imagem de pelo menos um elemento do domínio.
Para considerar uma função como superjetiva, o seguinte deve ser cumprido:
Seja F: D f → C f
∀ b ℮ C f E a ℮ D f / F (a) = b
Esta é a maneira algébrica de estabelecer que, para cada “b” que pertence a C f, existe um “a” que pertence a D f, de modo que a função avaliada em “a” é igual a “b”.
Função Condicionamento
Às vezes, uma função que não é bijetiva pode sofrer certas condições. Essas novas condições podem transformá-lo em uma função bijetiva. Todos os tipos de modificações no domínio e no co-domínio da função são válidos, onde o objetivo é cumprir as propriedades de injetividade e atividade excessiva no relacionamento correspondente.
Exemplos: exercícios resolvidos
Exercício 1
Seja a função F: R → R definida pela linha F (x) = 5x +1
A: [todos os números reais]
Observa-se que para cada valor de domínio há uma imagem no codomain. Essa imagem é única, o que faz de F uma função injetiva . Do mesmo modo, observamos que o codomain da função é igual ao seu alcance. Assim cumprir a condição surjectivity .
Sendo injetivos e superjetivos ao mesmo tempo, podemos concluir que
F: R → R definido pela linha F (x) = 5x +1 é uma função bijetiva.
Isso se aplica a todas as funções lineares (funções cujo maior grau de variável é um).
Exercício 2
Seja a função F: R → R definida por F (x) = 3x 2 – 2
Ao desenhar uma linha horizontal, observa-se que o gráfico é encontrado em mais de uma ocasião. Por esse motivo, a função F não é injetiva e, portanto, não será bijetiva , desde que definida em R → R
Da mesma forma, existem valores de codomain que não são imagens de nenhum elemento do domínio. Por esse motivo, a função não é superjetiva, o que também merece condicionar o conjunto de chegadas.
O domínio e o co-domínio da função são condicionados
F: [0, ∞] → [- 2, ∞ ]
Onde se observa que o novo domínio abrange valores de zero ao infinito positivo. Evitando a repetição de valores que afetam a injetividade.
Assim também o codomain foi modificado, contando de “-2” ao infinito positivo, eliminando do codomain os valores que não correspondiam a nenhum elemento do domínio
Dessa maneira, pode-se garantir que F : [0, ∞] → [- 2, ∞ ] definido por F (x) = 3x 2 – 2
É bijetivo
Exercício 3
Seja a função F: R → R definida por F (x) = Sen (x)
No intervalo [- ∞ , + ∞ ] a função seno varia seus resultados entre zero e um.
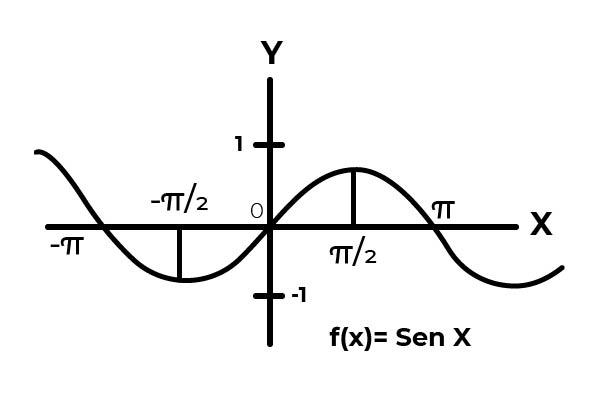
A função F não corresponde aos critérios de injetividade e super atividade, porque os valores da variável dependente são repetidos a cada intervalo de π. Além disso, os termos do codomain fora do intervalo [-1, 1] não são imagens de nenhum elemento do domínio.
Ao estudar o gráfico da função F (x) = Sen (x) , são observados intervalos em que o comportamento da curva atende aos critérios de bijetividade . Por exemplo, o intervalo D f = [ π / 2 , 3π / 2 ] para o domínio. Y C f = [-1, 1] para o codomain.
Onde a função varia os resultados de 1 a -1, sem repetir nenhum valor na variável dependente. E ao mesmo tempo o codomain é igual aos valores adotados pela expressão Sen (x)
Dessa forma, a função F: [ π / 2 , 3π / 2 ] → [-1, 1] definida por F (x) = Sen (x). É bijetivo
Exercício 4
Coloque as condições necessárias para D f e C f . Para que a expressão
F (x) = -x 2 é bijetivo.
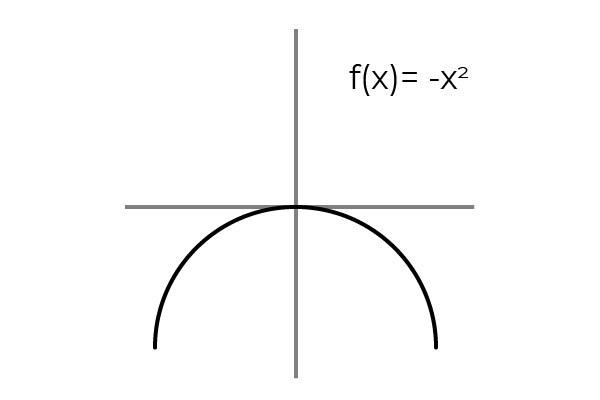
A repetição dos resultados é observada quando a variável assume valores opostos:
F (2) = F (-2) = -4
F (3) = F (-3) = -9
F (4) = F (-4) = -16
O domínio é condicionado, limitando-o ao lado direito da linha real.
D f = [0, + ∞ ]
Da mesma forma, observa-se que o intervalo dessa função é o intervalo [- ∞ , 0] , que, ao atuar como um co-domínio, atende às condições de super atividade.
Desta forma, podemos concluir que
A expressão F: [0, + ∞ ] → [- ∞ , 0] definida por F (x) = -x 2 É bijetivo
Exercícios propostos
Verifique se as seguintes funções são binárias:
F: [0, ∞) → R definido por F (x) = 3 (x + 1) 2 +2
F: [ 3π / 2 , 5π / 2 ] → R definido por F (x) = 5ctg (x)
F: [- π , π ] → R definido por F (x) = Cos (x – 3)
F: R → R definido pela linha F (x) = -5x + 4
Referências
- Introdução ao pensamento lógico e crítico. Merrilee H. Salmon. Universidade de Pittsburgh
- Problemas em Análise Matemática. Piotr Biler, Alfred Witkowski. Universidade de Wroclaw. Polônia
- Elementos de análise abstrata. Médico O’Searcoid PhD. Departamento de Matemática. Faculdade universitária de Dublin, Beldfield, Dublind 4
- Introdução à Lógica e à Metodologia das Ciências Dedutivas. Alfred Tarski, Nova Iorque, Oxford. Imprensa da Universidade de Oxford.
- Princípios de análise matemática. Enrique Linés Escardó. Editorial Reverté S. A 1991. Barcelona Espanha.