Como saber se duas frações são equivalentes usando tiras de fração

Início » Ciência » Matemática » Como saber se duas frações são equivalentes usando tiras de fração

Ao estudar frações na escola ou ajudar alguém com tarefas de matemática, uma dúvida que aparece sempre é: como identificar rapidamente quando duas frações representam a mesma quantidade? Com tiras de fração, a visualização fica muito mais clara, e com alguns testes simples a confirmação é certeira. Este guia completo completa a visão geométrica com explicações práticas de simplificação, multiplicação cruzada e geração de novas frações equivalentes.

Antes de mergulhar nas tiras, vale alinhar alguns conceitos fundamentais. Fração é uma forma de expressar partes de um todo, e quando dizemos que duas frações são equivalentes estamos afirmando que elas têm o mesmo valor, mesmo que “pareçam” diferentes. Você verá que 1/2, 2/4, 3/6 e 5/10 são, na prática, representações do mesmo número racional, pois todas descrevem a mesma porção do inteiro.

O que é fração e como ela se organiza

Fração é escrita como a/b. O número de cima é o numerador e o de baixo é o denominador. O numerador conta quantas partes iguais estão sendo consideradas, enquanto o denominador indica em quantas partes iguais o inteiro foi dividido.

Se uma pizza for cortada em 8 pedaços e você pegar 1 fatia, tem 1/8. Se juntar todas as 8 partes, volta ao inteiro. Esse mesmo raciocínio vale para qualquer contexto: tortas, barras de chocolate, segmentos de uma régua ou tiras de papel coloridas.

Outro detalhe útil: as frações pertencem ao conjunto dos números racionais, aqueles que podem ser escritos como quociente de dois inteiros com denominador diferente de zero. Dizer que duas frações são equivalentes é, essencialmente, afirmar que são iguais como números racionais.

Frações equivalentes com tiras de fração: visual e certeiro

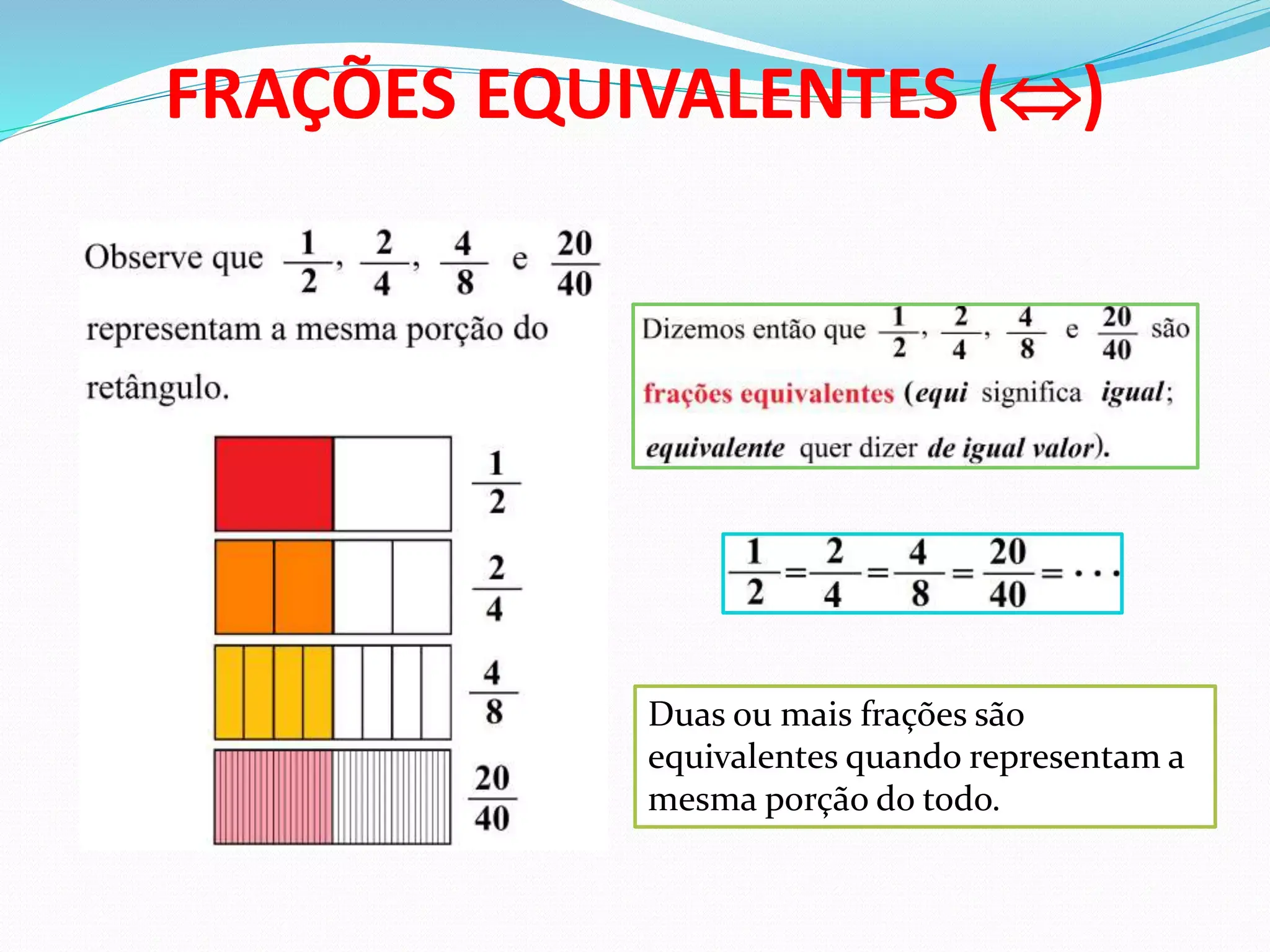
As tiras de fração são retângulos do mesmo comprimento, divididos em quantidades iguais de partes. Há tiras para metades, terços, quartos, quintos, sextos, oitavos e assim por diante. Para verificar se duas frações são equivalentes com tiras, basta alinhar as tiras correspondentes e comparar o comprimento coberto.

Por exemplo, compare 1/2 e 2/4. Pegue uma tira “meio” e outra “quartos”, selecione 2 em 4 partes na tira de quartos e veja se o comprimento ocupado é o mesmo da tira de 1/2. Se a extensão preenchida for igual, as frações são equivalentes; se houver sobra ou falta, elas não representam a mesma quantidade.

Isso funciona para muitos pares: 3/6, 4/8, 5/10 e 1/2 vão cobrir o mesmo comprimento nas tiras respectivas. As tiras traduzem o conceito em imagem e ajudam a evitar confusões comuns quando os números crescem.

Na prática de sala de aula, as tiras também são ótimas para comparar frações de denominadores diferentes, como 3/5 e 4/6; para ver equivalentes específicos, consulte frações equivalentes a 3/5. Se ao alinhar as tiras a cobertura não coincidir exatamente, elas não são equivalentes; ainda assim, dá para ver qual é maior de forma imediata.

O teste algébrico: multiplicação cruzada

Além do método visual, há um teste numérico rápido e infalível. Dadas duas frações a/b e c/d (com b e d não nulos), calcule a × d e b × c. Se os produtos cruzados forem iguais, então as frações são equivalentes.

Exemplo: 18/24 e 3/4. Multiplique em cruz: 18 × 4 = 72 e 24 × 3 = 72. Como os resultados coincidem, as frações são equivalentes. Esse teste também confirma que 6/24 equivale a 1/4, pois 6 × 4 = 24 e 24 × 1 = 24.

Outro caso clássico: 1/2 e 5/10. Em cruz, 1 × 10 = 10 e 2 × 5 = 10. Igualdade confirmada, equivalência garantida.

Como gerar frações equivalentes

Há uma regra simples para criar frações equivalentes: multiplique ou divida numerador e denominador por um mesmo número diferente de zero. Aplicando a mesma operação nos dois termos, o valor global do número racional não se altera.

Partindo de 1/5, multiplicando ambos os termos por 2, 3 e 5, obtemos 2/10, 3/15 e 5/25. Todas representam a mesma quantidade que 1/5, ainda que a escrita mude.

Com 4/3, multiplicando por 2, 3 e 4, surgem 8/6, 12/9 e 16/12. Essas escritas são úteis quando você precisa igualar denominadores para somar, subtrair ou comparar frações.

Dividir ambos os termos por um divisor comum é a chamada simplificação. 12/24, por exemplo, pode ser dividido por 12, resultando em 1/2. Se não houver mais divisor comum (além de 1), a fração está na forma irredutível.

Frações equivalentes: exemplos visuais e numéricos

Veja um conjunto clássico: 1/2, 2/4, 3/6, 4/8 e 5/10. Em qualquer diagrama de tiras ou em uma pizza, essas porções cobrem o mesmo espaço. No papel, basta simplificar cada uma até chegar a 1/2 para confirmar a equivalência.

Outro bloco conhecido: 5/8, 15/24 e 45/72. Multiplicando 5/8 por 3, obtemos 15/24; repetindo por 3, alcançamos 45/72. Se simplificarmos 45/72 dividindo por 9, caímos em 5/8, fechando o ciclo.

Para denominadores de 24, é fácil notar que 6/24 corresponde a 1/4; 12/24 equivale a 1/2; 18/24 equivale a 3/4. Você pode verificar com multiplicação cruzada ou simplificação direta dividindo por 6, 12 e 6, respectivamente.

Irredutível x redutível e a relação com decimais

Uma fração é redutível quando numerador e denominador têm um divisor comum maior que 1; é irredutível quando não há como continuar simplificando. Por exemplo, 5/8 é irredutível, mas 15/24 é redutível (divisor comum 3).

Algumas frações irredutíveis admitem representação decimal exata, como 1/2 = 0,5 e 5/8 = 0,625. Outras geram decimais periódicos, como 1/3 = 0,333… Se duas frações resultam no mesmo decimal, elas também são equivalentes.

Como usar as tiras de fração passo a passo

Para explorar equivalências com tiras, reúna as de mesmo comprimento (meio, terços, quartos, quintos etc.). Alinhe a borda esquerda de todas num mesmo ponto de partida para comparar coberturas.

Escolha duas frações, por exemplo, 2/4 e 3/6. Na tira de quartos, cubra 2 partes; na tira de sextos, cubra 3 partes. Observe se as extremidades à direita coincidem; se baterem no mesmo ponto, as frações são equivalentes.

Para exercícios, amplie a variedade: compare 4/12 com 1/3; compare 8/12 com 2/3; compare 9/12 com 3/4. Nas três situações, a equivalência é confirmada porque as coberturas são iguais na régua visual.

Comparar frações não equivalentes

Nem sempre as frações combinam. 3/5 e 4/6 são um bom teste. Com tiras, a extensão de 3/5 é levemente maior que a de 4/6? Vamos checar. Normalizando pelo mínimo múltiplo comum (MMC) de 5 e 6, que é 30, obtemos 18/30 e 20/30.

Concluímos que 4/6 = 2/3 = 20/30 é maior que 3/5 = 18/30. Logo, não são equivalentes, e a tira de sextos cobrirá uma faixa um pouco mais comprida.

Multiplicação cruzada: quando aplicar e por quê

O teste cruzado é ideal quando o visual não está à mão ou quando os números são grandes. Se a/b e c/d são frações quaisquer, compare a × d e b × c. Se a × d = b × c, as frações são equivalentes; se diferirem, não são.

Com 3/4 e 18/24: 3 × 24 = 72 e 4 × 18 = 72. Os produtos batem, então as frações são equivalentes.

Com 5/7 e 20/35: 5 × 35 = 175 e 7 × 20 = 140. Não batem? Repare que aqui há um erro proposital, pois 20/35 simplifica por 5 a 4/7, não a 5/7. Na verdade, o correto seria comparar 5/7 com 25/35: 5 × 35 = 175 e 7 × 25 = 175, e aí sim há equivalência.

Redução ao mesmo denominador

Outra forma de checar equivalência é reduzir frações diferentes ao mesmo denominador. Se, após a redução, os numeradores forem iguais, as frações são equivalentes. O uso do MMC ajuda a encontrar rapidamente um denominador comum conveniente.

Por exemplo, 3/5 e 12/20: o denominador comum 20 coloca a primeira fração em 12/20; a segunda já está assim. Como numeradores e denominadores coincidem, tratam-se de frações equivalentes.

Exemplos detalhados e passo a passo

Exemplo 1 — Equivalência direta: verifique se 6/24 e 1/4 são equivalentes. Simplificando 6/24 por 6, obtemos 1/4. Logo, são equivalentes.

Exemplo 2 — Equivalência via produto cruzado: 18/24 e 3/4. Calcule 18 × 4 = 72 e 24 × 3 = 72. Como os produtos batem, também são equivalentes.

Exemplo 3 — Geração de equivalentes: encontre três frações equivalentes a 1/5. Multiplicando por 2, 3 e 5, surgem 2/10, 3/15 e 5/25. Todas têm o mesmo valor que 1/5.

Exemplo 4 — Simplificação até a forma irredutível: simplifique 45/72. Divida por 9 e obtenha 5/8. Como 5 e 8 não têm divisor comum maior que 1, 5/8 é irredutível.

Exemplo 5 — Conversão decimal: 5/8 = 0,625. Duas frações que produzem o mesmo decimal são equivalentes.

Problemas resolvidos

Problema A — Verifique se 2/3 e 8/12 são frações equivalentes. Simplificando 8/12 por 4, obtemos 2/3. Portanto, tratam-se de frações equivalentes.

Problema B — Encontre x em x/224 = 3/7. Multiplique cruzado: 7x = 224 × 3 = 672, logo x = 672/7 = 96. Assim, a fração equivalente é 96/224.

Problema C — Qual fração não é equivalente a 13/8? Considere 65/40, 117/72, 52/32, 104/64 e 26/24. Simplificando, 65/40 ÷5 = 13/8; 117/72 ÷9 = 13/8; 52/32 ÷4 = 13/8; 104/64 ÷8 = 13/8; 26/24 ÷2 = 13/12. Logo, 26/24 não é equivalente a 13/8.

Problema D — Quem comeu mais pizza? Ana comeu 3/5 da pizza, Vitória comeu 4/6. Reduzindo ao mesmo denominador (30), temos 18/30 e 20/30. Como 20/30 > 18/30, Vitória comeu mais.

Dicas práticas para não errar

• Use tiras de fração para uma checagem visual rápida de equivalências.
• Simplifique sempre que possível; trabalhar com frações menores evita deslizes de cálculo.
• Multiplicação cruzada confirma equivalência em segundos quando os números crescem.
• Multiplique ou divida numerador e denominador pelo mesmo número para gerar equivalentes.

Mais exemplos para treinar

a) Mostre que 9/12 é equivalente a 3/4. Divida por 3: 9/12 → 3/4. Confirmado.

b) Verifique se 7/21 e 1/3 são equivalentes. Divida por 7: 7/21 → 1/3. Equivalência verdadeira.

c) Encontre dois equivalentes para 4/9. Multiplicando por 2 e 3: 8/18 e 12/27. Ambos mantêm o mesmo valor.

d) Compare 5/10 e 2/5. Simplifique 5/10 para 1/2 e veja que 1/2 não é 2/5. Em cruz: 5 × 5 = 25, 10 × 2 = 20. Como 25 ≠ 20, não são equivalentes.

Frações equivalentes no cotidiano

Frações equivalentes aparecem naturalmente: em receitas (metade de uma xícara é o mesmo que dois quartos), em medidas (25/100 de um metro é 1/4 de metro) e em finanças (50% é 1/2). Dominar o conceito facilita conversões, estimativas e comparações rápidas.

No ensino, alternar entre tiras, simplificações e produtos cruzados consolida o entendimento. O visual ajuda na intuição, e os testes numéricos garantem precisão.

Conexões com operações entre frações

Para somar e subtrair, muitas vezes é preciso reescrever frações equivalentes com denominadores iguais. Esse “ajuste” preserva o valor e habilita a operação.

Na multiplicação, não é necessário igualar denominadores, mas simplificar fatores comuns antes de multiplicar reduz esforço. Na divisão, multiplicar pela fração inversa também se beneficia de simplificações prévias.

Erros comuns e como evitá-los

Erro 1: multiplicar apenas o numerador (ou só o denominador) ao gerar equivalentes. Sempre multiplique ou divida ambos os termos pelo mesmo número.

Erro 2: esquecer de simplificar ao final. Uma resposta correta pode ser aceita, mas a forma irredutível é a padrão. Ela facilita comparações e validações.

Erro 3: confundir aproximação decimal com equivalência. 0,33 não é exatamente 1/3, e sim uma aproximação. Use produtos cruzados para confirmar igualdade exata.

Pequeno roteiro para checagem rápida

1) Se tiver tiras de fração, alinhe e compare a extensão coberta. Coincidiu? Geralmente é equivalência.

2) Se não tiver material visual, simplifique ambas as frações. Se chegarem à mesma forma irredutível, são equivalentes.

3) Em dúvida, multiplique cruzado a/b e c/d. Se a × d = b × c, equivalência confirmada.

Prática extra com números maiores

Teste 1: 28/42 e 2/3. Simplifique 28/42 por 14 e obtenha 2/3. Equivalente.

Teste 2: 14/35 e 2/5. Divida por 7: 14/35 → 2/5. Equivalente.

Teste 3: 21/49 e 3/7. Divida por 7: 21/49 → 3/7. Equivalente.

Teste 4: 16/24 e 2/3. Divida 16/24 por 8 e obtenha 2/3. Equivalente.

Teste 5: 18/24 e 2/3. Simplifique 18/24 por 6 → 3/4; como 3/4 ≠ 2/3, não são equivalentes.

Aplicando o conceito em comparações

Quando você precisa decidir qual fração é maior, escolha entre tiras, decimais ou denominadores comuns. Frações equivalentes são uma ponte: transformam a escrita sem mudar o valor, facilitando comparações justas; veja um exemplo de comparação para aprofundar.

Ex.: 7/10 e 3/4. Com denominador 20, obtemos 14/20 e 15/20. Logo, 3/4 é maior; fica claro quando as frações “falam a mesma língua”.

A ideia central fica cristalina: duas frações são equivalentes quando representam a mesma porção do inteiro, e isso pode ser visto nas tiras de fração, confirmado pela simplificação e garantido pela multiplicação cruzada. Com esse tripé — visual, algébrico e prático — você identifica equivalências com segurança em qualquer contexto, do cotidiano às avaliações mais exigentes.