- Frações representam partes de um todo e podem ser entendidas como resultado de divisões em partes iguais, ligando numerador, denominador e situações reais.
- Representações gráficas em figuras e na reta numérica tornam visíveis conceitos como tipos de frações, equivalência, comparação e operações básicas.
- Frações equivalentes e simplificação permitem escrever a mesma quantidade de formas diferentes, facilitando cálculos e a compreensão de classes de equivalência.
- Atividades práticas com materiais concretos e problemas contextualizados são essenciais para desenvolver as habilidades previstas na BNCC ligadas às frações.

Entender como representar frações graficamente é uma das chaves para perder o medo da matemática e conseguir explicar esse conteúdo com clareza para crianças e adolescentes. Quando o aluno vê a fração só como dois números separados por um traço, tudo parece muito abstrato; mas, a partir do momento em que enxerga pedaços de pizza, barras coloridas, retângulos divididos ou pontos na reta numérica, o conceito começa a fazer sentido de verdade.
Neste artigo, vamos juntar a visão da didática escolar com o rigor matemático para mostrar, em detalhes, o que são frações, como ler e classificar cada tipo, como representá-las visualmente (em figuras e na reta numérica) e como trabalhar com operações e atividades práticas em sala de aula. Tudo em linguagem acessível, mas sem perder a profundidade, para que você possa estudar, revisar ou ensinar frações com segurança.
O que é uma fração e como ela surge no dia a dia
Uma fração é um número racional que indica partes de um inteiro ou o resultado de uma divisão entre dois números inteiros. Sempre que você divide algo em partes iguais e pega algumas dessas partes, está trabalhando com frações: um pedaço de bolo, um terço do salário, três quartos de um terreno, e assim por diante.
A notação padrão de uma fração é a/b, em que o número de cima (a) é o numerador e o número de baixo (b) é o denominador. O numerador mostra quantas partes estão sendo consideradas e o denominador mostra em quantas partes iguais o todo foi dividido. Assim, em 3/4, temos 3 partes consideradas de um total de 4 partes iguais.
Historicamente, o uso de frações nasceu de necessidades bem concretas, como a medição de terras no Egito antigo. Ao usar cordas para medir terrenos, as pessoas percebiam que nem sempre cabia um número inteiro de unidades de medida no lado do terreno; então, passaram a considerar pedaços dessa unidade, criando, na prática, os números fracionários.
No conjunto dos números, as frações fazem parte dos números racionais não negativos (Q+), que incluem tanto os inteiros (0, 1, 2, 3, …) quanto as frações positivas (1/2, 3/4, 5/6, …). Ao representar esses números com frações, conseguimos descrever situações em que não estamos lidando com quantidades inteiras, mas com porções.
Uma interpretação muito útil em sala de aula é sempre associar fração a “partes iguais de um todo”: dividir uma barra de chocolate em 4 pedaços do mesmo tamanho, repartir dinheiro entre filhos de forma igualitária, distribuir frutas igualmente em cestas ou marcar distâncias em uma régua ou em uma fita métrica.
Numerador, denominador e leitura correta das frações
Os dois termos de uma fração têm significados bem definidos. O numerador representa quantas partes estamos tomando e o denominador indica em quantas partes o inteiro foi dividido. Em linguagem de divisão, o numerador funciona como dividendo e o denominador como divisor, sempre lembrando que o denominador não pode ser zero.
A leitura da fração depende principalmente do denominador. O numerador é lido normalmente em forma cardinal (um, dois, três, quatro…), e o denominador é lido em forma fracionária (meio, terço, quarto, quinto, etc.). Assim, 1/2 é lido “um meio”, 3/4 é lido “três quartos” e 5/8 é lido “cinco oitavos”.
Para denominadores entre 2 e 9, usamos nomes específicos: meio (1/2), terço (1/3), quarto (1/4), quinto (1/5), sexto (1/6), sétimo (1/7), oitavo (1/8) e nono (1/9). Quando o denominador é maior que 10 e não é múltiplo de 10, é comum acrescentar a palavra “avos”: por exemplo, 1/11 é “um onze avos”, 1/17 é “um dezessete avos”.
Quando o denominador é múltiplo de 10, temos também nomes específicos muito usados em contexto de medidas e porcentagens: 1/10 é “um décimo”, 1/100 é “um centésimo”, 1/1000 é “um milésimo”. Para denominadores como 1/20, 1/30 ou 1/40, podemos falar “um vinte avos (vigésimo)”, “um trinta avos (trigésimo)” e assim por diante.
No cotidiano escolar, é comum os alunos se confundirem, acreditando que frações com denominador maior representam pedaços maiores. É importante reforçar visualmente que, quanto maior o denominador, menor é cada parte: um pedaço de pizza cortada em 8 partes é menor do que um pedaço da mesma pizza cortada em 4 partes.
Principais tipos de frações e seus significados
As frações podem ser classificadas de acordo com a relação entre numerador e denominador e com o tipo de quantidade que representam. Trabalhar essa classificação com exemplos e desenhos ajuda a fixar o conceito e evita confusões mais à frente, especialmente ao comparar ou operar frações. Veja também o artigo sobre frações: tipos, exemplos e exercícios.
Fração própria é aquela em que o numerador é menor que o denominador, representando uma quantidade menor que 1 inteiro. Por exemplo, 1/2, 3/4 ou 12/100 são frações próprias: estamos pegando menos partes do que o total disponível. Visualmente, vemos apenas uma parte sombreada do todo.
Fração imprópria é a fração em que o numerador é maior que o denominador, como 9/8, 7/2 ou 25/12. Nesse caso, a quantidade representada é maior do que 1 inteiro, porque estamos tomando mais partes do que as que formam um único todo. Essa ideia é muito útil, por exemplo, ao trabalhar quantidades acumuladas em receitas ou medidas.
Fração aparente é uma fração que, na prática, representa um número inteiro, porque o numerador é múltiplo do denominador. Exemplos típicos são 2/2, 8/4 e 9/3: ao fazer a divisão, obtemos 1, 2 e 3, respectivamente. Frações como 0/3 ou 0/8 também são consideradas aparentes, pois o resultado é o número inteiro 0.
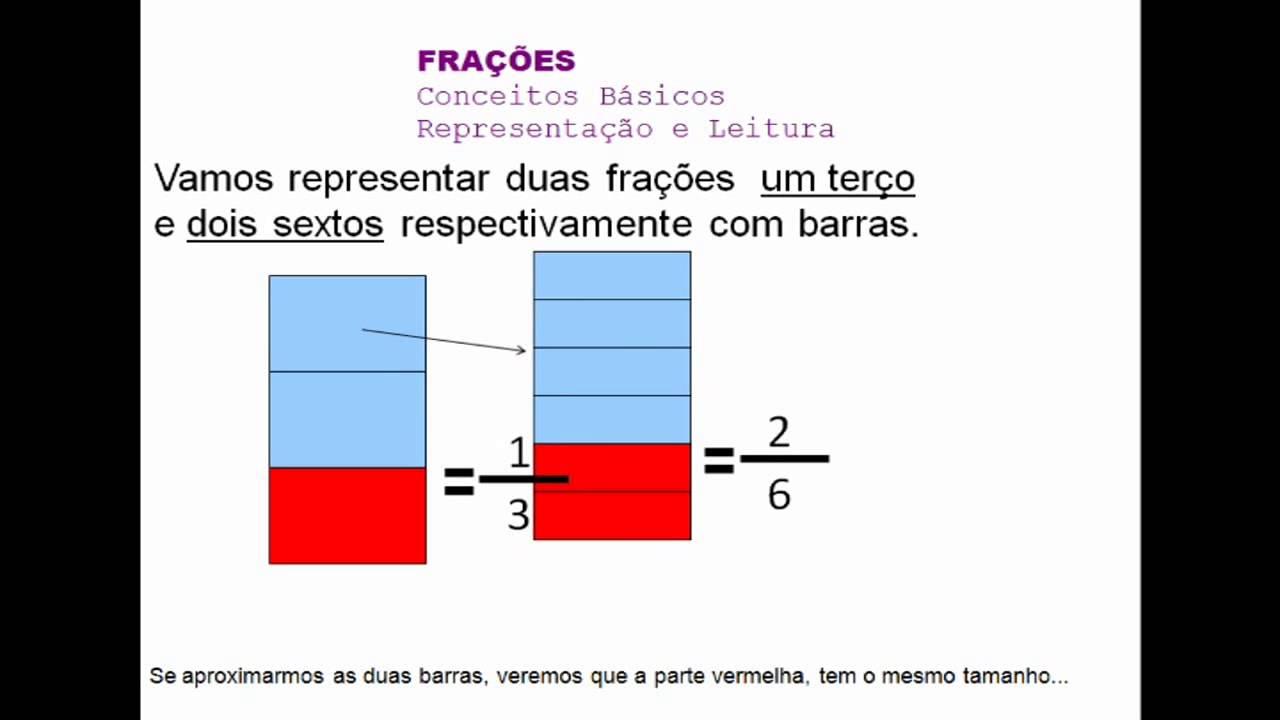
Frações equivalentes são diferentes maneiras de escrever a mesma quantidade fracionária. Se multiplicarmos numerador e denominador de 1/2 por 2, obtemos 2/4; multiplicando por 3, obtemos 3/6; por 4, obtemos 4/8. Todas essas representações correspondem à mesma parte do todo, como se vê claramente ao colorir a mesma porção em retângulos divididos em 2, 4, 6 ou 8 partes.
Fração irredutível é a forma mais simples de uma fração, aquela em que numerador e denominador não possuem nenhum divisor comum além de 1. Por exemplo, 12/15 pode ser simplificada dividindo ambos os termos por 3, resultando em 4/5. Nesse caso, 4/5 é irredutível, pois não existe outro número (diferente de 1) que divida simultaneamente 4 e 5.
Fração mista, ou número misto, é uma maneira de escrever, de forma mais intuitiva, frações impróprias, separando a parte inteira da parte fracionária. Assim, 3 4/9 significa 3 inteiros mais 4/9; 9 3/4 e 2 1/3 seguem a mesma lógica. Transformar frações impróprias em números mistos e vice-versa é um procedimento importante na resolução de problemas.
Representação gráfica de frações em figuras
A representação gráfica de frações transforma números em imagens, permitindo que o aluno literalmente enxergue o que o numerador e o denominador significam. Para isso, é comum usar figuras geométricas (retângulos, círculos, barras), objetos do cotidiano (pizza, chocolate, frutas), tabelas e diagramas.
Uma forma clássica é desenhar um retângulo ou um círculo e dividi-lo em partes iguais: duas, três, quatro, seis, oito… Em seguida, sombreamos tantas partes quanto indica o numerador. Se desenharmos um retângulo dividido em quatro colunas iguais e colorirmos três delas, teremos uma representação visual de 3/4: três partes marcadas de um total de quatro.
Para destacar frações equivalentes, podemos usar figuras com subdivisões diferentes que representem a mesma área colorida. Por exemplo, um retângulo inteiro colorido representa 1; um retângulo dividido em 2 partes com 1 parte colorida mostra 1/2; outro, dividido em 4 partes com 2 coloridas, representa 2/4; um terceiro, com 6 partes e 3 coloridas, representa 3/6; um quarto, com 8 partes, mostra 4/8. O aluno percebe que a área em destaque é a mesma, mesmo que a fração escrita mude.
Frações próprias e impróprias também podem ser mostradas em blocos. Em 3/4, desenhamos apenas um bloco (um inteiro) dividido em 4 partes, com 3 partes coloridas. Já em 5/4, precisamos de mais de um inteiro: desenhamos um primeiro retângulo dividido em 4, com as 4 partes coloridas, e um segundo retângulo com apenas 1 parte (de 4) colorida. Assim, o estudante vê que 5/4 é maior do que 1 inteiro.
Frações aparentes se tornam claras pela representação em blocos completos. Se representarmos 8/4 em um retângulo dividido em 4 partes e outro retângulo também dividido em 4 partes, com todas as partes coloridas, veremos dois inteiros. A fração “parece” uma fração, mas o desenho revela que o valor é um número inteiro, no caso, 2.
Em atividades impressas, é muito comum usar barras ou conjuntos de objetos: por exemplo, 35 moedas distribuídas em 7 grupos iguais para trabalhar sétimos (1/7, 2/7, 3/7…), uma herança dividida em 3 partes iguais para trabalhar terços (1/3, 2/3, 3/3) e frutas organizadas em 4 cestas iguais para trabalhar quartos (1/4, 2/4, 3/4, 4/4 e até 5/4).
Representação de frações na reta numérica
A reta numérica é outro recurso gráfico essencial para representar frações, pois ajuda o aluno a entender que frações são números que ocupam posições específicas entre os inteiros. Isso é importante para desenvolver a noção de ordem, comparação e distância entre números racionais.
Para marcar uma fração unitária usual, como 1/2, 1/3 ou 1/4, dividimos o segmento de 0 a 1 em partes iguais de acordo com o denominador. Em seguida, marcamos o ponto correspondente ao numerador. Assim, 1/2 fica exatamente no meio entre 0 e 1; 1/4 fica na primeira marca de quatro divisões iguais; 3/4 fica na terceira marca, e assim por diante.
Essa mesma lógica vale para frações maiores que 1. Para representar 5/4 na reta, podemos pensar que 4/4 coincide com o número 1. Então, 5/4 fica um “quarto” além de 1. Na prática, dividimos o intervalo entre 0 e 2 em 8 partes iguais (ou dividimos de 0 a 1 em 4 e repetimos o padrão entre 1 e 2) e marcamos 5 dessas partes.
As habilidades da BNCC (como EF04MA09 e EF05MA02) enfatizam exatamente essa conexão entre frações, medidas e reta numérica: reconhecer frações unitárias como medidas menores que a unidade, compreender a escrita decimal de alguns racionais e perceber que toda fração pode ser associada a um ponto na reta.
Ao trabalhar graficamente, é interessante alternar representações em figuras e na reta, mostrando ao aluno que 1/2 pode ser metade de uma figura colorida e, ao mesmo tempo, um ponto bem definido no meio do caminho de 0 a 1. Essa ponte entre o concreto (imagens) e o abstrato (números na reta) é crucial para consolidar o conceito de fração.
Frações no contexto de divisão em partes iguais
Uma das interpretações mais intuitivas de frações é como resultado de uma divisão em partes iguais. Imagine dividir um salário, uma herança, moedas, frutas ou brinquedos; sempre que todos devem receber partes idênticas, estamos traduzindo a conta de divisão em linguagem de fração.
Exemplo com moedas: se Josué tem 35 moedas e resolve dividi-las em 7 conjuntos idênticos, cada grupo terá 5 moedas. A fração 1/7 de 35 corresponde a 5 moedas, 2/7 de 35 correspondem a 10 moedas, 3/7 correspondem a 15 moedas, e assim por diante. Em uma atividade gráfica, podemos representar cada grupo de 5 moedas como 1/7 do total.
Exemplo com herança: uma herança de R$ 1.650,00 distribuída igualmente para 3 filhos significa que cada um recebe 1/3 desse valor. Representando graficamente, podemos mostrar três blocos idênticos, cada um indicando o valor de um terço. Se somarmos as três partes (3/3), voltamos ao valor total de R$ 1.650,00, reforçando a ideia de que a soma das partes forma o inteiro.
Exemplo com frutas: Edir divide 32 frutas igualmente em 4 cestas, de modo que cada cesta fica com 8 frutas. Aqui, 1/4 de 32 são 8 frutas. Podemos trabalhar 2/4 (16 frutas), 3/4 (24 frutas), 4/4 (32 frutas) e até 5/4 de 32 (que já é maior do que o total de uma distribuição simples), introduzindo assim, de forma visual, a ideia de frações impróprias.
Nessas atividades, o aluno percebe que frações são, ao mesmo tempo, divisão e quantidade: 1/4 de 32 é o resultado de dividir 32 por 4; mas também é uma quantidade concreta de 8 frutas, que pode ser desenhada, contada e manipulada. Isso torna o conteúdo muito menos ameaçador e mais significativo.
Frações equivalentes, simplificação e classe de equivalência
Frações equivalentes aparecem naturalmente quando representamos a mesma área com subdivisões diferentes. Se desenhamos um retângulo inteiro e o chamamos de 1, e depois o dividimos em 2, 4, 6 e 8 partes, podemos colorir metade do retângulo em todos os casos. Mesmo que escrevamos 1/2, 2/4, 3/6 ou 4/8, a porção destacada é a mesma.
Algebricamente, obtemos frações equivalentes multiplicando ou dividindo numerador e denominador pelo mesmo número natural diferente de zero. Por exemplo, 1/2 pode ser transformado em 2/4 multiplicando ambos por 2, em 3/6 multiplicando por 3, e assim por diante. Já 12/16 pode ser simplificado sucessivamente: 12/16 ÷ 2 = 6/8, e 6/8 ÷ 2 = 3/4, que é irredutível.
O conjunto de todas as frações equivalentes a uma fração dada é chamado de classe de equivalência. Por exemplo, a classe de equivalência de 1/3 inclui 1/3, 2/6, 3/9, 4/12, 5/15, 6/18, etc. Em teoria dos números, escolhemos uma única representante dessa classe, geralmente a forma irredutível, para trabalhar de maneira mais simples.
Simplificar uma fração significa justamente encontrar essa forma irredutível. Podemos fazer isso por divisões sucessivas: dividir numerador e denominador por fatores comuns até que não seja mais possível. Outro caminho é encontrar diretamente o Máximo Divisor Comum (MDC) entre os dois números e dividir ambos por esse valor, chegando rapidamente à fração mais simples.
Por exemplo, ao simplificar 36/60, dividimos sucessivamente por 2, obtendo 18/30, depois 9/15, e finalmente dividimos por 3, chegando a 3/5. Já em 54/72, sabemos que o MDC(54,72) é 18; então, basta fazer 54÷18 e 72÷18 para obter diretamente 3/4. Em atividades com representação gráfica, a simplificação corresponde a substituir uma figura muito “picada” por outra, com menos divisões, mas com a mesma área colorida.
Comparação de frações com apoio visual e algébrico
Comparar frações é muito mais fácil quando usamos representações gráficas, sobretudo nas séries iniciais, em que o cálculo de MMC ainda pode ser difícil para as crianças. Ao desenhar retângulos, pizzas ou barras fracionárias, o aluno consegue ver qual área é maior.
Se as frações têm o mesmo denominador, a regra é simples: a fração com maior numerador é a maior, pois estamos comparando quantidades de partes do mesmo tamanho. Por exemplo, entre 3/5 e 4/5, 4/5 é claramente maior. Em um desenho, colorimos 3 partes em um retângulo e 4 partes em outro, ambos divididos em 5 partes iguais; visualmente, a segunda área é maior.
Se os denominadores são diferentes, podemos recorrer à redução ao mesmo denominador. Usamos o Mínimo Múltiplo Comum (MMC) dos denominadores para construir frações equivalentes com o mesmo denominador. Por exemplo, ao comparar 2/3 e 3/5, calculamos MMC(3,5)=15 e transformamos 2/3 em 10/15 e 3/5 em 9/15. Como 10/15 é maior que 9/15, concluímos que 2/3 > 3/5.
Quando os numeradores são iguais, vale uma observação curiosa: a fração com denominador menor é a maior, pois cada parte é maior. Em 3/4 e 3/8, ambos têm 3 partes, mas os quartos são maiores que os oitavos. Representando em figuras, colorimos 3 de 4 partes em um retângulo e 3 de 8 em outro; a área marcada em vermelho será maior na primeira figura, mostrando que 3/4 > 3/8.
A reta numérica também ajuda na comparação. Ao marcar 3/4 e 3/8 na reta, dividindo o trecho entre 0 e 1 em 8 partes, notamos que 3/4 coincide com 6/8, portanto o ponto de 3/4 (ou 6/8) fica mais à direita do que o ponto de 3/8. Assim, visual e numericamente, confirmamos a desigualdade.
Operações com frações e interpretação visual
As quatro operações básicas com frações (adição, subtração, multiplicação e divisão) podem e devem ser acompanhadas de representações gráficas, especialmente nas etapas iniciais de aprendizagem. Isso ajuda a dar sentido aos procedimentos algébricos, que, sozinhos, costumam parecer “regras decoradas”.
Na adição e subtração de frações com mesmo denominador, conservamos o denominador e somamos ou subtraímos apenas os numeradores. Por exemplo, 3/5 + 1/5 = 4/5 e 5/7 − 3/7 = 2/7. Em termos visuais, é como juntar ou retirar partes de um mesmo tipo de pedaço: juntamos 3 pedaços de 1/5 com mais 1 pedaço de 1/5, totalizando 4 pedaços de 1/5.
Quando os denominadores são diferentes, precisamos torná-los iguais encontrando frações equivalentes. Pegando 1/6 + 3/4 como exemplo, calculamos o MMC(6,4)=12. Transformamos 1/6 em 2/12 (multiplicando numerador e denominador por 2) e 3/4 em 9/12 (multiplicando por 3). Com denominadores iguais, somamos 2/12 + 9/12 = 11/12. Em uma figura de 12 partes, teríamos 11 partes coloridas.
Na multiplicação de frações, a regra é objetiva: multiplicamos numerador por numerador e denominador por denominador. Se fizermos 3/5 × 4/7, obtemos 12/35. Visualmente, essa operação pode ser entendida como “parte de parte”: 3/5 de um inteiro, e depois 4/7 dessa quantidade, o que leva à construção de retângulos divididos nos dois sentidos, resultando em um total de 35 pequenas partes, das quais 12 ficam destacadas.
A divisão de frações é frequentemente a operação que mais causa dúvidas. Uma forma didática de explicá-la é pensar: “quantas vezes a segunda fração cabe na primeira?”. Se tomamos 1/2 ÷ 2/3, podemos primeiro reescrever essas frações com o mesmo denominador: 1/2 = 3/6 e 2/3 = 4/6. Em uma representação, 3/6 correspondem a 3 partes coloridas em 6, e 4/6 correspondem a 4 partes coloridas em 6. A pergunta passa a ser: em cada conjunto de 4 partes, quantas delas estão ocupadas por 3 partes? O resultado é 3/4.
Algebricamente, isso justifica a “regra do inverso”: dividir por uma fração equivale a multiplicar pela fração inversa. Assim, 1/2 ÷ 2/3 = 1/2 × 3/2 = 3/4. De forma geral, para a/b ÷ c/d, mantemos a/b e multiplicamos por d/c, ou seja, (a/b) × (d/c) = ad/bc. A visualização com retângulos divididos em sextos, como no exemplo, ajuda o aluno a enxergar que faz sentido “virar” a segunda fração.
Leitura, vocabulário e atividades de sala de aula
Além da parte numérica e gráfica, trabalhar o vocabulário de frações é fundamental. Termos como metade, terço, quarto, quinto, centésimo, milésimo, sétimo, oitavo e “avos” precisam ser compreendidos e usados com segurança. Isso ajuda tanto na interpretação de problemas quanto na comunicação em sala.
Atividades práticas com materiais concretos tornam o aprendizado mais significativo. Cortar folhas de papel em partes iguais, usar blocos coloridos, recortar figuras, dividir pizzas de papel ou até mesmo repartir alimentos reais (como bolos e barras de chocolate) são estratégias que ajudam o aluno a associar o símbolo fracionário à realidade.
Problemas contextualizados, como o da aluna que guarda 3/10 do salário e gasta 1/10 com aluguel, aproximam a fração da vida financeira cotidiana. Nesse caso, o salário está dividido em 10 partes iguais; se 3/10 vão para a poupança e 1/10 para o aluguel, foram usadas 4 partes. Sobram 6/10 do salário, o que pode ser representado graficamente em uma barra dividida em 10 segmentos, dos quais 6 permanecem livres.
Outra linha de atividades envolve explicar a leitura de frações menos usuais, como 1/3597, que pode ser lida “um, três mil quinhentos e noventa e sete avos”. Embora não sejam usadas no dia a dia, essas frações mostram que o conceito é geral e que o denominador pode ser qualquer número natural positivo.
Trabalhar com exercícios progressivos de reconhecimento, leitura, representação e operação desenvolve diversas habilidades previstas na Base Nacional Comum Curricular (BNCC), como relacionar números e quantidades, compreender partes de um todo, operar com racionais e transitar entre diferentes registros (numérico, verbal, gráfico, geométrico e na reta numérica).
Ao integrar representação gráfica, linguagem clara e problemas contextualizados, o tema das frações deixa de ser uma sequência de “regras decoradas” e passa a ser uma ferramenta útil para entender divisões justas, medidas, porcentagens, proporções e várias situações do cotidiano, fortalecendo de forma consistente o raciocínio matemático dos alunos.
