Como converter frações mistas em razões: método, exemplos e dicas

Início » Ciência » Matemática » Como converter frações mistas em razões: método, exemplos e dicas

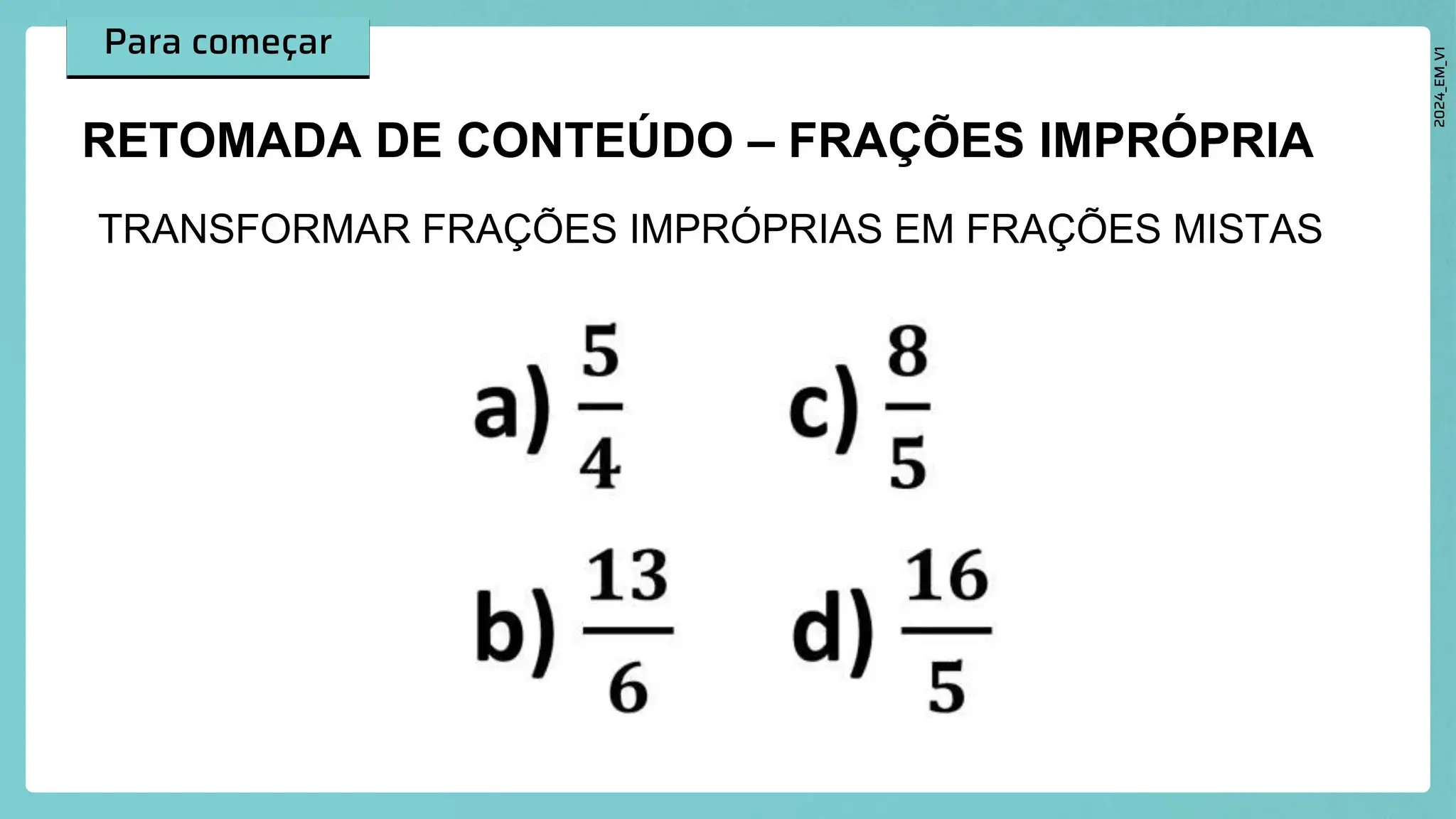
Entender como transformar uma fração mista em uma razão é uma habilidade matemática que aparece o tempo todo em problemas práticos e exercícios escolares. Ao dominar esse processo, você consegue comparar quantidades de forma direta, comunicar proporções com clareza e resolver questões que envolvem escalas, receitas, mapas e estatísticas. Apesar de parecer um tema simples, há detalhes importantes que fazem toda a diferença na hora de acertar sempre e evitar tropeços comuns.

Antes de colocar a mão na massa, vale alinhar a ideia central: uma fração mista é um número composto por uma parte inteira e uma parte fracionária (por exemplo, 2 1/3), enquanto uma razão é uma comparação entre duas grandezas, usualmente escrita no formato a:b. Converter de um para o outro exige uma sequência curta de passos, mas exige atenção com a simplificação, a ordem dos termos e o contexto de uso da razão (proporção, taxa ou comparação direta).

O que é uma fração mista e o que é uma razão

Por definição, fração mista é a combinação de um inteiro com uma fração própria, como 3 2/5, onde 3 é a parte inteira e 2/5 é a parte fracionária. Quando precisamos operá-la, quase sempre compensa reescrevê-la como fração imprópria, pois isso padroniza os cálculos e facilita conversões.

Já a razão representa a relação entre duas quantidades, escrita como a:b ou a/b. Em linguagem de proporções, 3:2 significa que, para cada 3 unidades de uma grandeza, há 2 unidades da outra. Essa escrita é onipresente em escalas de mapas, concentrações de soluções, receitas culinárias e estatísticas de esportes.

É crucial notar que a ordem dos termos na razão importa. A razão 3:2 não é a mesma que 2:3; inverter a ordem muda completamente a comparação entre as grandezas, o que pode levar a interpretações equivocadas nos enunciados.

Outro ponto de atenção: razão pode ou não envolver unidades. Se compararmos quantidades da mesma natureza (ex.: maçãs para peras), frequentemente omitimos unidades. Já em taxas (ex.: quilômetros por hora), a razão carrega unidades, embora a técnica de conversão a partir da fração mista permaneça a mesma.

Por que converter frações mistas em razões

Existem cenários em que expressar o resultado como razão é mais direto e comunicativo. Quando queremos apresentar proporções de mistura, escalas e comparações relativas, a notação a:b é mais intuitiva do que um número misto. Por exemplo, dizer 7:3 transmite imediatamente a composição relativa entre duas partes, sem ambiguidade.

Em problemas de receita, é comum que a lista de ingredientes traga frações mistas; convertê-las para razões deixa claro como redimensionar as quantidades mantendo a mesma proporção. O mesmo vale para mapas e desenhos técnicos em que a escala precisa ser aplicada uniformemente em todas as medidas.

Na comunicação de dados e estatísticas, razões facilitam a comparação lado a lado. Não por acaso, indicadores esportivos, proporções demográficas e índices de desempenho aparecem como razões simplificadas, pois são fáceis de ler, simplificar e comparar com outras razões equivalentes.

Passo a passo: da fração mista à razão

O caminho mais seguro para converter fração mista em razão passa por reescrever a fração mista como fração imprópria e, em seguida, ajustar para o formato a:b. Seguir uma rotina curta evita erros de distração e garante que a razão final esteja na forma mais clara e reduzida.

1. Transforme a fração mista em fração imprópria: se a fração mista é A B/C, calcule o numerador como A×C + B e mantenha o denominador C. Exemplo: 2 1/3 → (2×3 + 1)/3 = 7/3.
2. Escreva a razão: o numerador passa a ser o primeiro termo e o denominador, o segundo termo, formando a:b. Ex.: 7/3 → 7:3.
3. Simplifique a razão, se possível: divida ambos os termos pelo máximo divisor comum (MDC). Ex.: 12:8 → dividir por 4 → 3:2.
4. Cheque a ordem e o contexto: confirme se a ordem dos termos reflete a comparação pedida no problema. Às vezes a razão solicitada é “parte A para parte B”; invertê-la sem querer muda o significado.

Vamos a alguns exemplos diretos. Exemplo 1: 1 1/2 → 3/2 → 3:2 (já está simplificada). Exemplo 2: 4 2/5 → (4×5 + 2)/5 = 22/5 → 22:5 (não simplifica, pois 22 e 5 são coprimos). Exemplo 3: 3 3/6 → (3×6 + 3)/6 = 21/6 → 7:2 (dividimos ambos por 3).

Se preferir uma forma mental rápida: multiplique o inteiro pelo denominador, some o numerador e coloque tudo “sobre” o mesmo denominador; depois, transcreva como a:b. Esse automatismo reduz etapas escritas e ajuda na fluidez durante provas e exercícios cronometrados.

Exemplos práticos e verificação

Para ganhar confiança, observe uma coletânea de conversões típicas, com atenção à simplificação final. Ter um repertório de exemplos “na cabeça” acelera muito a resolução.

Fração mista	Fração imprópria	Razão (a:b)	Observações
2 1/3	7/3	7:3	Já está em forma reduzida
5 4/8	44/8	11:2	Divide por 4 para simplificar
1 3/4	7/4	7:4	Não simplifica (7 e 4 são coprimos)
3 2/3	11/3	11:3	Permanece 11:3
2 3/6	15/6	5:2	Divide por 3 após 15:6 → 5:2
4 1/5	21/5	21:5	Sem redução

Uma forma de validar mentalmente a conversão é reverter o processo. Se 7:3 é sua razão, reescreva como 7/3 e transforme a fração em mista: 7/3 = 2 1/3. Essa checagem de ida e volta confirma se não houve troca indevida de termos ou erro no cálculo do numerador impróprio.

Também é útil comparar razões equivalentes. 7:3 é equivalente a 14:6, 21:9, 28:12… Multiplicar ambos os termos por um mesmo fator mantém a proporção. Isso ajuda a identificar simplificações possíveis quando a conversão gera termos grandes que ainda possuem fatores comuns.

Simplificação eficiente com o MDC

Para reduzir a razão à forma mais simples, use o máximo divisor comum (MDC) entre os dois termos. A ideia é dividir ambos pelo maior número inteiro que os divide simultaneamente, garantindo a apresentação mais enxuta possível da proporção.

Você pode encontrar o MDC de diferentes formas, e vale escolher a que for mais confortável no momento. Alguns métodos são mais rápidos à mão, outros brilham com números maiores.

• Fatoração em primos: decomponha cada termo em fatores primos e multiplique os fatores comuns pelos menores expoentes. Bom para valores moderados.
• Algoritmo de Euclides: aplique divisões sucessivas até chegar ao resto 0; o último resto não nulo é o MDC. Excelente para números grandes.
• Inspeção por divisores comuns: teste divisores pequenos (2, 3, 5, 7…) quando os termos tiverem “cara” de múltiplos desses números.

Exemplo rápido: 44:8 → MDC(44, 8) = 4 → 11:2. Outro: 36:24 → MDC = 12 → 3:2. Essa etapa de simplificação é o “polimento” final na apresentação da razão convertida a partir da fração mista.

Casos especiais e armadilhas comuns

Frações mistas com numerador que permite simplificação imediata merecem atenção. Em 3 3/6, a parte fracionária 3/6 já se reduz a 1/2; você pode simplificar antes ou depois. Fazendo depois: (3×6 + 3)/6 = 21/6 → 7:2. Fazendo antes: 3 1/2 → (3×2 + 1)/2 = 7/2 → 7:2. O resultado coincide, e simplificar cedo às vezes diminui contas.

Quando há inteiros grandes, é fácil errar no produto A×C. Use parênteses e escreva a multiplicação completa para evitar confundir 4×7 + 5 com 4×(7+5). Pequenos deslizes no cálculo do numerador impróprio geram razões totalmente distintas na saída.

Negativos pedem cuidado extra. −2 1/4 representa −(2 + 1/4) = −9/4, que vira −9:4. Em muitas aplicações práticas de razão (como composições químicas ou receitas), trabalhar com negativa não faz sentido, mas em vetores, variações e movimentos com direção, o sinal pode ser relevante. Avalie o contexto antes de aceitar ou rejeitar uma razão negativa.

Zero é outro ponto a verificar. 0 1/3 não existe, pois fração mista supõe parte fracionária própria acoplada a um inteiro. Se a intenção for 0 como valor total, a fração imprópria seria 0/c e a razão resultaria 0:c → 0:1 após simplificar (quando c ≠ 0). De novo, cheque a coerência com a situação do problema.

Unidades e interpretação: se a razão comunica uma taxa (ex.: km:h), mantenha a ordem “quantidade por unidade” coerente com o enunciado. Se o texto pede “litros de x para litros de y”, não troque a ordem ao converter — isso altera a leitura e o sentido da proporção final.

Situações contextualizadas: como isso aparece na prática

Receitas de cozinha: suponha que a quantidade de farinha seja 1 1/2 xícaras e a de açúcar, 1 xícara. Converter 1 1/2 para 3/2 e, depois, 3:2, permite expressar a mistura como 3 partes de farinha para 2 partes de açúcar. Assim, se você dobrar a receita, mantém a mesma leitura proporcional sem confusão de unidades.

Escalas de mapas: imagine que uma medida em um mapa é 2 3/4 centímetros e corresponde a uma distância real de 11 quilômetros. Converter 2 3/4 → 11/4 → 11:4 ajuda a relacionar “mapa:real” com clareza, desde que você posicione corretamente qual termo representa o desenho e qual representa a realidade.

Química e soluções: uma solução pode pedir 3 1/3 partes de solvente para cada 1 parte de soluto. Reescrevendo 3 1/3 como 10/3, a razão fica 10:3. Com isso, é fácil escalar para qualquer volume: para cada 13 unidades totais (10 + 3), mantenha 10 de solvente e 3 de soluto.

Estatísticas esportivas: o desempenho de um time pode ser descrito como 2 1/2 vitórias “equivalentes” a cada 1 derrota, quando ponderamos empates como frações. Convertendo 2 1/2 → 5/2 → 5:2, a comparação fica padronizada e pronta para ser confrontada com outras equipes ou temporadas.

Educação financeira: às vezes se compara “parcelas pagas” para “parcelas totais” com frações mistas devido a juros ou descontos proporcionais. Transformar a fração mista em razão padroniza as proporções de pagamento e facilita simulações de replanejamento de dívidas.

Do decimal à razão (via fração) e conexões úteis

Embora nosso foco seja a fração mista, aparece com frequência a necessidade de lidar com decimais. O truque é converter o decimal em fração, depois seguir a mesma lógica. Ex.: 1,75 = 7/4 → 7:4. E se o enunciado “esconde” uma fração mista em forma decimal, o caminho continua curto e seguro.

O inverso também funciona: se uma razão é 7:3, escreva como 7/3 e converta para misto (2 1/3) ou decimal (≈ 2,333…), dependendo do que a questão pede. Esses vai-e-vens treinam sua flexibilidade com representações equivalentes.

Para razões que envolvem porcentagens, converta a porcentagem em fração primeiro. Por exemplo, 150% = 3/2, então a razão correspondente é 3:2. Quando a questão mistura frações mistas e porcentagens, padronizar tudo em frações simplifica a leitura e a resolução.

Estratégias para evitar erros e ganhar velocidade

Padronize seu raciocínio: sempre transforme fração mista em imprópria antes de qualquer outra coisa. Essa rotina protege contra confusões entre numerador e denominador e corta o risco de inverter a ordem sem perceber.

Marque a ordem pedida: se o problema solicitar “A para B”, anote A:B à margem antes de começar a converter. Esse rascunho simples ajuda a manter a consistência até o fim do cálculo.

Treine a simplificação: tenha em mente tabelas mentais de múltiplos e divisores comuns (2, 3, 4, 5, 6, 8, 9). Reconhecer rapidamente quando é possível dividir por 3 (soma dos dígitos múltipla de 3) ou por 9 acelera a redução da razão.

Cheque com uma “regra de três interna”: multiplique cruzado a fração imprópria e a razão proposta. Se 7/3 virou 7:3, pensar 7×? = 3×? não aponta inconsistência; ao contrário, reforça que ambos representam a mesma proporção em formatos diferentes.

Perguntas frequentes (FAQ) rápidas

Preciso sempre simplificar a razão final? Em contexto acadêmico, sim: a forma reduzida é o padrão. Em relatórios práticos, pode-se manter termos grandes se forem mais informativos (por exemplo, manter unidades explícitas), mas a simplificação continua recomendada para clareza.

Posso inverter a ordem para “deixar bonito”? Não. A ordem tem significado. Inverter 3:2 para 2:3 altera a comparação. Só inverta se o enunciado pedir a razão na ordem oposta ou se for relevante mudar a perspectiva explicitamente.

Como lido com fração mista negativa? Coloque o sinal no resultado final: −2 1/4 → −9/4 → −9:4. Em muitos contextos de proporção física, razões negativas não se aplicam; avalie a coerência com o problema antes de aceitar o sinal.

Quando usar decimal em vez de razão? Se a questão pede porcentagens, taxas contínuas ou aproximações, decimais podem ser mais práticos. Mas a razão é a linguagem mais direta para comparar partes de um todo ou de conjuntos distintos sem necessidade de arredondamentos.

Exercícios guiados para fixar

1) Converta 2 4/6 em razão. Solução comentada: 2 4/6 = (2×6 + 4)/6 = 16/6 → 8:3 após dividir por 2. Logo, 8:3.

2) Converta 5 3/9 em razão. Passos: 5 3/9 = (5×9 + 3)/9 = 48/9 → 16:3 (divide por 3).

3) Dada a razão 15:6, reescreva como fração mista. Caminho: 15:6 = 15/6 → divide por 3 → 5/2 → 2 1/2.

4) Em uma mistura, para cada 1 1/3 de produto A, temos produto B na razão A:B. Conversão: 1 1/3 = 4/3 → razão A:B = 4:3 (se B = 1 unidade). Sempre confira a ordem indicada na pergunta.

5) Verificação com contexto: uma escala diz que 1 1/4 cm no mapa representa 5 km reais. Converta 1 1/4 → 5/4 → 5:4 e rotule corretamente o que é “mapa” e o que é “real”. Isso evita confusões na aplicação da escala.

Dicas finais de estudo e aplicação

Monte um “kit mental”: tenha na ponta da língua pequenos blocos de cálculo, como 1 1/2 → 3:2, 2 1/4 → 9:4, 3 1/3 → 10:3. Com a prática, esse repertório acelera a identificação de padrões e reduz o esforço cognitivo em provas.

Use tecnologia a seu favor: uma calculadora com função de frações pode converter rapidamente o misto em imprópria, liberando tempo para checar ordem, contexto e simplificação. Só não deixe a ferramenta substituir a compreensão do processo.

Explique para alguém: ensinar o método a outra pessoa é um excelente teste de domínio. Ao verbalizar os passos, você torna explícitas as justificativas e consolida a sequência lógica de conversão e checagem.

Organize seus rascunhos: escreva a:b logo no início com os rótulos do enunciado (A para B). Essa anotação simples funciona como “trilho” para seu raciocínio, diminuindo o risco de inverter posições no resultado final.

Dominar a conversão de frações mistas para razões libera você para concentrar energia no que realmente importa: interpretar o problema, comunicar proporções com clareza e aplicar a comparação correta. Com o hábito de transformar o misto em imprópria, respeitar a ordem pedida e simplificar com o MDC, a técnica se torna automática e confiável, servindo tanto para exercícios quanto para aplicações do dia a dia em que a notação a:b diz mais, de forma mais rápida, do que qualquer outra representação numérica.