Como preencher os números que faltam em frações: guia completo

Início » Ciência » Matemática » Como preencher os números que faltam em frações: guia completo

Quando um enunciado pede “como preencher os números que faltam em frações”, na prática está pedindo que você reconheça frações equivalentes e use proporcionalidade. Isso significa descobrir qual numerador ou denominador completa a igualdade sem alterar o valor da fração, o que se faz multiplicando ou dividindo numerador e denominador por um mesmo número (diferente de zero) ou, se preferir, usando multiplicação cruzada.

Nesse caminho, entender frações, frações equivalentes e números decimais ajuda demais, porque tudo conversa entre si. Converter fração para decimal (ou percentual) serve como conferência rápida, além de facilitar comparações e operações. A seguir, você encontra um guia completo — direto ao ponto — com definições, exemplos, estratégias e exercícios resolvidos.

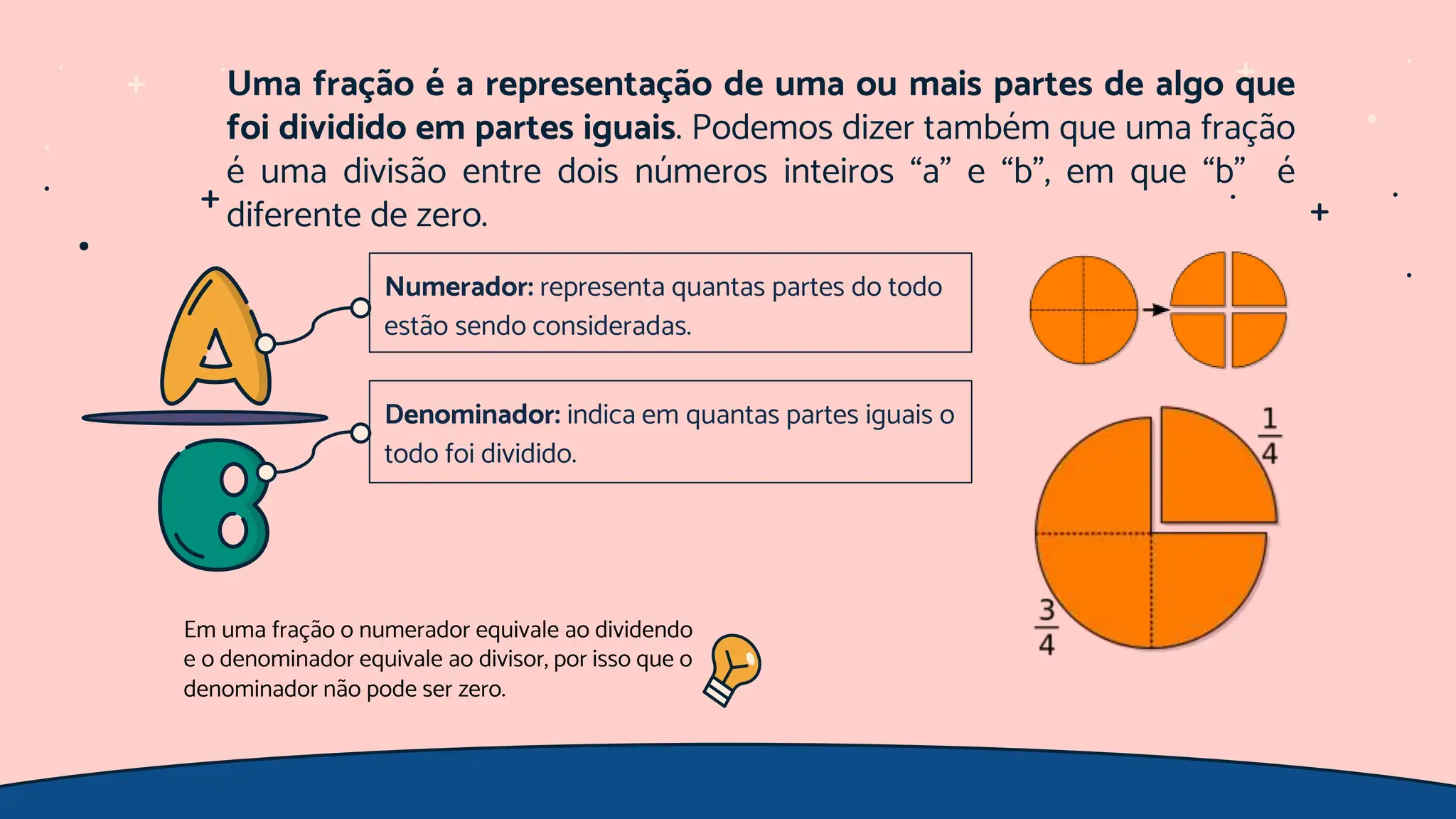
O que é “completar números que faltam” em frações?

Antes de mais nada, vale relembrar a anatomia de uma fração: o número de cima é o numerador e o de baixo é o denominador. Completar um valor que falta (por exemplo, ?/10 ou 3/?) significa encontrar um par equivalente que mantenha o mesmo valor da fração.

O mesmo raciocínio vale para 3/4 e 9/12: dividindo 9/12 por 3 (em cima e embaixo), chegamos a 3/4. As representações são distintas, mas o resultado numérico é idêntico.

Para gerar novas frações equivalentes, basta multiplicar (ou dividir) numerador e denominador pelo mesmo fator, diferente de zero. Esse procedimento não altera o valor da fração, apenas sua “cara”.

Um exemplo clássico é 5/8: multiplicando por 3 em cima e embaixo, viramos 15/24; repetindo o mesmo fator 3 sobre 15/24, chegamos a 45/72. Assim, 5/8, 15/24 e 45/72 são equivalentes. Se quisermos conferir, é só simplificar ao máximo — voltamos a 5/8.

Quando nenhuma simplificação adicional é possível, dizemos que a fração é irredutível. Por exemplo, 5/8 é irredutível, enquanto frações que ainda podem ser simplificadas são chamadas de redutíveis.

Passo a passo: estratégias para achar o número que falta

1) Proporção direta: escreva a igualdade entre frações e use multiplicação cruzada. Se a/ b = c/ d, então a·d = b·c. Com isso, você resolve rapidamente o valor desconhecido.

2) Escala por fator: identifique de que número um denominador (ou numerador) foi multiplicado para virar o outro. Repita o mesmo fator no numerador (ou denominador) e encontre o valor que falta.

3) Conferência decimal: converta para decimal sempre que puder. Se duas frações têm a mesma forma decimal (ex.: 0,625), elas são equivalentes, o que confirma seu preenchimento.

Exemplo rápido (múltipla escolha): Qual é equivalente a 2/5? Alternativas: 4/10; 4/12; 5/10; 5/8; 2/19. Multiplicando 2/5 por 2 em cima e embaixo, obtemos 4/10, que é a correta. As outras não preservam a mesma razão.

Outro exemplo: escreva três frações equivalentes a 9/10. Multiplicando por 2, 3 e 4, ficam 18/20, 27/30 e 36/40. Qualquer fator não nulo serve.

Checagem decimal: 5/8 = 0,625. Se você completar algo como ?/8 para que seja equivalente a 5/8, deve obter 5/8 novamente quando simplificar, e a forma decimal precisa bater: 0,625.

Noções essenciais de frações e números decimais

Frações e decimais aparecem em situações do dia a dia, do peso do café ao troco no caixa. A notação X/Y é uma forma prática de representar divisão, desde que Y seja diferente de zero.

Historicamente, o ser humano introduziu frações quando precisou medir e descrever partes de medidas. Egípcios usavam sobretudo frações unitárias (1/2, 1/3, 1/4, …), e compunham outras como 5/6 = 1/2 + 1/3.

Já os babilônios trabalhavam muito com denominador 60, possivelmente por sua alta quantidade de divisores inteiros. Os romanos, por sua vez, eram fãs do 12 como denominador, também por razões de divisibilidade. A forma atual de escrever frações se consolidou no século XVI.

Os números decimais surgiram a partir das frações decimais. Por exemplo, 1/2 equivale a 5/10 e, portanto, ao decimal 0,5. Esse salto encurtou cálculos e, com o sistema métrico, popularizou-se muito além das aplicações astronômicas.

Em 1585, Simon Stevin propôs um método para realizar operações apenas com inteiros, sem usar frações, marcando posições decimais de forma engenhosa. Mais tarde, em 1617, John Napier sugeriu o uso do ponto ou da vírgula para separar a parte inteira da parte decimal, notação que usamos até hoje (no Brasil e em Portugal, com vírgula).

Frações decimais e escrita em forma decimal

Chamamos de fração decimal aquela cujo denominador é potência de 10 (10, 100, 1000, …). Exemplos: 1/10, 3/100, 23/100, 1/1000, 1/10³.

Toda fração decimal pode ser representada por um número decimal, com parte inteira (PI) e parte decimal (PD) separadas por vírgula. Veja 127/100: escrevemos 1,27, pois 127/100 = 100/100 + 27/100 = 1 + 0,27 = 1,27.

Outro caso: 8/10 = 0,8. Como o numerador é menor que o denominador, trata-se de um número menor que 1, o que já percebemos visualmente pela vírgula.

Como ler decimais? Observe a posição da vírgula, identifique casas decimais e nomeie-as. Exemplos práticos de leitura:

• 0,6: “seis décimos”.
• 0,37: “trinta e sete centésimos”.
• 0,189: “cento e oitenta e nove milésimos”.
• 3,7: “três inteiros e sete décimos”.
• 13,45: “treze inteiros e quarenta e cinco centésimos”.
• 130,824: “cento e trinta inteiros e oitocentos e vinte e quatro milésimos”.

Na prática, transformar fração decimal em número decimal é efetuar a divisão do numerador pelo denominador (com zeros indicando casas). Por exemplo: 130/100 = 1,30; 987/1000 = 0,987; 5/1000 = 0,005.

No sentido inverso, para transformar decimal em fração decimal, coloque no numerador o número sem vírgula e, no denominador, 1 seguido do número de zeros igual ao de casas decimais. Exemplos: 0,5 = 5/10; 0,05 = 5/100; 2,41 = 241/100; 7,345 = 7345/1000.

Operações com decimais (e por que elas ajudam com frações equivalentes)

Acrescentar zeros à direita, depois do último algarismo decimal não nulo, não altera o valor. Logo, 0,5 = 0,50 = 0,500; e 1,0002 = 1,00020; e assim por diante. Essa ideia volta quando alinhamos vírgulas em somas e subtrações.

Multiplicação por potências de 10 desloca a vírgula para a direita: 7,4 × 10 = 74; 7,4 × 100 = 740; 7,4 × 1000 = 7400. Dividir por 10, 100, 1000 desloca para a esquerda: 247,5 ÷ 10 = 24,75; ÷ 100 = 2,475; ÷ 1000 = 0,2475.

Na adição e subtração de decimais, primeiro igualamos o número de casas (acrescentando zeros) e alinhamos vírgulas e colunas. Exemplos: 2,4 + 1,713 = 2,400 + 1,713 = 4,113; 2,4 − 1,713 = 0,687.

Para multiplicar decimais, há dois jeitos: converter cada um em fração decimal e multiplicar numeradores e denominadores; ou multiplicar como inteiros e colocar no produto o total de casas decimais somadas. Exemplo icônico: 2,25 × 3,5 = (225/100) × (35/10) = 7875/1000 = 7,875.

Na divisão de decimais, explore a ideia de que multiplicar numerador e denominador por 10, 100, 1000 não altera o quociente. Assim, 3,6 ÷ 0,4 = (3,6 × 10) ÷ (0,4 × 10) = 36 ÷ 4 = 9. E 0,35 ÷ 7 = (0,35 × 100) ÷ (7 × 100) = 35/700 = 5/100 = 0,05.

E quando o divisor é maior que o dividendo? Transforme o dividendo em décimos, centésimos etc. Por exemplo, 35 ÷ 700 vira 3500 ÷ 700 (multiplicamos o dividendo por 100), garantindo quociente 5, mas ajustando para 0,05 porque deslocamos a vírgula. É a mesma ideia de anexar zeros e reposicionar a vírgula.

Um caso clássico é 10 ÷ 16, que não dá quociente inteiro. Procedendo na divisão, obtemos 0,625: 10 vira 100 (colocamos vírgula no quociente), 100 ÷ 16 = 6, resto 4; desce um zero (40 ÷ 16 = 2, resto 8); desce outro zero (80 ÷ 16 = 5, resto 0). Resultado final: 0,625.

Comparação de decimais e o elo com porcentagem

Para comparar decimais, comece pela parte inteira: quem tem parte inteira maior é maior. Assim, 4,1 > 2,76 e 3,7 < 5,4.

Se as partes inteiras forem iguais, iguale as casas decimais adicionando zeros e compare as partes decimais como se fossem inteiros. Exemplos: 12,4 > 12,31 (escrevendo 12,40 > 12,31); 8,032 < 8,47 (ou 8,032 < 8,470); e 4,3 = 4,3.

Porcentagem é uma razão com denominador 100. Em linguagem fracionária, 30% é 30/100. Isso facilita conversões e verificações de equivalência.

Aplicações rápidas: se 30% dos alunos são meninas, a razão é 30 para cada 100. Para calcular 40% de R$ 300, usamos a proporção 40/100 = X/300. Fazendo cruzado: 100·X = 12.000 ⇒ X = 120. Logo, 40% de 300 é 120.

Outro exemplo: li 45% de um livro de 200 páginas. Como 45/100 = X/200, segue 100·X = 9.000 ⇒ X = 90; faltam 200 − 90 = 110 páginas. Perceba como percentuais, frações e decimais convergem.

Exercícios resolvidos: preenchendo números que faltam

Exercício 1. Qual fração é equivalente a 2/5? Alternativas: a) 4/10 b) 4/12 c) 5/10 d) 5/8 e) 2/19. Correta: 4/10. Justificativa: 2/5 × 2/2 = 4/10. As demais não mantêm a mesma razão (por exemplo, 5/10 = 1/2, que não é 2/5).

Exercício 2. Escreva três frações equivalentes a 9/10. Multiplique por 2, 3 e 4: 18/20, 27/30, 36/40. Você também poderia usar 90/100, 900/1000 etc., e conferir convertendo para 0,9.

Conferindo com decimais: 2/5 = 0,4; 4/10 = 0,4. Se o decimal bate, a equivalência está confirmada. Faça o mesmo com 9/10 = 0,9, e com 18/20 = 0,9, 27/30 = 0,9…

Estratégia geral para ?/b = a/d: use cruzado. Se ?/8 = 5/8, então 8·? = 8·5 ⇒ ? = 5. Se 3/? = 9/12, então 3·12 = 9·? ⇒ 36 = 9·? ⇒ ? = 4, logo 3/4.

Para fechar, lembre-se: se a fração já está irredutível, como 5/8, a forma decimal (0,625) é uma ótima checagem. Qualquer forma equivalente — 10/16, 45/72, 0,625 — representa a mesma quantidade, e isso é exatamente o que queremos quando “preenchemos números que faltam”.

Ao dominar equivalência de frações, conversões para decimais, regras de comparação e operações básicas, você ganha autonomia para resolver desde questões simples de completar numerador/denominador até problemas práticos com porcentagens. Use multiplicação cruzada para encontrar o termo desconhecido, simplifique para checar a forma irredutível e valide com a forma decimal quando fizer sentido; com essas três frentes, as frações “com lacunas” deixam de ser um mistério e viram rotina resolúvel.