Em matemática, o domínio e o contradomínio de uma função são conceitos fundamentais que nos ajudam a entender o comportamento e as restrições de uma relação matemática. O domínio de uma função é o conjunto de todos os valores de entrada para os quais a função está definida, enquanto o contradomínio é o conjunto de todos os valores de saída possíveis da função.
Por exemplo, considere a função f(x) = √x. Neste caso, o domínio da função é o conjunto de todos os números reais não negativos, pois a raiz quadrada de um número negativo não está definida nos reais. Já o contradomínio da função é o conjunto de todos os números reais não negativos, pois a raiz quadrada de qualquer número real não negativo é também um número real não negativo.
É importante entender o domínio e o contradomínio de uma função para garantir que a função esteja bem definida e para interpretar corretamente seus resultados.
Identificando domínio e contradomínio em funções de maneira simples e prática.
Domínio e contradomínio são conceitos fundamentais em matemática que nos ajudam a entender o comportamento das funções. O domínio de uma função é o conjunto de todos os valores de entrada possíveis, ou seja, os valores que podem ser substituídos na função. Já o contradomínio é o conjunto de todos os valores de saída possíveis, ou seja, os valores que a função pode assumir após a substituição dos valores de entrada.
Para identificar o domínio de uma função, devemos observar quais valores podem ser utilizados como entrada na função sem causar problemas, como divisão por zero ou raízes quadradas de números negativos. Já o contradomínio é determinado pela faixa de valores que a função pode assumir como saída.
Por exemplo, considere a função f(x) = 2x + 1. O domínio dessa função é o conjunto de todos os números reais, pois podemos substituir qualquer número real em x sem restrições. Já o contradomínio é o conjunto de todos os números reais, pois a função pode assumir qualquer valor real como saída.
Agora, vamos analisar a função g(x) = √x. O domínio dessa função é o conjunto de todos os números reais maiores ou iguais a zero, pois não podemos calcular a raiz quadrada de um número negativo. O contradomínio é o conjunto de todos os números reais maiores ou iguais a zero, pois a função só pode assumir valores não negativos como saída.
Em resumo, o domínio de uma função determina quais valores podem ser usados como entrada, enquanto o contradomínio define quais valores a função pode assumir como saída. Entender esses conceitos é essencial para analisar e interpretar o comportamento das funções matemáticas.
Entenda a distinção entre domínio e contradomínio em apenas algumas palavras.
O domínio de uma função é o conjunto de todos os valores de entrada possíveis, enquanto o contradomínio é o conjunto de todos os valores de saída possíveis. Por exemplo, na função f(x) = x², o domínio é todos os números reais, enquanto o contradomínio é todos os números reais não negativos.
É importante notar que o domínio é o conjunto de valores para os quais a função está definida, enquanto o contradomínio é o conjunto de valores que a função pode assumir. Por exemplo, na função f(x) = 1/x, o domínio é todos os números reais exceto zero, enquanto o contradomínio é todos os números reais.
Em resumo, o domínio é o conjunto de valores de entrada válidos, enquanto o contradomínio é o conjunto de valores de saída possíveis. Ambos são fundamentais para entender e analisar uma função matemática.
Entendendo o intervalo de valores que uma função pode assumir em sua entrada.
Quando estudamos uma função, é importante compreender não apenas o seu domínio, que são os valores que a variável de entrada pode assumir, mas também o seu contradomínio, que são os valores que a variável de saída pode assumir. O contradomínio é o conjunto de todos os possíveis valores que a função pode retornar, enquanto o domínio é o conjunto de valores que a função pode receber como entrada.
Por exemplo, considere a função f(x) = x². O domínio dessa função é o conjunto dos números reais, pois qualquer número real pode ser elevado ao quadrado. Já o contradomínio é o conjunto dos números reais não negativos, pois o quadrado de qualquer número real será sempre não negativo.
Outro exemplo seria a função g(x) = sen(x). Neste caso, o domínio é o conjunto dos números reais, pois o seno de qualquer número real está definido. O contradomínio, por sua vez, é o intervalo fechado entre -1 e 1, pois o seno de qualquer número real estará sempre compreendido nesse intervalo.
Portanto, entender o intervalo de valores que uma função pode assumir em sua entrada é fundamental para compreender o seu comportamento e suas propriedades. O domínio e o contradomínio são conceitos essenciais na análise de funções matemáticas.
Conceito de contra domínio na matemática: entenda sua importância e aplicação prática.
O conceito de contra domínio em matemática é fundamental para compreender a relação entre os elementos de um conjunto de partida (domínio) e os elementos de um conjunto de chegada (contra domínio) em uma função. Enquanto o domínio representa o conjunto de valores de entrada para uma função, o contra domínio representa o conjunto de valores possíveis de saída da função.
Em termos simples, o contra domínio é o conjunto de todos os valores que a função pode assumir. Por exemplo, se tivermos uma função f(x) = x², o domínio seria o conjunto dos números reais, enquanto o contra domínio seria o conjunto dos números reais não negativos.
A importância do contra domínio reside no fato de que ele nos permite determinar se a função está bem definida e se todas as possíveis saídas estão sendo consideradas. Além disso, o contra domínio nos ajuda a compreender o alcance da função e a interpretar seus resultados de forma mais precisa.
Na prática, o conhecimento do contra domínio de uma função é essencial para garantir que a função seja corretamente aplicada em problemas do mundo real. Por exemplo, ao modelar o crescimento populacional de uma cidade, é crucial definir corretamente o contra domínio da função que descreve esse crescimento para evitar resultados inconsistentes.
Em resumo, o contra domínio é uma parte essencial da teoria das funções matemáticas, pois nos permite entender e interpretar corretamente o comportamento das funções em diferentes situações. Ao considerar tanto o domínio quanto o contra domínio de uma função, podemos garantir uma análise mais completa e precisa de seus resultados.
Domínio e Contradomain de uma função (com exemplos)
Os conceitos de domínio e domínio de uma função são comumente ensinados nos cursos de cálculo ministrados no início das carreiras universitárias.
Antes de definir o domínio e o domínio, você deve saber o que é uma função. Uma função f é uma lei (regra) de correspondência feita entre os elementos de dois conjuntos.

O conjunto do qual os elementos são escolhidos é chamado de domínio da função e o conjunto para o qual esses elementos são enviados por meio de f é chamado de contra-domínio.
Em matemática, uma função com domínio A e contra domínio B é denotada pela expressão f: A → B.
A expressão anterior diz que os elementos do conjunto A são enviados para o conjunto B, seguindo a lei da correspondência f.
Uma função atribui a cada elemento do conjunto A um único elemento do conjunto B.
Domínio e Contradomain
Dada uma função real de uma variável real f (x), assume-se que o domínio da função será todos esses números reais, de modo que, quando avaliado em f, o resultado seja um número real.
Geralmente, o contra-domínio de uma função é o conjunto de números reais R. O contra-domínio também é chamado de conjunto de chegada ou co-domínio da função f.
A contradição de uma função é sempre R?
Não. Enquanto a função não for estudada em detalhes, o conjunto de números reais R. é geralmente tomado como dominância.
Mas uma vez que a função foi estudada, um conjunto mais adequado pode ser tomado como um contra-domínio, que será um subconjunto de R.
O conjunto apropriado mencionado no parágrafo anterior corresponde à imagem da função.
A definição da imagem ou intervalo de uma função f refere-se a todos os valores resultantes da avaliação de um elemento do domínio em f.
Exemplos
Os exemplos a seguir ilustram como calcular o domínio de uma função e sua imagem.
Exemplo 1
Seja f uma função real definida por f (x) = 2.
O domínio de f é todo número real, de modo que, quando avaliado em f, o resultado é um número real. A dominância no momento é igual a R.
Como a função fornecida é constante (sempre igual a 2), deve ser independente do número real escolhido, pois ao avaliar em f o resultado sempre será igual a 2, que é um número real.
Portanto, o domínio da função fornecida é todos os números reais; isto é, A = R.
Agora que se sabe que o resultado da função é sempre igual a 2, a imagem da função é apenas o número 2; portanto, o domínio da função pode ser redefinido como B = Img (f) = {2}.
Portanto, f: R → {2}.
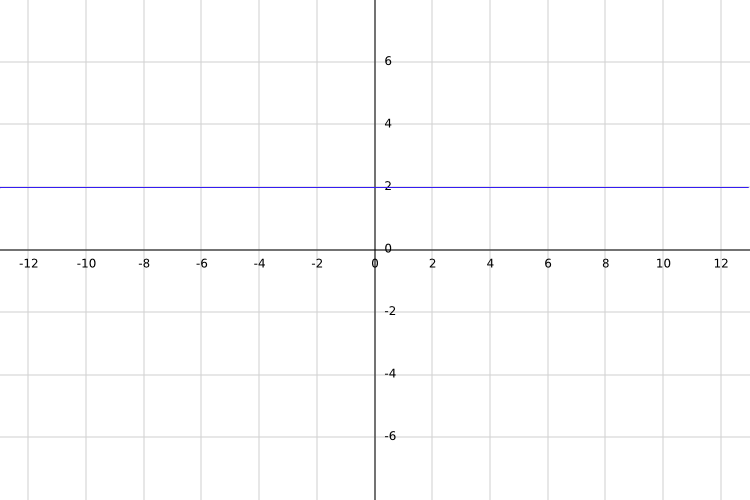
Exemplo 2
Seja g uma função real definida por g (x) = √x.
Enquanto a imagem de g é desconhecida, a contradição de g é B = R.
Com esta função, deve-se levar em consideração que raízes quadradas são definidas apenas para números não negativos; isto é, para números maiores ou iguais a zero. Por exemplo, √-1 não é um número real.
Portanto, o domínio da função g deve ser todos os números maiores ou iguais a zero; isto é, x ≥ 0.
Portanto, A = [0, + ∞).
Para calcular o intervalo, deve-se observar que qualquer resultado de g (x), sendo uma raiz quadrada, sempre será maior ou igual a zero. Ou seja, B = [0, + ∞).
Em conclusão, g: [0, + ∞) → [0, + ∞).

Exemplo 3
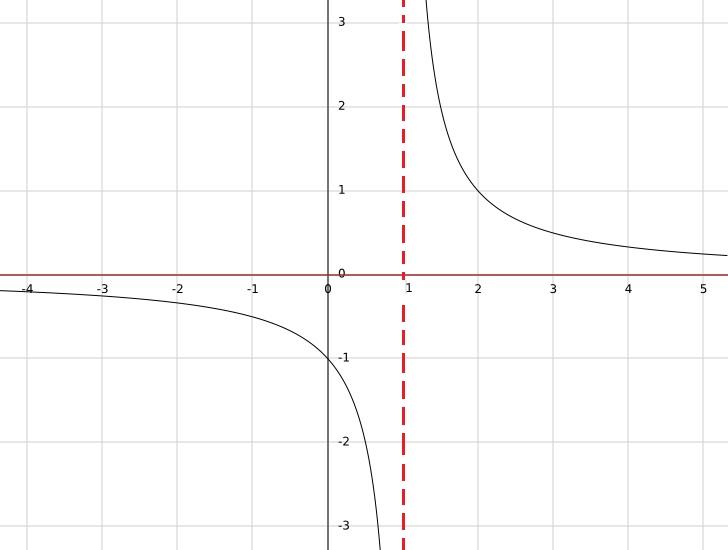
Se você possui a função h (x) = 1 / (x-1), essa função não está definida para x = 1, pois zero seria obtido no denominador e a divisão por zero não está definida.
Por outro lado, para qualquer outro valor real, o resultado será um número real. Portanto, o domínio é todo real, exceto aquele; isto é, A = R {1}.
Da mesma forma, pode-se observar que o único valor que não pode ser obtido como resultado é 0, pois para uma fração ser igual a zero, o numerador deve ser zero.
Portanto, a imagem da função é o conjunto de todos os reais, exceto zero, então B = R {0} é tomado como dominância.
Em conclusão, h: R {1} → R {0}.
Observações
O domínio e a imagem não precisam ter o mesmo conjunto, como demonstrado nos exemplos 1 e 3.
Quando uma função é plotada no plano cartesiano, o domínio é representado pelo eixo X e o domínio ou intervalo do contador é representado pelo eixo Y.
Referências
- Fleming, W. & Varberg, DE (1989). Matemática Pré-cálculo. Prentice Hall PTR.
- Fleming, W. & Varberg, DE (1989). Matemática pré-cálculo: uma abordagem de resolução de problemas (2, Illustrated ed.). Michigan: Prentice Hall.
- Fleming, W. & Varberg, D. (1991). Álgebra e trigonometria com geometria analítica. Pearson Education.
- Larson, R. (2010). Pré-cálculo (8 ed.). Cengage Learning
- Leal, JM e Viloria, NG (2005). Geometria analítica plana. Mérida – Venezuela: Editorial Venezolana CA
- Pérez, CD (2006). Pré-cálculo Pearson Education.
- Purcell, EJ, Varberg, D. & Rigdon, SE (2007). Cálculo (Nona ed.). Prentice Hall.
- Saenz, J. (2005). Cálculo diferencial com funções transcendentes iniciais para Ciência e Engenharia (Segunda Edição, ed.). Hipotenusa
- Scott, CA (2009). Cartesian Plane Geometry, Parte: Analytical Conics (1907) (reimpressão ed.). Fonte de Raios
- Sullivan, M. (1997). Pré-cálculo Pearson Education.