A geometria analítica é um ramo da matemática que combina conceitos da geometria euclidiana com técnicas da álgebra, permitindo a representação de figuras geométricas por meio de equações algébricas. Esta área de estudo foi desenvolvida no século XVII por René Descartes e Pierre de Fermat, revolucionando a forma como se abordava a geometria.
A geometria analítica tem diversas aplicações em áreas como engenharia, física, computação gráfica, entre outras. Ela é utilizada para resolver problemas geométricos de forma mais eficiente e precisa, permitindo a análise de formas e estruturas complexas de maneira mais sistemática.
Ao longo dos anos, a geometria analítica tem se mostrado uma ferramenta fundamental para o desenvolvimento de diversas áreas do conhecimento, possibilitando avanços significativos em diversas áreas da ciência e da tecnologia.
Aplicações práticas da geometria analítica em diversas áreas do conhecimento e da tecnologia.
A geometria analítica é uma ferramenta poderosa que tem aplicações práticas em diversas áreas do conhecimento e da tecnologia. Desde a sua criação por René Descartes no século XVII, a geometria analítica tem sido fundamental para resolver problemas complexos em várias disciplinas.
Na matemática, a geometria analítica é amplamente utilizada para estudar formas e figuras geométricas. Por meio de coordenadas cartesianas, é possível representar geometricamente equações e funções matemáticas, facilitando a visualização e resolução de problemas. Além disso, a geometria analítica é essencial em áreas como álgebra linear, cálculo diferencial e integral.
Em física, a geometria analítica é aplicada na modelagem de fenômenos físicos. Por exemplo, na mecânica, as equações do movimento de corpos podem ser representadas geometricamente por meio de vetores e coordenadas cartesianas. Isso facilita o entendimento e a previsão do comportamento de sistemas físicos complexos.
Nas engenharias, a geometria analítica é fundamental para o projeto e a análise de estruturas e sistemas. Por exemplo, na engenharia civil, a geometria analítica é utilizada para determinar as dimensões e as propriedades de edifícios e pontes. Já na engenharia elétrica, as coordenadas cartesianas são essenciais para o projeto de circuitos elétricos e eletrônicos.
Na computação, a geometria analítica é crucial para o desenvolvimento de gráficos e animações em 2D e 3D. Por meio de algoritmos e equações matemáticas, é possível criar imagens digitais realistas e interativas. Além disso, a geometria analítica é utilizada em áreas como a visão computacional e o processamento de imagens.
Em resumo, a geometria analítica desempenha um papel fundamental em diversas áreas do conhecimento e da tecnologia. Suas aplicações práticas são vastas e essenciais para a resolução de problemas complexos. Portanto, o estudo e o domínio da geometria analítica são importantes para profissionais de diversas áreas, que buscam soluções precisas e eficientes para os desafios do mundo moderno.
Principais usos da geometria na prática: entenda suas aplicações fundamentais.
A geometria é uma área da matemática que estuda as propriedades do espaço e das figuras que o ocupam. Ela está presente em diversos aspectos de nossa vida cotidiana e desempenha um papel fundamental em diversas áreas do conhecimento. Vamos explorar os principais usos da geometria na prática e entender suas aplicações fundamentais.
Um dos principais usos da geometria é na arquitetura e engenharia civil. Arquitetos e engenheiros utilizam conceitos geométricos para projetar construções, calcular áreas, volumes e distâncias, garantindo que as estruturas sejam seguras e funcionais. Além disso, a geometria é essencial na criação de mapas, plantas baixas e projetos de urbanismo.
Outra aplicação importante da geometria é na indústria, especialmente na fabricação de peças e componentes. Engenheiros mecânicos e projetistas utilizam a geometria para criar modelos tridimensionais, calcular tolerâncias e realizar simulações de montagem. A geometria também é fundamental na área da robótica, contribuindo para o desenvolvimento de sistemas de visão computacional e controle de movimento.
Além disso, a geometria tem aplicações em diversas áreas da ciência, como a física, a química e a biologia. Pesquisadores utilizam conceitos geométricos para descrever fenômenos naturais, modelar moléculas e estudar a forma de organismos vivos. A geometria também é essencial na astronomia, na geografia e em outras disciplinas que envolvem a análise e representação do espaço.
Em resumo, a geometria é uma ferramenta poderosa que desempenha um papel fundamental em nossa sociedade. Seja na construção de edifícios, na fabricação de produtos ou na investigação científica, os conceitos geométricos são essenciais para o progresso e a inovação em diversas áreas do conhecimento.
O objeto de estudo da geometria analítica são as relações entre pontos e figuras geométricas.
A geometria analítica é um ramo da matemática que estuda as relações entre pontos e figuras geométricas através de métodos algébricos. Utilizando coordenadas cartesianas, é possível representar geometricamente objetos matemáticos e resolver problemas de forma mais eficiente.
A história da geometria analítica remonta ao século XVII, com os trabalhos de Descartes e Fermat. Descartes foi o responsável por introduzir a ideia de coordenadas no plano, enquanto Fermat desenvolveu métodos para resolver equações polinomiais através da geometria.
As aplicações da geometria analítica são vastas e estão presentes em diversas áreas do conhecimento, como engenharia, física, computação e até mesmo em jogos de videogame. A capacidade de representar figuras geométricas de forma precisa e de resolver problemas complexos torna a geometria analítica uma ferramenta fundamental para o avanço da ciência e da tecnologia.
Em resumo, a geometria analítica estuda as relações entre pontos e figuras geométricas utilizando métodos algébricos, com aplicações em diversas áreas do conhecimento. Sua história remonta ao século XVII, com os trabalhos de Descartes e Fermat, e seu uso é fundamental para resolver problemas complexos e representar objetos matemáticos de forma eficiente.
Aplicações práticas da geometria analítica no cotidiano: descubra como usá-la em situações comuns.
A geometria analítica é uma área da matemática que combina técnicas da álgebra com a geometria para estudar formas geométricas no plano e no espaço. Muitas vezes, as pessoas podem pensar que a geometria analítica é uma disciplina abstrata e distante da realidade, mas na verdade ela possui diversas aplicações práticas no cotidiano.
Uma das aplicações mais comuns da geometria analítica é na construção civil. Engenheiros e arquitetos utilizam os conceitos dessa área da matemática para projetar e construir edifícios, pontes, estradas e outras estruturas. Através de coordenadas cartesianas e equações, é possível determinar a posição exata de cada elemento de uma construção, garantindo sua estabilidade e segurança.
Outra aplicação importante da geometria analítica é na navegação. GPS (Global Positioning System) e outros sistemas de localização utilizam cálculos baseados em coordenadas para determinar a posição de um objeto na terra. Graças à geometria analítica, é possível traçar rotas, calcular distâncias e chegar a destinos com precisão.
Além disso, a geometria analítica também é amplamente utilizada em áreas como a computação gráfica, a física, a engenharia mecânica e a robótica. Em todas essas áreas, os conceitos e técnicas da geometria analítica são essenciais para resolver problemas complexos e desenvolver novas tecnologias.
Portanto, podemos concluir que a geometria analítica não é apenas uma disciplina teórica, mas sim uma ferramenta poderosa e versátil que tem impacto direto em nossas vidas. Seja na construção de um prédio, na navegação por GPS ou no desenvolvimento de novas tecnologias, a geometria analítica está presente em muitas situações do nosso cotidiano.
Geometria analítica: quais estudos, história, aplicações
Noxa é um termo que serve para qualificar todo esse elemento que pode afetar um determinado organismo. Ao entrar em contato com esse fator, você é propenso a apresentar desequilíbrios físicos, psíquicos e sociais que afetam diretamente a saúde.
Um exemplo comum para ilustrar os danos que uma noxa pode causar pode ser o contato do homem com um vírus ou bactéria. Quando o noxa é introduzido no corpo, suas defesas o reconhecem para tentar mais tarde eliminar o desequilíbrio causado pela doença.
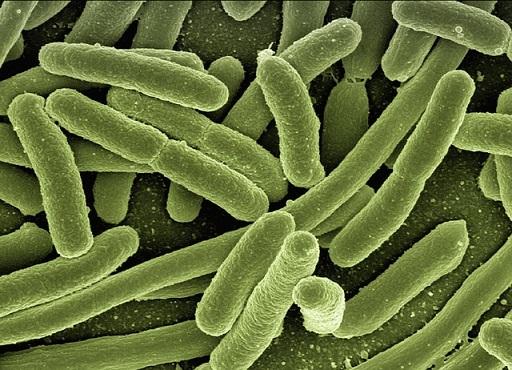
A transmissão de uma noxa é devida principalmente a três fatores: a suscetibilidade do organismo, as condições do ambiente e a interação que o indivíduo tem com o ambiente.
Existem três tipos de noxas: os biológicos, físico-químicos e os de natureza sociocultural. No caso deste último, alguns autores também incluem fatores psíquicos.
Tipos (características de cada)
As características mais importantes dos tipos de noxas são discutidas abaixo:
Biológico
-Eles também são chamados agentes patogenizados.
-Eles são considerados as principais causas das doenças, pois incluem vírus, bactérias e parasitas.
-Eles podem causar condições porque uma quantidade maior ou menor é encontrada no corpo. Isso significa que existem vírus e bactérias que podem ser benéficos para o corpo humano, mas que, se forem grandes ou baixos, podem causar sérios problemas de saúde.
-Os protozoários estão incluídos nesse grupo e podem atuar como consumidores, saprófitos e até parasitas. Eles podem causar doenças como malária ou doença de Chagas.
-Outro tipo de noxa biológica são os fungos unicelulares ou multicelulares. Isso pode causar problemas de pele e erupções cutâneas.
-Worms e worms também são nocivos que podem ser alojados no sistema digestivo, devido ao consumo de alimentos mal manipulados.
Físico-químico
-Neste grupo estão todos os derivados de substâncias químicas e agentes físicos potencialmente fatais para o homem.
- Físico: inclui mudanças bruscas de temperatura, pressão atmosférica, raios ultravioletas, raios X, pancadas e feridas, superexposição aos raios solares e radiação atômica.
- Produtos químicos: a causa pode ser o consumo ou inalação de substâncias tóxicas, como venenos, poluentes e picadas de animais peçonhentos.
Sociocultural (alguns autores também incluem noxas psíquicos):
-Eles podem incluir fatores internos (psicológicos) ou externos.
Eles exercem uma poderosa influência sobre o homem, embora ele não possa controlá-lo completamente.
-Eles refletem os problemas éticos, estéticos e morais de uma sociedade.
-Os indivíduos que sofrem deste tipo de noxas podem estar constantemente preocupados com o futuro.
– Suas conseqüências podem levar às seguintes situações: guerras, racismo, xenofobia, instabilidade econômica e judicial, desigualdade, insegurança contra o crime, dependência de drogas, pobreza, discriminação religiosa e desemprego.
De uma perspectiva mais pessoal, esses noxas também podem causar mudanças drásticas no estilo de vida e estados perenes de estresse, angústia e ansiedade.
Meios de transmissão de uma noxa
Nesse sentido, é importante levar em consideração três aspectos: o nível de vulnerabilidade do organismo, o ambiente em que está localizado e como se relaciona com o ambiente.
Devido ao exposto, dois tipos de meios de transmissão são indicados:
- Direto: não há presença de intermediários, pois a doença passa de um ser vivo para outro.
- Indireta: a transmissão da doença ocorre através de intermediários (também chamados de “vetores”.
Doenças causadas por noxas
Doenças infecciosas e contagiosas
Eles são produzidos por noxes biológicos. Um exemplo disso pode ser o sarampo, cuja causa é um vírus misto. Ele penetra no corpo através do nariz e garganta, através do ar.
Após um período de incubação de 10 dias, a doença se intensifica produzindo tosse, febre e marcas na pele. Outros exemplos dessas doenças, como influenza, cólera e meningite, também podem ser citados.
Doenças sociais
Aqueles que afetam tanto um coletivo quanto o indivíduo. Exemplos: tuberculose e peste negra.
Doenças parasitárias
Eles são transmitidos diretamente ou através de intermediários, chamados “vetores”. Essas doenças são causadas por parasitas externos, como piolhos (causando pediculose) ou trichinella spirales, que causa triquinose.
Doenças traumáticas
Ligadas às noxas físicas, são as causadas por acidentes como: fraturas, entorses e até contusões.
Doenças mentais
Eles têm a ver com as alterações produzidas no funcionamento mental dos indivíduos, para que afetem diretamente seu comportamento. Psicose e depressão são dois casos de condições particulares que estão muito presentes na sociedade atual.
Doenças degenerativas e funcionais
Nesse caso, inclui dois tipos: os produzidos pela alteração no funcionamento das células como o câncer e os correspondentes à falha no desempenho de órgãos como o diabetes.
Doenças congênitas e hereditárias
Os congênitos se manifestam durante o processo de gestação (por exemplo, malformações da coluna vertebral), enquanto os hereditários têm a ver com a transmissão de material genético dos pais para os filhos. Alguns exemplos deste caso são daltonismo e hemofilia.
Outros tipos de doenças
- Doenças autoimunes: manifestam-se pelas reações geradas pelo sistema imunológico do corpo.
- Doenças neurodegenerativas: são doenças causadas pela morte de neurônios cerebrais, assim como pelo resto do sistema nervoso.
Termos Associados
Há vários conceitos relacionados a este tópico:
Epidemiologia: ciência que estuda as causas e a distribuição de doenças em uma determinada população.
-Brote: início súbito e propagação progressiva de uma doença de uma maneira incomum que se estende em uma área.
Epidemia: refere-se ao aparecimento de uma doença que se manifesta em um grande número de pessoas por um período de tempo.
-Endêmico: tem a ver com o número de casos de uma doença que se manifesta em um determinado local de forma estacionária. Pode apresentar ligeiros níveis de flutuação durante um determinado período.
-Pandemia: é uma epidemia que transcende os limites de uma população, para se espalhar por vários países e outras áreas geográficas.
Referências
- O que é noxa? (sf). Em Conceptdefinition.de. Recuperado: 8 de outubro de 2018. Em Conceptdefinicion.de de conceptdefinicion.de.
- Doenças físicas Noxas. (sf). Em Xuletas. Recuperado: 8 de outubro de 2018. Em Xuletas de xuletas.es.
- Noxa (medicamento). (sf). Em Academic Retirado: 8 de outubro de 2018. No Acadêmico de esacademic.com.
- Noxa (medicamento). (sf). Em Química. Retirado: 8 de outubro de 2018. Em Química.É de Química.es.
- Noxa (sf). Na Wikipedia Retirado: 8 de outubro de 2018. Na Wikipedia, em es.wikipedia.org.