As Leis de Morgan são um conjunto de regras fundamentais da álgebra booleana, que descrevem como as operações lógicas de negação, conjunção e disjunção se comportam em relação à lógica de proposições. Essas leis são essenciais para simplificar expressões lógicas complexas, bem como para realizar operações de álgebra booleana em circuitos digitais e sistemas de computação. As Leis de Morgan foram formuladas pelo matemático britânico George Boole e levam o nome do matemático e lógico americano Augustus De Morgan, que contribuiu para sua popularização.
Entenda o teorema De Morgan: como ele funciona e por que é importante.
O teorema de Morgan é uma regra fundamental na lógica booleana que nos permite simplificar expressões lógicas complexas. Ele estabelece duas leis que relacionam operações de negação, conjunção e disjunção. Essas leis são essenciais para simplificar e transformar equações lógicas, tornando-as mais fáceis de entender e manipular.
As leis de Morgan afirmam que a negação de uma conjunção é equivalente à disjunção das negações das proposições individuais, e que a negação de uma disjunção é equivalente à conjunção das negações das proposições individuais. Em outras palavras, se tivermos duas proposições A e B, a negação de “A e B” é o mesmo que “não A ou não B”, e a negação de “A ou B” é o mesmo que “não A e não B”.
Essas leis são fundamentais para simplificar expressões lógicas e facilitar a análise de circuitos digitais, algoritmos e sistemas computacionais. Ao aplicar as leis de Morgan, podemos reduzir o número de operações lógicas necessárias para representar uma expressão, o que pode resultar em uma simplificação significativa e uma melhor compreensão do problema em questão.
Em resumo, o teorema de Morgan é uma ferramenta poderosa na lógica booleana que nos permite simplificar e transformar expressões lógicas complexas de forma eficiente. Compreender e aplicar essas leis é fundamental para qualquer pessoa que trabalhe com lógica, matemática, computação ou eletrônica digital.
Lei De Morgan: princípio fundamental para simplificar expressões lógicas.
A Lei de Morgan é um princípio fundamental na lógica booleana que permite simplificar expressões lógicas complexas. Ela é composta por duas regras principais: a primeira diz que a negação de uma conjunção é equivalente à disjunção das negações das proposições originais, e a segunda afirma que a negação de uma disjunção é igual à conjunção das negações das proposições originais.
Em outras palavras, a Lei de Morgan é uma ferramenta poderosa que nos ajuda a transformar expressões lógicas de uma forma para outra mais simples e de mais fácil compreensão. Ela é amplamente utilizada em áreas como a matemática, a informática e a eletrônica.
Por exemplo, se tivermos a expressão “A E B”, pela Lei de Morgan podemos reescrevê-la como “não A OU não B”. Da mesma forma, se tivermos a expressão “A OU B”, podemos transformá-la em “não A E não B”. Essas transformações nos permitem simplificar cálculos e análises lógicas de forma mais eficiente.
Em resumo, a Lei de Morgan é uma ferramenta essencial para simplificar expressões lógicas complexas, tornando-as mais fáceis de manipular e entender. É importante compreender e aplicar corretamente esse princípio para obter resultados precisos e eficientes em diversos contextos.
Qual é o propósito fundamental do teorema de De Morgan na lógica booleana?
O propósito fundamental do teorema de De Morgan na lógica booleana é fornecer uma maneira de simplificar expressões booleanas complexas. Este teorema estabelece uma relação entre as operações de negação, conjunção e disjunção, permitindo que expressões sejam reescritas de forma mais simples e fácil de serem avaliadas.
Em termos simples, o teorema de De Morgan afirma que a negação de uma conjunção é equivalente à disjunção das negações e a negação de uma disjunção é equivalente à conjunção das negações. Isso é extremamente útil na simplificação de expressões booleanas, pois permite transformar uma expressão complexa em uma forma mais simples, facilitando a análise e manipulação.
Portanto, o teorema de De Morgan é uma ferramenta essencial na lógica booleana, ajudando a simplificar expressões e tornar a manipulação de lógica mais eficiente e compreensível.
Qual foi o responsável pela criação da lei de Morgan?
A lei de Morgan, também conhecida como leis de Morgan, foi formulada pelo biólogo e geneticista Thomas Hunt Morgan. Morgan nasceu em 1866 nos Estados Unidos e dedicou sua carreira ao estudo da genética, realizando importantes experimentos com moscas-das-frutas.
As leis de Morgan são fundamentais na genética, pois descrevem o padrão de herança dos genes em organismos diploides. Elas estabelecem as relações entre os genes e seus alelos durante a segregação e a combinação gênica.
Um dos erros mais comuns cometidos ao estudar as leis de Morgan é confundir os conceitos de dominância e recessividade. É importante entender que os genes podem interagir de maneira complexa e que nem sempre um alelo é dominante sobre o outro.
Portanto, Thomas Hunt Morgan foi o responsável por formular as leis de Morgan, que continuam sendo fundamentais para o estudo da genética até os dias atuais. Seu trabalho revolucionou a forma como entendemos a herança genética e abriu caminho para novas descobertas na área.
Leis de Morgan
Os l olhos de Morgan são regras de inferência usadas na lógica proposicional, que estabelecem que o resultado de negar uma disjunção e um conjunto de proposições ou variáveis proposicionais. Essas leis foram definidas pelo matemático Augustus De Morgan.
As leis de Morgan representam uma ferramenta muito útil para provar a validade de um raciocínio matemático. Mais tarde, eles foram generalizados dentro do conceito de conjuntos pelo matemático George Boole.

Essa generalização feita por Boole é completamente equivalente às leis iniciais de Morgan, mas é desenvolvida especificamente para conjuntos e não para proposições. Essa generalização também é conhecida como leis de Morgan.
Revisão da lógica proposicional
Antes de ver quais são as leis de Morgan especificamente e como elas são usadas, é conveniente lembrar algumas noções básicas de lógica proposicional. (Para mais detalhes, consulte o artigo de lógica proposicional).
No campo da lógica matemática (ou proposicional), uma inferência é uma conclusão emitida a partir de um conjunto de premissas ou hipóteses. Essa conclusão, juntamente com as premissas mencionadas, dá origem ao que é conhecido como raciocínio matemático.
Esse raciocínio deve poder ser demonstrado ou negado; isto é, nem todas as inferências ou conclusões em um raciocínio matemático são válidas.
Falácia
Uma inferência falsa emitida a partir de certas suposições que são consideradas verdadeiras é conhecida como falácia. As falácias têm a particularidade de serem argumentos que parecem corretos, mas matematicamente não são.
A lógica proposicional é responsável por desenvolver e fornecer métodos por meio dos quais se possa, sem ambiguidade, validar ou refutar um raciocínio matemático; isto é, inferir uma conclusão válida a partir de premissas. Esses métodos são conhecidos como regras de inferência, das quais as leis de Morgan fazem parte.
Proposições
Os elementos essenciais da lógica proposicional são proposições. As propostas são afirmações sobre as quais se pode dizer se são válidas ou não, mas que não podem ser verdadeiras ou falsas ao mesmo tempo. Não deve haver ambiguidade nesta questão.
Assim como os números podem ser combinados através das operações de adição, subtração, multiplicação e divisão, as proposições podem ser operadas por meio do conectivo lógico conhecido (ou conectores): negação (¬, “não”), disjunção (V , “O”), conjunção (Ʌ, “y”), condicional (→, “sim … então …”) e bicondicional (↔, “sim, e somente se”).
Para trabalhar de maneira mais geral, em vez de considerar proposições específicas, são consideradas variáveis proposicionais que representam quaisquer proposições e geralmente são indicadas com letras minúsculas p, q, r, s, etc.
Uma fórmula proposicional é uma combinação de variáveis proposicionais através de alguns dos conectivos lógicos. Em outras palavras, é uma composição de variáveis proposicionais. Eles geralmente são indicados com letras gregas.
Diz-se que uma fórmula proposicional implica logicamente outra quando a última é verdadeira cada vez que a primeira é verdadeira. Isso é indicado por:

Quando a implicação lógica entre duas fórmulas proposicionais é recíproca – isto é, quando a implicação anterior também é válida na direção oposta – as fórmulas são consideradas logicamente equivalentes e denotadas por

A equivalência lógica é um tipo de igualdade entre fórmulas proposicionais e permite que uma seja substituída pela outra quando necessário.
Leis de Morgan
As leis de Morgan consistem em duas equivalências lógicas entre duas formas proposicionais, a saber:

Essas leis nos permitem separar a negação de uma disjunção ou conjunção, como negação das variáveis envolvidas.
A primeira pode ser lida da seguinte forma: a negação de uma disjunção é igual à conjunção das negações. E o segundo diz assim: a negação de uma conjunção é a disjunção das negações.
Em outras palavras, negar a disjunção de duas variáveis proposicionais é equivalente à conjunção das negações de ambas as variáveis. Da mesma forma, negar a conjunção de duas variáveis proposicionais é equivalente à disjunção das negações de ambas as variáveis.
Como mencionado anteriormente, a substituição dessa equivalência lógica ajuda a demonstrar resultados importantes, juntamente com as outras regras de inferência existentes. Com elas, você pode simplificar muitas fórmulas proposicionais, para que sejam mais úteis para trabalhar.
A seguir, é apresentado um exemplo de demonstração matemática usando regras de inferência, entre essas leis de Morgan. Especificamente, é mostrado que a fórmula:

É equivalente a:
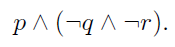
O último é mais simples de entender e desenvolver.
Demonstração

Vale ressaltar que a validade das leis de Morgan pode ser demonstrada matematicamente. Uma maneira é comparar suas tabelas de verdade.
Conjuntos
As mesmas regras de inferência e as noções de lógica aplicadas às proposições também podem ser desenvolvidas considerando conjuntos. Isso é conhecido como álgebra booleana, em homenagem ao matemático George Boole.
Para diferenciar casos, é necessário alterar a notação e transferir para conjuntos, todas as noções já vistas da lógica proposicional.
Um conjunto é uma coleção de objetos. Os conjuntos são indicados com letras maiúsculas A, B, C, X, … e os elementos de um conjunto são indicados com letras minúsculas a, b, c, x, etc. Quando um elemento a pertence a um conjunto X, é indicado por:

Quando não pertence ao X, a notação é:

A maneira de representar os conjuntos é colocando seus elementos dentro das teclas. Por exemplo, o conjunto de números naturais é representado por:

Os conjuntos também podem ser representados sem escrever uma lista explícita de seus elementos. Eles podem ser expressos no formato {:}. Os dois pontos são lidos “de modo que”. Uma variável que representa os elementos do conjunto é colocada à esquerda dos dois pontos e a propriedade ou condição que eles satisfazem é colocada no lado direito. Isto é:

Por exemplo, o conjunto de números inteiros maiores que -4 pode ser expresso como:

Ou equivalente e mais abreviado, como:

Da mesma forma, as seguintes expressões representam os conjuntos de números ímpares e pares, respectivamente:

União, interseção e complementos de conjunto
A seguir, veremos os análogos dos conectivos lógicos no caso de conjuntos, que fazem parte das operações básicas entre conjuntos.
União e interseção
A união e interseção de conjuntos são definidas, respectivamente, da seguinte forma:

Por exemplo, considere os conjuntos:

Então, você precisa:

Complemento
O complemento de um conjunto é formado pelos elementos que não pertencem ao referido conjunto (do mesmo tipo que o original representa). O complemento de um conjunto A é indicado por:

Por exemplo, dentro de números naturais, o complemento do conjunto de números pares é o de números ímpares e vice-versa.
Para determinar o complemento de um conjunto, o conjunto universal ou principal dos elementos considerados deve estar claro desde o início. Por exemplo, não é o mesmo considerar o complemento de um conjunto de números naturais do que números racionais.
A tabela a seguir mostra o relacionamento ou analogia existente entre as operações em conjuntos definidos anteriormente e os conectivos da lógica proposicional:
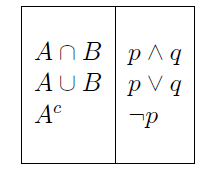
Leis de Morgan para conjuntos
Finalmente, as leis de Morgan sobre conjuntos são:
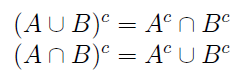
Em palavras: o complemento de uma união é a interseção dos complementos, e o complemento de uma interseção é a união dos complementos.
Uma demonstração matemática da primeira igualdade seria a seguinte:

A demonstração do segundo é análoga.
Referências
- Almaguer, G. (2002). Matemática 1. Editorial Limusa.
- Aylwin, CU (2011). Lógica, Conjuntos e Números. Mérida – Venezuela: Conselho de Publicações, Universidade de Los Andes.
- Barrantes, H., Díaz, P., Murillo, M. e Soto, A. (1998). Introdução à Teoria dos Números. EUNED
- Castañeda, S. (2016). Curso básico de teoria dos números. Universidade do Norte
- Cofré, A. & Tapia, L. (1995). Como desenvolver o raciocínio lógico matemático. Publicação Universitária.
- Guevara, MH (sf). Teoria dos Números. EUNED
- Saragoça, AC (sf). Teoria dos números. Editorial Vision Books.