O movimento do pêndulo é um fenômeno físico que pode ser observado em diversos contextos, desde um relógio de parede até em experimentos científicos. O pêndulo simples é um tipo específico de pêndulo que se movimenta de forma harmônica e regular, seguindo as leis da física do movimento harmônico simples. Neste tipo de movimento, a aceleração do pêndulo é proporcional e oposta ao seu deslocamento, resultando em um movimento periódico de vai e vem. O estudo do pêndulo simples é fundamental para compreender os princípios da dinâmica e da cinemática.
Entendendo o movimento de um pêndulo e suas características físicas e matemáticas.
Quando observamos o movimento de um pêndulo, podemos perceber que ele descreve um padrão repetitivo de vai e vem. Esse movimento é conhecido como pêndulo simples e pode ser descrito matematicamente como um movimento harmônico simples.
Um pêndulo simples é composto por uma massa suspensacorda inextensível
Para descrever o movimento do pêndulo matematicamente, podemos utilizar a equação do movimento harmônico simples, que é dada por:
T = 2π√(l/g)
Onde T é o período de oscilação do pêndulo, l é o comprimento da corda e g é a aceleração devido à gravidade. Essa equação nos permite prever o período de oscilação do pêndulo com base em suas características físicas.
Ao entender as características físicas e matemáticas envolvidas, podemos prever e analisar o comportamento desse sistema de forma precisa.
Definição e características do movimento harmônico simples: descubra tudo sobre esse fenômeno físico.
O movimento harmônico simples é um fenômeno físico que ocorre quando um sistema oscila em torno de um ponto de equilíbrio, seguindo uma trajetória periódica. Esse tipo de movimento é caracterizado por ser repetitivo, senoidal e isocrônico.
No movimento harmônico simples, a força que atua sobre o sistema é diretamente proporcional à sua distância em relação ao ponto de equilíbrio e tem sentido contrário ao deslocamento. Essa força é conhecida como força restauradora, responsável por trazer o sistema de volta ao equilíbrio quando perturbado.
As principais características do movimento harmônico simples incluem a amplitude da oscilação, que é a máxima distância percorrida pelo sistema em relação ao ponto de equilíbrio, e o período da oscilação, que é o tempo necessário para que o sistema complete um ciclo completo.
O pêndulo simples é um exemplo clássico de movimento harmônico simples, onde um objeto de massa é suspenso por um fio inextensível e de massa desprezível. O período de oscilação de um pêndulo simples depende do comprimento do fio e da aceleração da gravidade.
O pêndulo simples é um exemplo prático desse tipo de movimento, onde a força restauradora é a gravidade e o período de oscilação depende do comprimento do fio e da aceleração da gravidade.
Funcionamento do pêndulo simples: entenda o movimento oscilatório e suas características principais.
O pêndulo simples é um sistema físico que consiste em uma massa presa a uma haste fixa por um ponto de articulação. Quando o pêndulo é afastado de sua posição de equilíbrio e solto, ele realiza um movimento oscilatório ao redor desse ponto.
Este movimento é conhecido como movimento harmônico simples, pois a aceleração do pêndulo é diretamente proporcional e oposta ao seu deslocamento em relação à posição de equilíbrio. Ou seja, quanto mais longe o pêndulo estiver de sua posição de equilíbrio, maior será a força restauradora que o trará de volta.
Uma das características principais do pêndulo simples é o seu período, que é o tempo que o pêndulo leva para realizar uma oscilação completa. O período do pêndulo simples é influenciado pelo comprimento da haste e pela aceleração da gravidade.
Além disso, a amplitude do movimento do pêndulo simples é o máximo deslocamento que a massa realiza em relação à posição de equilíbrio. Quanto maior a amplitude, maior será a velocidade máxima atingida pela massa durante o movimento.
Suas características principais incluem o período, a amplitude e a influência do comprimento da haste e da aceleração da gravidade em seu comportamento.
Diferenças entre pêndulo simples e físico: entenda as características de cada um.
O movimento do pêndulo é um fenômeno físico que pode ser estudado através de dois tipos principais: o pêndulo simples e o pêndulo físico. As principais diferenças entre eles estão relacionadas às suas características e propriedades.
O pêndulo simples é composto por um fio inextensível e sem massa, no qual está preso uma massa pontual. Ele oscila em um plano vertical sob a ação da gravidade, sem sofrer influência de forças externas. O movimento do pêndulo simples é descrito como um movimento harmônico simples, ou seja, um movimento periódico e regular.
Por outro lado, o pêndulo físico é composto por um objeto com dimensões não desprezíveis, o que significa que sua massa não está concentrada em um único ponto. Isso resulta em um movimento mais complexo, com diferentes momentos de inércia e uma trajetória não necessariamente linear.
Enquanto o pêndulo simples é utilizado em estudos teóricos e experimentos básicos, o pêndulo físico é empregado em aplicações mais práticas e reais, como na medição de grandezas físicas e na construção de instrumentos de precisão.
Ambos são importantes para o estudo da física e possuem aplicações distintas em diversos campos do conhecimento.
Movimento do pêndulo: pêndulo simples, harmônico simples
Um pêndulo é um objeto (idealmente uma massa pontual) pendurado por um fio (idealmente sem massa) de um ponto fixo e que oscila graças à força da gravidade, essa força invisível misteriosa que, entre outras coisas, mantém o universo colado.
O movimento pendular é aquele que ocorre em um objeto de um lado para outro, pendurado em uma fibra, cabo ou fio. As forças envolvidas nesse movimento são a combinação da força da gravidade (vertical, em direção ao centro da Terra) e a tensão da linha (direção da linha).
É o que os relógios de pêndulo fazem (daí o nome) ou os balanços dos playgrounds das crianças.Em um pêndulo ideal, o movimento oscilatório continuaria perpetuamente. Em um pêndulo real, por outro lado, o movimento acaba parando com o tempo devido ao atrito com o ar.
Pensar em um pêndulo torna inevitável evocar a imagem do relógio de pêndulo, a memória daquele relógio antigo e imponente na casa de campo dos avós. Ou talvez a história de horror de Edgar Allan Poe, O poço e o pêndulo cuja narração é inspirada por um dos muitos métodos de tortura usados pela Inquisição Espanhola.
A verdade é que diferentes tipos de pêndulos têm aplicações variadas além da medição do tempo, como, por exemplo, determinar a aceleração da gravidade em um determinado local e até demonstrar a rotação da Terra, como fez o físico francês Jean Bernard Léon Foucault
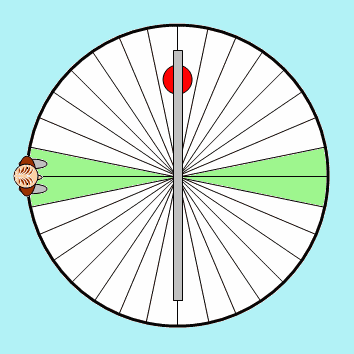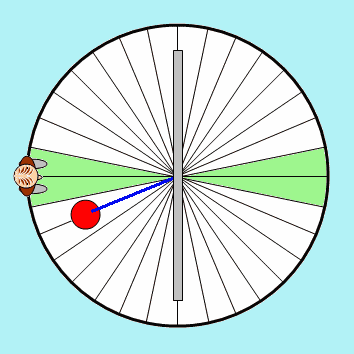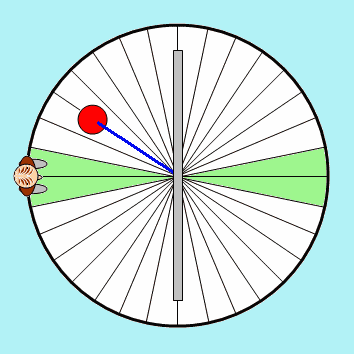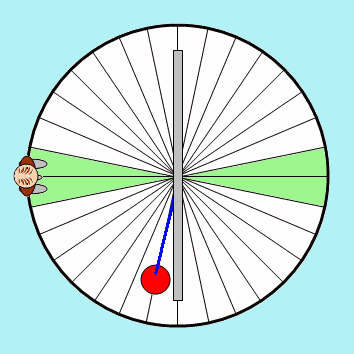
O pêndulo simples e o movimento vibratório harmônico simples
Pêndulo simples
O pêndulo simples, embora seja um sistema ideal, permite uma abordagem teórica do movimento de um pêndulo.
Embora as equações do movimento de um pêndulo simples possam ser um pouco complexas, a verdade é que, quando a amplitude ( A ), ou deslocamento da posição de equilíbrio, do movimento é pequena, ela pode ser aproximada com as equações de um movimento harmônico Simples que eles não são excessivamente complicados.
Movimento harmônico simples
O movimento harmônico simples é um movimento periódico, ou seja, repetido ao longo do tempo. Além disso, é um movimento oscilatório cuja oscilação ocorre em torno de um ponto de equilíbrio, ou seja, um ponto no qual o resultado líquido da soma das forças aplicadas ao corpo é zero.
Assim, uma característica fundamental do movimento pendular é seu período ( T ), que determina o tempo necessário para concluir um ciclo completo (ou oscilação completa). O período de um pêndulo é determinado pela seguinte expressão:

sendo, l = o comprimento do pêndulo; e g = o valor da aceleração da gravidade.
Uma magnitude relacionada ao período é a frequência ( f ), que determina o número de ciclos que o pêndulo viaja em um segundo. Dessa maneira, a frequência pode ser determinada a partir do período com a seguinte expressão:
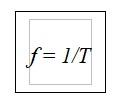
Dinâmica do movimento pendular
As forças envolvidas no movimento são o peso, ou o que é o mesmo, a força da gravidade ( P ) e a tensão do fio ( T ). A combinação dessas duas forças é o que causa o movimento.
Enquanto a tensão é sempre direcionada na direção do fio ou corda que une a massa ao ponto fixo e, portanto, não é necessário quebrá-la; o peso é sempre direcionado verticalmente para o centro de massa da Terra e, portanto, é necessário decompô-lo em seus componentes tangenciais e normais ou radiais.

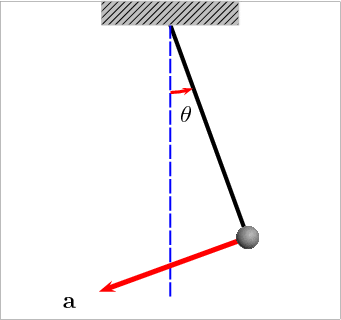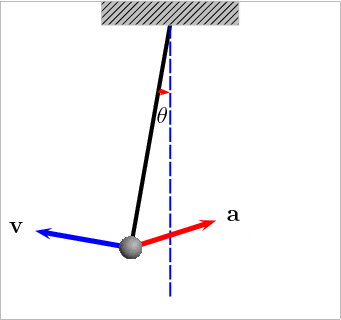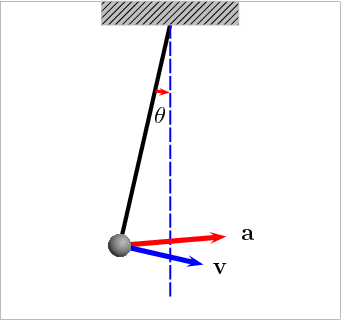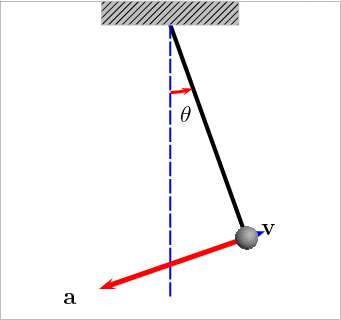
A componente tangencial do peso P t = mg sin θ , enquanto que a componente normal do peso é P N = mg cos θ . Este segundo é compensado com a tensão da linha; sendo, portanto, em última análise, responsável pelo movimento o componente tangencial do peso que atua como uma força de recuperação.
Deslocamento, velocidade e aceleração
O deslocamento de um movimento harmônico simples e, portanto, do pêndulo, é determinado pela seguinte equação:
x = A ω cos (ω t + θ 0 )
onde ω = é a velocidade angular de rotação; t = é a hora; e θ 0 = é a fase inicial.
Dessa forma, essa equação permite determinar a posição do pêndulo a qualquer momento. Nesse sentido, é interessante destacar algumas relações entre algumas das magnitudes do simples movimento harmônico.
ω = 2 ∏ / T = 2 ∏ / f
Por outro lado, a fórmula que governa a velocidade do pêndulo em função do tempo é obtida derivando o deslocamento em função do tempo, assim:
v = dx / dt = -A ω sen ( ω t + θ 0 )
Procedendo da mesma maneira, obtém-se a expressão da aceleração em relação ao tempo:
a = dv / dt = – A ω 2 cos ( ω t + θ 0 )
Velocidade e aceleração
Observando tanto a expressão da velocidade quanto a da aceleração, alguns aspectos interessantes do movimento pendular são apreciados.
A velocidade assume seu valor máximo na posição de equilíbrio, momento em que a aceleração é zero, pois, como já foi dito acima, naquele momento a força líquida é zero.
Pelo contrário, nos extremos do deslocamento ocorre o oposto; aí a aceleração assume o valor máximo e a velocidade assume um valor nulo.
A partir das equações de velocidade e aceleração, é fácil deduzir o módulo de velocidade máxima e o módulo de aceleração máxima. Simplesmente pegue o valor máximo possível para sen (ω t + θ 0 ) e cos (ω t + θ 0 ), que em ambos os casos é 1.
│ v max │ = A ω
│ a max │ = A ω 2
O momento em que o pêndulo atinge a velocidade máxima é quando passa pelo ponto de equilíbrio de forças desde então sen (ω t + θ 0 ) = 1 . Pelo contrário, a aceleração máxima é alcançada em ambas as extremidades do movimento desde então cos (ω t + θ 0 ) = 1
Conclusão
Um pêndulo é um objeto fácil de projetar e aparente com um simples movimento, embora a verdade seja que, no fundo, é muito mais complexo do que parece.
No entanto, quando a amplitude inicial é pequena, seu movimento pode ser explicado com equações que não são excessivamente complicadas, pois pode ser aproximado com as equações do movimento vibratório harmônico simples.
Os diferentes tipos de pêndulos existentes têm diferentes aplicações para a vida cotidiana e no campo científico.
Referências
- Van Baak, Tom (novembro de 2013).«Uma nova e maravilhosa equação do período do pêndulo». Boletim de Ciências Horológicas.2013 (5): 22-30.
- Pêndulo (nd) Na Wikipedia Recuperado em 7 de março de 2018, em en.wikipedia.org.
- Pêndulo (matemática) . (nd) Na Wikipedia Recuperado em 7 de março de 2018, em en.wikipedia.org.
- Llorente, Juan Antonio (1826).A história da Inquisição da Espanha. Resumido e traduzido por George B. Whittaker . Universidade de Oxford pp.XX, prefácio.
- Poe, Edgar Allan (1842).O poço e o pêndulo . Booklassic ISBN 9635271905.