O gravicentro, também conhecido como centro de gravidade, é o ponto em um objeto onde toda a massa se concentra e as forças de gravidade atuam. Esse ponto é importante para determinar o equilíbrio de um objeto e sua estabilidade.
Por exemplo, em um triângulo equilátero, o gravicentro está localizado no ponto de interseção das medianas, que são segmentos de reta que ligam o vértice de um triângulo ao ponto médio do lado oposto. Em um objeto simétrico, o gravicentro estará localizado no centro geométrico do objeto.
Conhecer o gravicentro de um objeto é essencial para projetar estruturas estáveis, como pontes, edifícios e veículos, garantindo que estejam devidamente equilibrados e seguros.
Qual a utilidade do baricentro na geometria e física?
O baricentro é um conceito fundamental na geometria e na física, sendo de extrema importância para a compreensão de diversos fenômenos e cálculos de equilíbrio. O baricentro, também conhecido como centro de massa, é o ponto onde se concentra a massa de um corpo de forma equilibrada, sendo o ponto de equilíbrio de um sistema.
Na geometria, o baricentro é utilizado para determinar o centro de gravidade de figuras geométricas complexas, como triângulos, quadriláteros e polígonos em geral. Ele é calculado a partir das coordenadas dos vértices da figura, sendo de grande importância em aplicações práticas como a engenharia civil, por exemplo.
Na física, o baricentro é fundamental para a análise de sistemas de partículas e corpos extensos. Ele é utilizado para determinar o ponto de aplicação da força resultante em um sistema, facilitando o estudo de movimentos e equilíbrios. Além disso, o baricentro é essencial para a resolução de problemas de mecânica, como momento de inércia e torque.
Um exemplo prático de aplicação do baricentro é o caso de um triângulo equilátero, onde o baricentro coincide com o centro da circunferência circunscrita ao triângulo. Isso significa que o baricentro está equidistante dos três vértices do triângulo, representando o ponto de equilíbrio das massas distribuídas.
Em resumo, o baricentro é uma ferramenta poderosa na geometria e na física, sendo essencial para a análise de sistemas complexos e o cálculo de equilíbrios. Compreender o conceito de baricentro é fundamental para o estudo dessas áreas do conhecimento, tornando-se uma peça-chave em diversos contextos práticos e teóricos.
Métodos para determinar o centro de um triângulo de forma precisa e eficaz.
Para determinar o centro de um triângulo de forma precisa e eficaz, existem diversos métodos que podem ser utilizados. Um desses métodos é o cálculo do gravicentro, também conhecido como centro de gravidade ou baricentro do triângulo.
O gravicentro de um triângulo é o ponto de interseção das três medianas do triângulo, que são segmentos de reta que ligam cada vértice do triângulo ao ponto médio do lado oposto. Para encontrar o gravicentro, basta calcular as coordenadas médias dos vértices do triângulo e então traçar as medianas até encontrar o ponto de interseção.
Outro método para determinar o centro de um triângulo é o cálculo do circuncentro, que é o centro da circunferência circunscrita ao triângulo. O circuncentro é o ponto de interseção das bissetrizes dos ângulos do triângulo. Para encontrá-lo, basta traçar as bissetrizes dos ângulos do triângulo até encontrar o ponto de interseção.
Além disso, o incentro é outro centro importante de um triângulo, sendo o ponto de interseção das três bissetrizes internas do triângulo. O incentro é o centro da circunferência inscrita no triângulo, que tangencia os três lados do triângulo. Para encontrá-lo, basta traçar as bissetrizes internas até encontrar o ponto de interseção.
Em resumo, existem diferentes métodos para determinar o centro de um triângulo de forma precisa e eficaz, como o cálculo do gravicentro, circuncentro e incentro. Cada um desses centros possui propriedades únicas que podem ser exploradas em diversos contextos matemáticos e geométricos.
Como determinar o ponto de equilíbrio de uma figura geométrica qualquer?
Para determinar o ponto de equilíbrio de uma figura geométrica qualquer, é necessário encontrar o seu gravicentro, também conhecido como centro de gravidade. O gravicentro é o ponto onde se concentra toda a massa da figura, de forma que se ela for suspensa por esse ponto, ficará em equilíbrio.
Para calcular o gravicentro de uma figura geométrica, é preciso levar em consideração a distribuição de massa da figura. Em figuras simétricas, o gravicentro estará no ponto de simetria. Já em figuras irregulares, é necessário utilizar fórmulas específicas para encontrar o ponto de equilíbrio.
Um exemplo simples é o caso de um triângulo equilátero. O gravicentro desse triângulo está localizado no ponto de encontro das suas medianas, que são segmentos de reta que ligam um vértice ao ponto médio do lado oposto. Nesse caso, o gravicentro divide cada mediana em duas partes, sendo a parte mais próxima do vértice equivalente a dois terços da mediana.
Portanto, encontrar o ponto de equilíbrio de uma figura geométrica qualquer envolve calcular o seu gravicentro, levando em consideração a distribuição de massa da figura e utilizando fórmulas específicas conforme a sua forma. Uma vez encontrado o gravicentro, é possível determinar o ponto de equilíbrio da figura.
Entendendo a definição e cálculo da área de um triângulo de forma simples.
Para entender a definição e cálculo da área de um triângulo de forma simples, precisamos lembrar que a área de um triângulo é dada pela fórmula A = (base x altura) / 2. A base do triângulo é o lado mais longo, e a altura é a distância perpendicular da base ao vértice oposto.
Agora, vamos falar sobre o Gravicentro. O Gravicentro, também conhecido como centro de gravidade ou baricentro, é o ponto de interseção das medianas de um triângulo. As medianas são segmentos de reta que ligam um vértice ao ponto médio do lado oposto. O Gravicentro é o ponto onde o triângulo equilátero pode ser equilibrado.
Para encontrar o Gravicentro de um triângulo, basta traçar as medianas e identificar o ponto de interseção. Por exemplo, no triângulo ABC, as medianas se cruzam no ponto G, que é o Gravicentro.
Em resumo, a área de um triângulo pode ser calculada pela fórmula A = (base x altura) / 2, enquanto o Gravicentro é o ponto de interseção das medianas de um triângulo.
O que é o Gravicentro? (com exemplos)
O gravicentro é uma definição amplamente usada em geometria ao trabalhar com triângulos.
Para entender a definição de gravicentro, primeiro é necessário conhecer a definição de “medianas” de um triângulo.

As medianas de um triângulo são os segmentos de linha que começam em cada vértice e atingem o ponto médio do lado oposto desse vértice.
O ponto de interseção das três medianas de um triângulo é chamado de baricentro ou também é conhecido como gravicentro.
Não basta apenas conhecer a definição, é interessante saber como esse ponto é calculado.
Cálculo do Baricenter
Dado um triângulo ABC com vértices A = (x1, y1), B = (x2, y2) e C = (x3, y3), o gravicentro é a interseção das três medianas do triângulo.
Uma fórmula rápida que permite o cálculo do gravicentro de um triângulo, sendo conhecidas as coordenadas de seus vértices:
G = ((x1 + x2 + x3) / 3, (y1 + y2 + y3) / 3).
Com esta fórmula, você pode conhecer a localização do gravicentro no plano cartesiano.
Características do Gravicentro
Não é necessário desenhar as três medianas do triângulo, porque ao desenhar duas delas será evidente onde está o gravicentro.

O gravicentro divide cada mediana em 2 partes cuja proporção é de 2: 1, ou seja, os dois segmentos de cada mediana são divididos em segmentos de comprimentos 2/3 e 1/3 do comprimento total, sendo a distância maior do que existe. entre o vértice e o gravicentro.
A imagem a seguir ilustra melhor essa propriedade.

A fórmula para o cálculo do gravicentro é muito simples de aplicar. A maneira de obter essa fórmula é calcular as equações da linha que definem cada mediana e, em seguida, encontrar o ponto de corte dessas linhas.
Exercícios
Abaixo está uma pequena lista de problemas com o cálculo do baricentro.
1.- Dado um triângulo dos vértices A = (0,0), B = (1,0) e C = (1,1), calcule o gravicentro do referido triângulo.
Usando a fórmula dada, pode-se concluir rapidamente que o gravicentro do triângulo ABC é:
G = ((0 + 1 + 1) / 3, (0 + 0 + 1) / 3) = (2/3, 1/3).
2.- Se um triângulo possui vértices A = (0,0), B = (1,0) e C = (1 / 2,1), quais são as coordenadas do gravicentro?
Como os vértices do triângulo são conhecidos, a fórmula para o cálculo do gravicentro é aplicada. Portanto, o gravicentro possui coordenadas:
G = ((0 + 1 + 1/2) / 3, (0 + 0 + 1) / 3) = (1/2, 1/3).
3.- Calcule os possíveis gravicentros para um triângulo equilátero, de modo que dois de seus vértices sejam A = (0,0) e B = (2,0).
Neste exercício, apenas dois vértices do triângulo estão sendo especificados. Para encontrar os possíveis gravicentros, o terceiro vértice do triângulo deve primeiro ser calculado.
Como o triângulo é equilátero e a distância entre A e B é 2, o terceiro vértice C deve estar, deve estar à distância 2 de A e B.
Usando o fato de que em um triângulo equilátero a altura coincide com a mediana e também usando o teorema de Pitágoras, pode-se concluir que as opções para as coordenadas do terceiro vértice são C1 = (1, √3) ou C2 = (1, – √3).

Portanto, as coordenadas dos dois possíveis gravicentros são:
G1 = ((0 + 2 + 1) / 3, (0 + 0 + √3) / 3) = (3/3, √3 / 3) = (1, √3 / 3),
G2 = ((0 + 2 + 1) / 3, (0 + 0-√3) / 3) = (3/3, -√3 / 3) = (1, -√3 / 3).
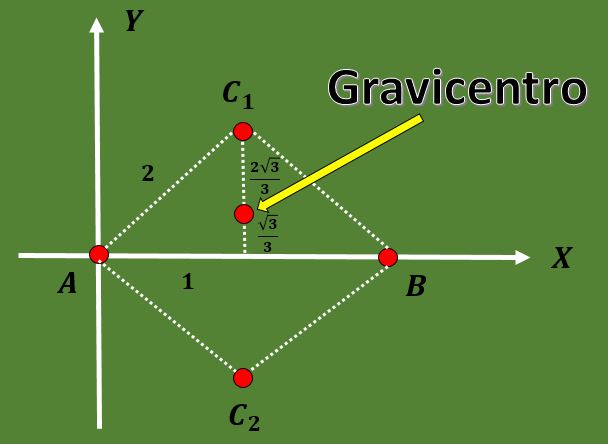
Graças às contas anteriores, também é possível notar que a mediana foi dividida em duas partes cuja proporção é 2: 1.
Referências
- Landaverde, F. d. (1997). Geometria (Reimpressão ed.). Progresso
- Leake, D. (2006). Triângulos (ilustração ilustrada). Heinemann-Raintree.
- Pérez, CD (2006). Pré-cálculo Pearson Education.
- Ruiz, Á .; Barrantes, H. (2006). Geometrias Tecnologia CR.
- Sullivan, M. (1997). Pré-cálculo Pearson Education.
- Sullivan, M. (1997). Trigonometria e Geometria Analítica. Pearson Education.