As razões trigonométricas são ferramentas matemáticas fundamentais para o estudo da geometria e da trigonometria. Elas são utilizadas para relacionar os ângulos de um triângulo retângulo com os comprimentos de seus lados. Neste texto, exploraremos exemplos práticos de como calcular as razões trigonométricas seno, cosseno e tangente, além de apresentar exercícios para fixação do conteúdo e algumas aplicações dessas razões em situações do cotidiano e em diversas áreas da ciência e tecnologia.
Entendendo a trigonometria: definição e exemplos práticos de aplicação no cotidiano.
Trigonometria é a parte da matemática que estuda as relações entre os ângulos e os lados de um triângulo. Ela é fundamental para a resolução de problemas que envolvem medidas de ângulos e distâncias, sendo amplamente aplicada em diversas áreas, como engenharia, arquitetura, física e astronomia.
As razões trigonométricas são funções matemáticas que relacionam os ângulos de um triângulo com as medidas de seus lados. As principais razões trigonométricas são o seno, cosseno e tangente, representadas pelas letras sen, cos e tan, respectivamente.
Para entender melhor as razões trigonométricas, podemos utilizar exemplos práticos de aplicação no cotidiano. Por exemplo, ao construir uma ponte, os engenheiros precisam calcular as medidas dos ângulos para garantir a estabilidade da estrutura. Nesse caso, a trigonometria é essencial para determinar as dimensões corretas dos pilares e vigas.
Outro exemplo de aplicação da trigonometria no dia a dia é na navegação marítima. Os navegadores utilizam as razões trigonométricas para determinar a posição de um navio em alto mar, considerando a direção do vento e a velocidade da embarcação.
Para praticar as razões trigonométricas, é possível resolver exercícios que envolvem o cálculo de ângulos e lados em triângulos retângulos. Esses exercícios ajudam a compreender melhor as relações trigonométricas e a aplicá-las em situações reais.
Ao compreender as razões trigonométricas e suas aplicações no cotidiano, é possível utilizar esse conhecimento de forma prática e eficiente em diversas situações do dia a dia.
Usos práticos da trigonometria: onde ela é aplicada e como beneficia diversas áreas.
A trigonometria é uma área da matemática que estuda as relações entre os ângulos e os lados de um triângulo. Suas razões trigonométricas, como seno, cosseno e tangente, têm uma ampla gama de aplicações práticas em diversas áreas, beneficiando desde a engenharia até a física e a astronomia.
Um dos usos mais comuns da trigonometria é na resolução de problemas de navegação. Por exemplo, ao usar a trigonometria, é possível determinar a posição de um navio no mar com base em observações de faróis ou estrelas. Isso é fundamental para a navegação marítima e a aviação, garantindo a segurança das viagens.
Na engenharia civil, a trigonometria é essencial para o cálculo de estruturas, como pontes e edifícios. Os engenheiros utilizam as razões trigonométricas para determinar a altura de um prédio, a inclinação de uma rampa ou a extensão de um cabo de aço, garantindo a estabilidade e segurança das construções.
Além disso, a trigonometria é aplicada na física para analisar movimentos oscilatórios, como o movimento de uma onda, ou calcular a trajetória de um projétil. Em astronomia, as razões trigonométricas são utilizadas para determinar a posição dos astros no céu e prever eclipses e fenômenos astronômicos.
Seja na navegação, na engenharia, na física ou na astronomia, as razões trigonométricas são indispensáveis para o avanço da ciência e da tecnologia.
Aplicações práticas das relações trigonométricas no dia a dia.
As relações trigonométricas são fundamentais não apenas na matemática, mas também possuem diversas aplicações práticas no nosso dia a dia. Um exemplo comum é a utilização da trigonometria na construção civil, onde os profissionais precisam calcular ângulos e distâncias para garantir a precisão das estruturas que estão sendo construídas.
Outra aplicação importante das relações trigonométricas é na navegação marítima e aérea. Os pilotos e navegadores utilizam esses conceitos para determinar a posição de suas embarcações e aeronaves, levando em consideração ângulos, distâncias e velocidades. Esses cálculos são essenciais para garantir a segurança dos passageiros e tripulantes.
No campo da engenharia, as relações trigonométricas são utilizadas para projetar pontes, torres, viadutos e outras estruturas, levando em conta os ângulos de inclinação, a altura e a distância entre os pontos de apoio. Esses cálculos garantem a estabilidade e a segurança das construções.
Além disso, a trigonometria também é aplicada em áreas como a astronomia, a geografia, a física e até mesmo em jogos de computador, onde os desenvolvedores utilizam esses conceitos para criar gráficos e animações realistas. Portanto, as relações trigonométricas têm um papel fundamental em diversas áreas do conhecimento e do cotidiano.
Desde a construção de edifícios até a navegação marítima, a trigonometria está presente em diversos aspectos do nosso dia a dia, contribuindo para a precisão, a segurança e o desenvolvimento de diversas áreas profissionais.
Guia para escolher a razão trigonométrica correta em situações específicas.
Quando se trata de escolher a razão trigonométrica correta em situações específicas, é importante ter em mente algumas dicas úteis que podem facilitar o processo. A escolha da razão trigonométrica correta depende do ângulo envolvido e das informações disponíveis no problema.
Senhoras vezes, pode ser necessário usar a razão seno quando estamos lidando com a hipotenusa e o cateto oposto de um triângulo retângulo. Por outro lado, se estivermos trabalhando com o cateto adjacente e a hipotenusa, a razão cosseno pode ser mais apropriada.
É importante lembrar que a tangente é a razão entre o cateto oposto e o cateto adjacente de um triângulo retângulo. Portanto, se precisarmos comparar esses dois lados do triângulo, a tangente é a razão trigonométrica a ser utilizada.
Para situações em que temos o raio de um círculo trigonométrico e precisamos encontrar a coordenada y de um ponto na circunferência, a razão seno é a mais apropriada. Por outro lado, se precisarmos encontrar a coordenada x, a razão cosseno deve ser utilizada.
Lembrando dessas dicas simples, podemos escolher a razão trigonométrica correta de forma mais eficiente e precisa em diversas situações. Praticar com exemplos e exercícios pode ajudar a solidificar esses conceitos e tornar mais fácil a aplicação das razões trigonométricas em problemas do cotidiano.
Razões trigonométricas: exemplos, exercícios e aplicações
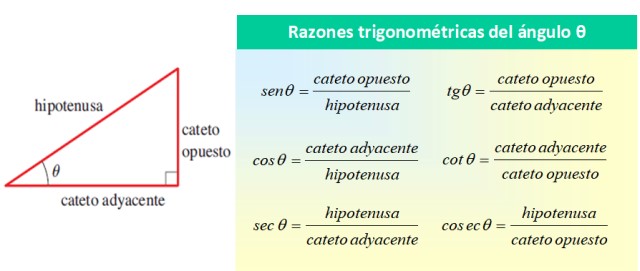
As razões trigonométricas são razões ou razões relacionadas ao valor dos lados de um triângulo retângulo. Estes lados são: duas pernas que formam 90º entre si e a hipotenusa, que forma o ângulo agudo θ com uma das pernas.
Podem ser formadas 6 proporções. Seus nomes e respectivas abreviações são:
- seio
- cosseno (cos)
- tangente (tg ou castanho)
- cotangente (ctg ou cotan)
- secante (seg) e
- cossecante (cossec)
Todos eles se referiram ao ângulo θ, como mostra a figura a seguir:
As razões trigonométricas básicas do ângulo θ são sin θ, cos θ e tan θ, enquanto as relações restantes podem ser expressas em termos desses três. Da tabela anterior, pode-se ver que:
- sec θ = 1 / cos θ
- cosec θ = 1 / sin θ
- cot θ = 1 / tg θ
O tamanho dos lados do triângulo não influencia o valor das proporções, pois dois triângulos cujos ângulos medem o mesmo são triângulos semelhantes e os respectivos quocientes entre os lados têm o mesmo valor.
Exemplo
Por exemplo, vamos calcular as proporções trigonométricas do ângulo θ nos seguintes triângulos:
Para o triângulo pequeno, temos as três razões básicas do ângulo θ:
sin θ = 3/5
cos θ = 4/5
tg θ = ¾
E agora vamos calcular as três razões básicas de θ com o triângulo grande:
sen θ = 30/50 = 3/5
cos θ = 40/50 = 4/5
tg θ = 30/40 = ¾
Um detalhe importante a ser levado em consideração é o seguinte: o pecado θ e o cos θ são menores que 1, pois as pernas sempre medem menos que a hipotenusa. Em efeito:
sen θ = 3/5 = 0,6
cos θ = 4/5 = 0,8
Exercícios resolvidos
Nos exercícios a seguir, você deve resolver o triângulo retângulo, o que significa encontrar o comprimento de seus três lados e a medida de seus ângulos internos, um dos quais sempre mede 90º.
O teorema de Pitágoras se aplica a triângulos retângulos e é muito útil quando dois lados são conhecidos e a falta deve ser determinada. O teorema diz assim:
Hipotenusa 2 = perna oposta 2 + perna adjacente 2
Podemos verificar o teorema de Pitágoras com o pequeno triângulo da figura 2, cujas pernas são 3 e 4. A ordem pela qual as pernas são tomadas não importa. Aplicando o teorema, temos:
Hipotenusa 2 = 3 2 + 4 2 = 9 + 16 = 25
Portanto, a hipotenusa é:
Hipotenusa = √25 = 5
– Exercício 1
Calcule as relações trigonométricas dos ângulos mostrados nos seguintes triângulos:
Solução para
Esse triângulo é o mesmo da figura 3, mas pedimos as razões trigonométricas do outro ângulo agudo, denotado α. A afirmação não oferece o valor da hipotenusa, no entanto, pela aplicação do teorema de Pitágoras, sabemos que vale 5.
As proporções podem ser calculadas diretamente a partir da definição, tomando cuidado ao selecionar a perna que é o oposto do ângulo α para calcular o pecado α. Vamos ver:
- sin α = 4/5
- cos α = 3/5
- tg α = 4/3
- berço α = ¾
- sec α = 1 / (3/5) = 5/3
- cosec α = 1 / (4/5) = 5/4
E, como podemos ver, os valores das taxas trigonométricas foram trocados. De fato, α e θ são ângulos complementares, o que significa que somam 90º. Nesse caso, é verdade que sin α = cos θ e assim por diante para as outras razões.
Solução b
Vamos calcular a hipotenusa do triângulo usando o teorema de Pitágoras:
Hipotenusa 2 = 20 2 + 21 2 = 841
√841 = 29
Portanto, as 6 razões trigonométricas do ângulo β são:
- sin β = 20/29
- cos β = 21/29
- tg β = 20/21
- berço β = 21/20
- sec β = 1 / (21/29) = 29/21
- cosec β = 1 / (20/29) = 20/29
– Exercício 2
a) Encontre o valor de x na figura.
b) Calcule o perímetro dos 3 triângulos mostrados.
Solução para
Na figura, podemos identificar vários triângulos, em particular o triângulo direito à esquerda, que tem uma perna igual a 85 e o ângulo agudo de 60º.
Com as informações deste triângulo, podemos calcular o lado b. Não é a medida solicitada pela declaração, mas conhecer seu valor é uma etapa anterior.
Para determinar, a razão apropriada é tg 60 º = 85 / b, uma vez que b é a perna adjacente a 60 º e 85 é o oposto do referido ângulo. Portanto:
b = 85 / tg 60º = 85 / √3
Uma vez que b é conhecido, usaremos o grande triângulo externo externo, que tem um lado comum com o triângulo anterior: o que mede 85. Essa é a perna oposta ao ângulo de 30º.
De Ali:
30º perna adjacente = (85 / √3) + x
Agora podemos levantar o seguinte:
85 / [(85 / √3) + x] = tg 30º
O que está entre colchetes multiplica o tg 30º:
85 = [(85 / √3) + x]. tg 30º
Aplicando a propriedade distributiva da multiplicação:
85 = tg 30º. (85 / √3) + x. tg 30º
Portanto:
x.tg 30º = 85 – tg 30º. (85 / √3) = 85 [1 – tg 30º. (1 / √3)] = 85. (2/3) = 170/3
Substituindo o valor tg 30º = √3 / 3:
x = (170/3) ÷ (√3 / 3) = 98,15
Solução b
Perímetro pequeno triângulo
Seja h 1 a hipotenusa deste triângulo, que pode ser calculada pelo teorema de Pitágoras ou por uma razão trigonométrica, por exemplo cos 60º:
cos 60º = 85 / √3 / h 1 → h 1 = (85 / √3) ÷ cos 60º = 98,1
Para encontrar P, o perímetro deste triângulo, basta adicionar os 3 lados:
P = 85 + (85 / √3) + 98,1 = 232,2
Perímetro do triângulo externo
Seja h 2 a hipotenusa do triângulo externo:
sen 30º = 85 2 h 2
h 2 = 85 ÷ sen 30º = 170
Para este triângulo, o perímetro é:
P = 85 + [(85 / √3) + 98,15] + 170 = 402,22
Perímetro do triângulo não direito
Já conhecemos todos os lados deste triângulo:
P = x + h 1 + h 2 = 98,15 + 98,15 + 170 = 366,3
Aplicações de razões trigonométricas
Razões trigonométricas têm muitas aplicações práticas, por exemplo, alturas podem ser calculadas.
Suponha que uma torre de água esteja a 200 metros de um edifício. Um observador em uma janela observa que o ângulo de elevação da extremidade superior da torre é de 39º, enquanto o ângulo de depressão no qual a base da torre é vista é de 25º. Ele pergunta:
a) Qual é a altura da torre?
b) Qual é a altura da janela?
Solução para
Da perna oposta até 39º do triângulo superior, obtemos uma parte da resposta:
h 1 /325 = tg 39º → h 1 = 325. tg 39º pés = 263,2 pés
De maneira semelhante, obtemos o restante da altura da torre, chamada h 2, do triângulo inferior:
h 2 /325 = tg 25º → h 2 = 325. tg 25º pés = 151,6 pés
A altura total da torre é h 1 + h 2 = 263,2 + 151,6 pés = 414,7 pés.
Solução b
A janela está precisamente a uma altura h 2 do chão:
h 2 = 151,6 pés.
Referências
- Carena, M. 2019. Manual de Matemática Pré-Universidade. Universidade Nacional do Litoral.
- Hoffman, J. Seleção de tópicos de matemática. Volume 3.
- Jiménez, R. 2008. Álgebra. Prentice Hall.
- Stewart, J. 2006. Pré-cálculo: Matemática para Cálculo. 5 ª. Edição. Aprendizado Cengage.
- Zill, D. 1984. Álgebra e trigonometria. McGraw Hill.