Fatos sobre paralelogramos: definição, propriedades e usos

Início » Ciência » Matemática » Fatos sobre paralelogramos: definição, propriedades e usos

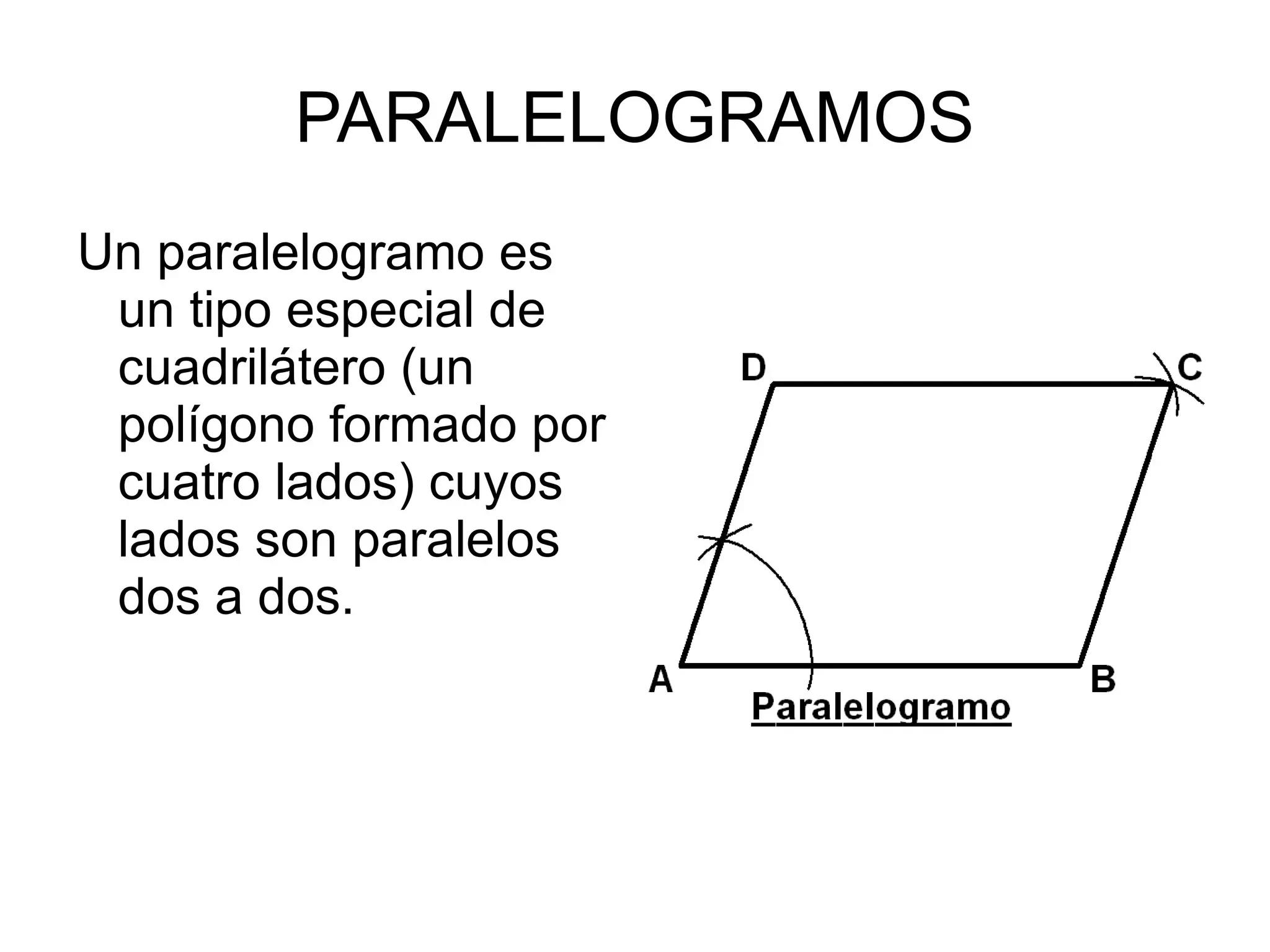
Os paralelogramos estão por toda parte: na engenharia, no design, na física dos vetores e em incontáveis problemas de geometria. Em essência, um paralelogramo é um quadrilátero cujos lados opostos são paralelos, o que desencadeia uma coleção elegante de propriedades sobre lados, ângulos, diagonais e áreas. A beleza do conceito é que ele aparece tanto na sala de aula quanto em aplicações reais.

Para além da definição, há uma trama de teoremas e recíprocas que vale a pena conhecer. Ângulos opostos iguais, lados opostos congruentes, diagonais que se bissetam e ângulos consecutivos suplementares são algumas peças desse quebra-cabeça matemático. E mais: se você pegar um retângulo e aplicar uma transformação de cisalhamento (um “empurrão” paralelo a um dos lados), o resultado é um paralelogramo — o que explica por que tantas fórmulas de área são estáveis sob deformações desse tipo.

O que é um paralelogramo e seus elementos

Um paralelogramo é um quadrilátero convexo e plano com dois pares de lados paralelos. Costumamos nomeá-lo como ABCD, em ordem, para falar de seus elementos e relações entre eles de forma clara.

Elementos estruturais indispensáveis aparecem sempre: quatro lados (AB, BC, CD, DA), quatro vértices (A, B, C, D), quatro ângulos internos (nos vértices A, B, C e D), quatro ângulos externos (suplementares aos internos) e duas diagonais (AC e BD). Esses componentes organizam-se de modo que os pares de lados opostos sejam paralelos, comportamento que rege todas as demais propriedades.

Desde cedo, aprende-se que em qualquer paralelogramo: lados opostos têm a mesma medida, ângulos opostos são congruentes, as diagonais se cruzam nos pontos médios e ângulos adjacentes (consecutivos) são suplementares. Essa estrutura implica que a soma dos ângulos internos (ou externos) é igual a 360°, o que é coerente com o fato de termos quatro cantos envolvendo um giro completo.

Propriedades fundamentais (e por que elas funcionam)

Uma propriedade-chave é: os lados opostos são congruentes. Traçando a diagonal AC em ABCD, os triângulos ADC e CBA são congruentes por um caso do tipo ângulo-lado-ângulo (ALA), pois os ângulos formados por pares de retas paralelas com a transversal AC são iguais (alternos internos) e AC é lado comum. Daí, conclui-se que AB = DC e AD = BC, além de relações de ângulos que aparecem a seguir.

Ainda com a mesma construção, nota-se que ângulos opostos são congruentes. Reescrevendo as medidas como somas de ângulos formados pela transversal com as retas paralelas, fica claro que os ângulos em B “espelham” os ângulos em D, e o mesmo ocorre para o par A e C. Esse encaixe mostra a razão geométrica da igualdade dos opostos.

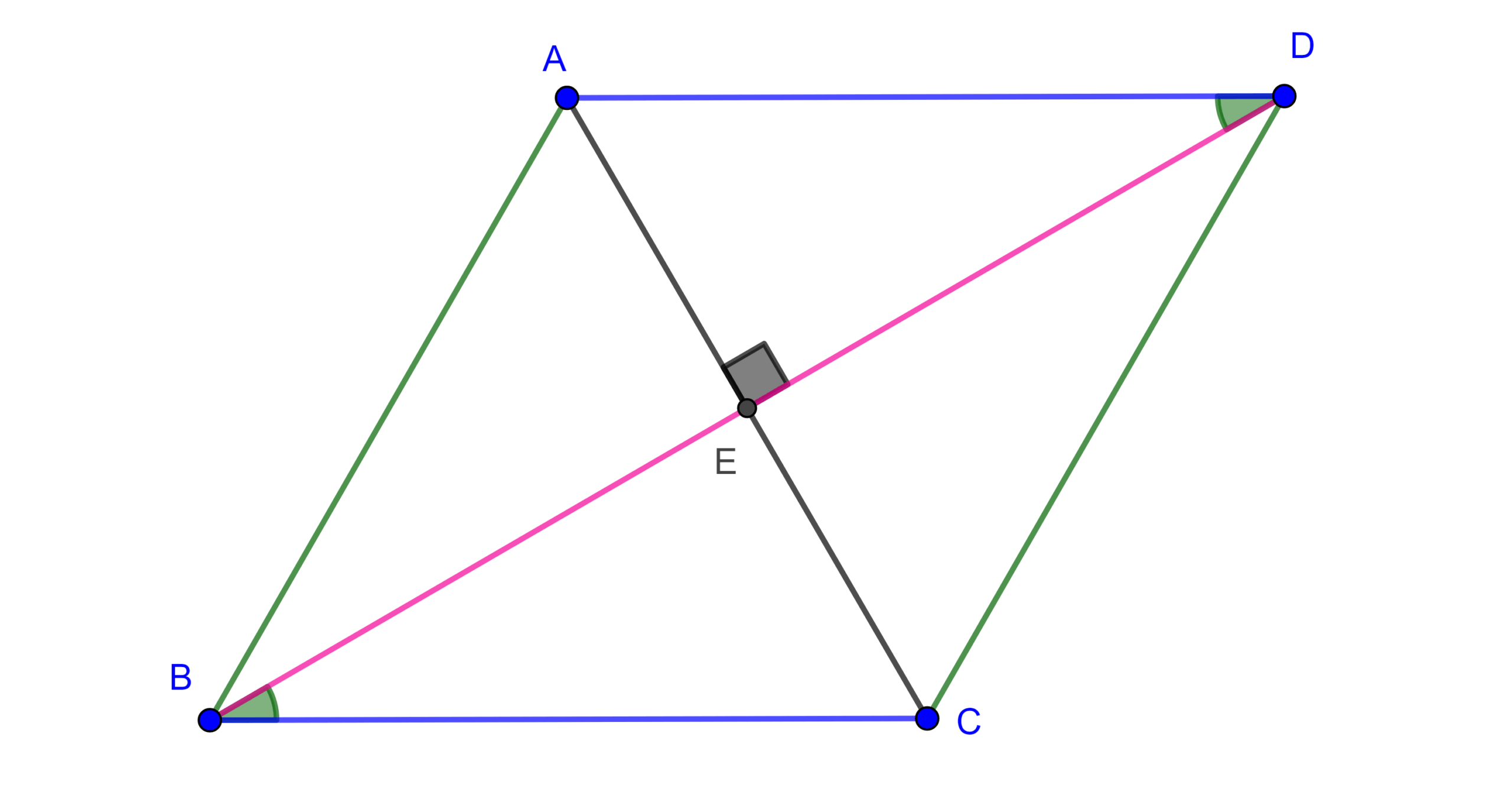
Outra joia dos paralelogramos: as diagonais se cortam nos respectivos pontos médios. Se E é a interseção de AC com BD, os triângulos CDE e ABE são congruentes por ALA, pois AB = CD (já visto), e ângulos correspondentes são iguais por paralelismo. Da congruência, obtemos AE = CE e BE = DE, ou seja, E bissecta as duas diagonais simultaneamente.

Consequência imediata do paralelismo: ângulos consecutivos são suplementares. Se AB é paralelo a CD e AD atua como transversal, o ângulo interno em D é correspondente ao ângulo externo adjacente em A, e este é suplementar do interno em A; portanto, os consecutivos somam 180°. Tudo se alinha: como há dois pares de ângulos suplementares, a soma dos internos (ou dos externos) totaliza 360°.

Recíprocas que caracterizam um paralelogramo

As propriedades anteriores também funcionam ao contrário, fornecendo critérios práticos de identificação. Se um quadrilátero convexo tem lados opostos congruentes, então é um paralelogramo. A ideia é que a congruência LLL (lado-lado-lado) entre os triângulos formados por uma diagonal força pares de ângulos internos alternos a coincidirem, implicando paralelismo entre lados opostos.

De modo análogo: se os ângulos opostos de um quadrilátero são congruentes, então os lados opostos são paralelos. Somando ângulos adjacentes e usando que o giro completo mede 360°, chega-se a pares de 180°, sinal de que retas correspondentes são paralelas. Com dois pares assim, estamos diante de um paralelogramo.

Outro teste clássico: se as diagonais de um quadrilátero se bissetam, o quadrilátero é um paralelogramo. A congruência LAL (lado-ângulo-lado) entre triângulos formados pelos semidiagonais assegura que lados opostos sejam congruentes; aplicada a ambos os pares, dispara o critério recíproco anterior e fecha a prova.

Ângulos, diagonais e triângulos internos

Do paralelismo resultam pares de ângulos alternos internos e correspondentes iguais, o que encadeia várias igualdades internas. Ângulos opostos iguais e consecutivos suplementares resumem bem a situação em qualquer vértice, assunto que volta quando falamos de retângulos, losangos e quadrados.

As diagonais AC e BD são centrais. Elas sempre se encontram no ponto médio uma da outra, e qualquer uma delas divide o paralelogramo em dois triângulos congruentes. Esse fato é muito útil tanto em problemas de demonstração quanto em aplicações de área e perímetro.

Uma observação física valiosa: para uma lâmina homogênea com forma de paralelogramo, o ponto de interseção das diagonais é um ponto de equilíbrio (centro de massa no plano). Não por acaso, esse mesmo ponto é a “chave” de muitas soluções em geometria vetorial.

Fórmulas essenciais: perímetro e área

Perímetro. Se a e b são os comprimentos de dois lados adjacentes, o perímetro é P = 2(a + b). Essa expressão resume o fato de que os lados opostos têm a mesma medida.

Área via base e altura. A fórmula mais lembrada é A = b · h, em que b é o comprimento de qualquer lado escolhido como base e h é a altura correspondente (distância perpendicular dessa base ao lado oposto). A invariância sob cisalhamento explica por que a área não muda quando “entortamos” um retângulo, desde que preservemos base e altura.

Área via dois lados e ângulo. Se conhecemos os comprimentos de dois lados adjacentes a e b e o ângulo α entre eles, A = a · b · sen(α). Essa sentença é um “primo” da conhecida fórmula para áreas de triângulos usando o seno do ângulo entre dois lados.

Área via diagonais. Se d1 e d2 são as diagonais e α é um dos ângulos formados entre elas, vale A = (d1 · d2 · sen(α))/2. A justificativa agrega quatro triângulos formados pelas diagonais, em pares congruentes, e usa a identidade trigonométrica sen(α) = sen(180° − α).

Relação com triângulos. Pela decomposição “corta-e-encaixa”, um paralelogramo pode ser transformado em um triângulo de mesma base e altura, deixando claro por que A = b · h funciona; esse princípio também aparece em deduções de fórmulas para polígonos e, mais tarde, para áreas com integrais.

Tipos especiais: retângulo, losango e quadrado

Retângulo. É um paralelogramo de ângulos internos retos (90°). Todos os retângulos têm diagonais congruentes, além de herdar todas as propriedades gerais: lados opostos paralelos/congruentes, diagonais que se bissetam e ângulos consecutivos suplementares.

Losango. É o paralelogramo em que todos os lados são congruentes. Sua marca registrada: as diagonais são perpendiculares. Embora as diagonais não precisem ser iguais, elas se cruzam em 90° e continuam se bissetando mutuamente.

Quadrado. Combina os dois mundos: lados congruentes e ângulos de 90°. No quadrado, as diagonais são ao mesmo tempo congruentes e perpendiculares. Por isso, todo quadrado é simultaneamente um retângulo e um losango.

Relações e classificações. É correto afirmar que: todo retângulo é paralelogramo, todo losango é paralelogramo, todo quadrado é retângulo e losango e, portanto, paralelogramo. Por outro lado, não é verdade que: todo paralelogramo seja retângulo, losango ou quadrado, nem que todo retângulo ou losango seja quadrado.

Critérios práticos e testes rápidos

Na prática, vários atalhos ajudam a reconhecer um paralelogramo: dois pares de lados opostos paralelos (definição), dois pares de lados opostos congruentes (recíproca), ângulos opostos congruentes (recíproca) ou diagonais que se bissetam (recíproca). Qualquer um desses “gatilhos” num quadrilátero convexo basta para cravar o veredito.

No plano cartesiano, existem checagens algébricas úteis. Vetores colineares e iguais em módulo apontando em sentidos opostos para lados opostos confirmam paralelismo e congruência. Outra via é verificar se os pontos médios das diagonais coincidem — uma condição fácil de computar e extremamente robusta.

Aplicações: vetores, engenharia, design e computação

Em física e engenharia, a regra do paralelogramo para soma de vetores e o produto cruzado são onipresentes: dados dois vetores como lados adjacentes de um paralelogramo, a diagonal representa o vetor resultante. Esse diagrama gráfico é ferramenta de primeira ordem para equilíbrio de forças.

Na arquitetura e no design, padrões geométricos com simetrias baseadas em paralelogramos trazem regularidade, repetição e eficiência de material. Em computação gráfica e visão computacional, transformações afins (como cisalhamento) fazem surgir paralelogramos a partir de retângulos, preservando áreas e alinhamentos projetados quando necessário.

Na geometria analítica e álgebra linear, subespaços, bases e operadores lineares podem ser visualizados via paralelogramos formados por vetores, ajudando tanto em intuição quanto em provas. O tema ainda toca tópicos de geometria euclidiana clássica e motiva exercícios em otimização e modelagem.

Propriedades avançadas: trissectrizes e o “paralelogramo de Morley”

Há um resultado curioso que ecoa o famoso teorema de Morley (para triângulos): considere as trissectrizes de ângulos adjacentes de um paralelogramo e tome os pontos de interseção correspondentes dois a dois, avançando ao longo do contorno. Quando esses pontos não são colineares, obtém-se um novo paralelogramo.

Mais surpresas: se o paralelogramo original for um retângulo, a figura obtida é um losango; em contrapartida, se o original for um losango, o resultado é um retângulo. Outras escolhas de pares de trissectrizes (não as adjacentes “padrão”) também levam ou a colinearidade ou a outro paralelogramo, mantendo essa dualidade retângulo-losango nas situações especiais.

Vocabulário essencial

Paralelogramo: quadrilátero plano com lados opostos paralelos e de mesmo comprimento.

Congruente: objetos geométricos com mesma forma e tamanho (coincidem por isometrias).

Ângulo: abertura entre duas semirretas com origem comum; interno no vértice do polígono ou externo, suplementar ao interno correspondente.

Base e altura: a base é o lado escolhido para medir área; a altura é a distância perpendicular dessa base ao lado oposto.

Perímetro e área: soma dos lados e medida da superfície; para paralelogramos, P = 2(a + b) e A = b · h (ou fórmulas equivalentes com seno e diagonais).

Diagonal: segmento que conecta vértices não consecutivos; em paralelogramos, elas se bissetam no ponto de encontro.

Vetores: entidades com direção, sentido e magnitude; o paralelogramo modela sua soma gráfica.

Geometria euclidiana e analítica: estudos das figuras no plano clássico e via coordenadas/equações, respectivamente; ambas sustentam as propriedades listadas.

Fatos rápidos e úteis

Alguns lembretes de bolso: as diagonais de todo paralelogramo se bissetam; os ângulos opostos são iguais; os consecutivos somam 180°; a soma dos internos (e dos externos) é 360°; e as áreas são calculáveis por base-altura, lados-seno ou diagonais-seno. Para completar, o ponto médio comum das diagonais é um “centro de equilíbrio” de uma lâmina uniforme com essa forma.

Exercícios resolvidos

1) Área de um paralelogramo com base 10 cm e altura 5 cm. Pela fórmula, A = b · h = 10 · 5 = 50 cm². Sem mistério: a altura é perpendicular à base, e a decomposição em retângulos/triângulos confirma o resultado.

2) Perímetro de um paralelogramo com lados 4 cm e 5 cm. Como lados opostos são congruentes, P = 2(a + b) = 2(4 + 5) = 18 cm. Essa expressão independe do ângulo interno; só importa o par de comprimentos adjacentes.

Notas históricas e conexões

Da geometria clássica aos nossos dias, Euclides consolidou propriedades sobre paralelismo e ângulos, enquanto Descartes levou a discussão ao plano cartesiano, facilitando demonstrações algébricas. Em épocas mais recentes, desenvolvimentos em topologia e geometrias não euclidianas ampliaram a compreensão das figuras, embora o paralelogramo permaneça firmemente ancorado na geometria plana euclidiana.

Para a educação e a prática, vale usar recursos dinâmicos (softwares de geometria) para manipular vértices A, B, C, D e visualizar como ângulos, lados e diagonais reagem. A exploração ativa fortalece a intuição e encurta o caminho para as provas e aplicações.

Ao percorrer definição, propriedades, recíprocas, fórmulas, casos especiais e até resultados avançados com trissectrizes, fica claro por que os paralelogramos são tão presentes. Da sala de aula às engenharias, compreender essa figura é dominar um alicerce da geometria plana, com reflexos diretos no tratamento de ângulos, áreas, vetores e transformações.