Os graus de liberdade são um conceito estatístico fundamental que desempenha um papel crucial na determinação da precisão das estimativas e dos testes de hipóteses. Eles representam o número de valores independentes que podem variar em um conjunto de dados ou em um modelo estatístico.
Neste contexto, os graus de liberdade podem ser calculados de diferentes maneiras, dependendo do tipo de teste estatístico ou modelo em questão. Por exemplo, no caso de uma distribuição t de Student, os graus de liberdade são determinados pelo tamanho da amostra menos um.
Existem diferentes tipos de graus de liberdade, como os graus de liberdade associados a uma estimativa pontual, aos resíduos de um modelo de regressão ou aos parâmetros de um modelo de ANOVA.
Alguns exemplos práticos de aplicação dos graus de liberdade incluem a realização de testes de hipóteses, a determinação de intervalos de confiança e a avaliação da significância estatística de um modelo.
Descubra a fórmula para determinar a quantidade de graus de liberdade em um experimento.
Graus de liberdade: como calculá-los, tipos, exemplos.
Os graus de liberdade são um conceito fundamental em estatística, que nos permite entender a variabilidade dos dados em um experimento. Eles representam o número de observações independentes que contribuem para a estimativa de um parâmetro estatístico.
Para determinar a quantidade de graus de liberdade em um experimento, podemos usar a seguinte fórmula:
Graus de liberdade = número total de observações – número de restrições
Por exemplo, se estamos realizando um experimento com 50 observações e impomos uma restrição que reduz a liberdade dos dados em 10 observações, então teremos:
Graus de liberdade = 50 – 10 = 40
Existem diferentes tipos de graus de liberdade, como os graus de liberdade do modelo e os graus de liberdade do erro. Os graus de liberdade do modelo representam o número de parâmetros estimados no modelo, enquanto os graus de liberdade do erro representam a variabilidade não explicada pelo modelo.
Ao calcular corretamente os graus de liberdade, podemos fazer inferências precisas e tomar decisões fundamentadas com base nos resultados obtidos.
Descubra facilmente seu nível de liberdade através de algumas etapas simples.
Entender os graus de liberdade pode ser uma tarefa complicada para muitas pessoas, mas na verdade, é mais simples do que parece. Para calcular seus graus de liberdade, você pode seguir algumas etapas simples que irão te ajudar a ter uma ideia mais clara do seu nível de liberdade.
Primeiramente, é importante saber que os graus de liberdade representam o número de valores independentes que podem variar em um cálculo estatístico. Eles são essenciais para determinar a precisão de uma estimativa ou de um teste estatístico. Para calculá-los, você precisa conhecer o número de observações e o número de parâmetros estimados no modelo.
Existem diferentes tipos de graus de liberdade, como os graus de liberdade do erro e os graus de liberdade do modelo. Os graus de liberdade do erro representam a quantidade de liberdade que resta depois de considerar todas as restrições impostas pelo modelo, enquanto os graus de liberdade do modelo representam o número de parâmetros estimados no modelo.
Um exemplo simples seria o seguinte: se você tem 10 observações e está ajustando um modelo linear simples com uma única variável independente, então o número de graus de liberdade do modelo seria 1, e o número de graus de liberdade do erro seria 9.
Seguindo essas etapas simples, você poderá descobrir facilmente o seu nível de liberdade e utilizá-lo da melhor forma possível em suas análises estatísticas.
Como determinar o número de graus de liberdade em uma análise de variância?
Para determinar o número de graus de liberdade em uma análise de variância, é necessário considerar a quantidade de informação disponível e o número de restrições impostas ao modelo estatístico. Os graus de liberdade representam a quantidade de variabilidade que pode ser atribuída a cada fonte de variação em um estudo. Eles são essenciais para calcular a significância estatística dos resultados obtidos.
Em uma análise de variância, os graus de liberdade são calculados subtraindo o número de restrições impostas ao modelo estatístico do número total de observações. Por exemplo, em um estudo com 100 observações e três grupos, o número de graus de liberdade para os grupos seria 3-1=2. Isso significa que há dois graus de liberdade para testar as diferenças entre os grupos.
Existem diferentes tipos de graus de liberdade, como os graus de liberdade do modelo, os graus de liberdade do erro e os graus de liberdade totais. Cada um deles desempenha um papel específico na análise estatística e na interpretação dos resultados.
Eles são calculados com base no número de restrições impostas ao modelo estatístico e no número total de observações disponíveis.
Quantos graus de liberdade há?
Os graus de liberdade referem-se ao número de elementos independentes em um sistema que podem variar de forma independente. Em outras palavras, são as diferentes maneiras pelas quais um sistema pode se mover ou mudar. Para calcular os graus de liberdade de um sistema, basta subtrair o número de restrições impostas ao sistema do número total de variáveis.
Existem diferentes tipos de graus de liberdade, dependendo do sistema em questão. Por exemplo, em um sistema de partículas, os graus de liberdade são as coordenadas espaciais e as velocidades das partículas. Já em um sistema mecânico, os graus de liberdade podem ser os ângulos de rotação e as distâncias entre as peças.
Um exemplo simples de cálculo de graus de liberdade pode ser visto em um pêndulo simples. Neste caso, o pêndulo tem um bgrau de liberdadeb, que pode ser representado pelo ângulo de oscilação da massa. Se adicionarmos um amortecedor ao sistema, reduzimos o número de graus de liberdade para zero, pois o movimento do pêndulo fica restrito.
Eles são calculados subtraindo o número de restrições do número total de variáveis do sistema. Entender os graus de liberdade de um sistema é fundamental para analisar seu comportamento e prever sua evolução ao longo do tempo.
Graus de liberdade: como calculá-los, tipos, exemplos

Os graus de liberdade nas estatísticas são o número de componentes independentes de um vetor aleatório. Se o vetor tem n componentes e existem p equações lineares que relacionam seus componentes, o grau de liberdade é np.
O conceito de graus de liberdade também aparece na mecânica teórica, onde aproximadamente são equivalentes à dimensão do espaço onde a partícula se move, menos o número de ligaduras.
Este artigo discutirá o conceito de graus de liberdade aplicado à estatística, mas um exemplo mecânico é mais fácil de visualizar geometricamente.
Tipos de graus de liberdade
Dependendo do contexto em que é aplicada, a maneira de calcular o número de graus de liberdade pode variar, mas a ideia subjacente é sempre a mesma: dimensões gerais menos número de restrições.
Em um caso mecânico
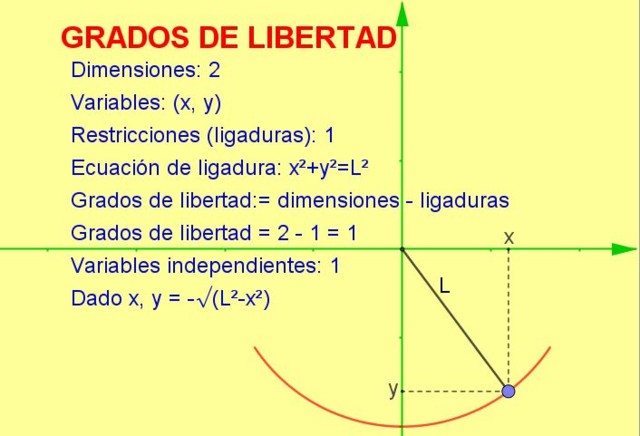
Considere uma partícula oscilante amarrada a uma corda (um pêndulo) que se move no plano vertical xy (2 dimensões). No entanto, a partícula é forçada a se mover pela circunferência do raio igual ao comprimento da corda.
Como a partícula só pode se mover nessa curva, o número de graus de liberdade é 1. Isso pode ser visto na figura 1.
A maneira de calcular o número de graus de liberdade é tomando a diferença no número de dimensões menos o número de restrições:
graus de liberdade: = 2 (dimensões) – 1 (ligadura) = 1
Outra explicação que nos permite chegar ao resultado é a seguinte:
-Sabemos que a posição em duas dimensões é representada por um ponto de coordenada (x, y).
-Mas como o ponto deve satisfazer a equação do círculo (x 2 + y 2 = L 2 ) para um determinado valor da variável x, a variável y é determinada pela referida equação ou restrição.
Assim, apenas uma das variáveis é independente e o sistema possui um (1) grau de liberdade .
Em um conjunto de valores aleatórios
Para ilustrar o significado do conceito, suponha que o vetor
x = (x 1 , x 2 ,…, x n )
Representando a amostra de n valores aleatórios normalmente distribuídos. Nesse caso, o vetor aleatório x tem n componentes independentes e, portanto, diz-se que x tem n graus de liberdade .
Agora vamos construir o vetor r dos resíduos
r = (x 1 – <x>, x 2 – <x>,…., x n – <x>)
Onde <x> representa a média da amostra, que é calculada assim:
<x> = (x 1 + x 2 +…. + x n ) / n
Então a soma
(x 1 – <x>) + (x 2 – <x>) +…. + (x n – <x>) = (x 1 + x 2 +…. + x n ) – n <x> = 0
É uma equação que representa uma restrição (ou ligação) nos elementos do vetor r dos resíduos, uma vez que se são conhecidos componentes n-1 do vetor r , a equação da restrição determina o componente desconhecido.
Portanto, o vetor r da dimensão n com a restrição:
X (x i – <x>) = 0
Possui (n – 1) graus de liberdade .
Novamente, aplica-se que o cálculo do número de graus de liberdade é:
graus de liberdade: = n (dimensões) – 1 (restrições) = n-1
Exemplos
Variação e graus de liberdade
A variância s 2 é definida como a média do quadrado dos desvios (ou resíduos) da amostra de n dados:
s 2 = ( r • r ) / (n-1)
onde r é o vetor dos resíduos r = (x1 – <x>, x2 – <x>,…., xn – <x>) e o ponto espesso ( • ) é o operador do produto escalar . Como alternativa, a fórmula de variação pode ser escrita da seguinte maneira:
s 2 = ∑ (x i – <x>) 2 / (n-1)
De qualquer forma, deve-se notar que, ao calcular a média do quadrado dos resíduos, ele é dividido entre (n-1) e não entre n, pois, como discutido na seção anterior, o número de graus de liberdade do vetor r é ( n-1).
Se para o cálculo da variância fosse dividido por n em vez de (n-1), o resultado teria um viés muito significativo para valores de n inferiores a 50.
A fórmula de variância também aparece na literatura com o divisor n em vez de (n-1), quando se trata da variância de uma população.
Mas o conjunto da variável aleatória dos resíduos, representado pelo vetor r , embora tenha a dimensão n, possui apenas (n-1) graus de liberdade. No entanto, se o número de dados for grande o suficiente (n> 500), ambas as fórmulas convergem para o mesmo resultado.
Calculadoras e planilhas oferecem as duas versões da variação e o desvio padrão (que é a raiz quadrada da variação).
Nossa recomendação, tendo em vista a análise aqui apresentada, é sempre escolher a versão com (n-1) sempre que for necessário calcular a variância ou desvio padrão, para evitar resultados tendenciosos.
Na distribuição do quadrado do Chi
Algumas distribuições de probabilidade em variável aleatória contínua dependem de um parâmetro chamado grau de liberdade , é o caso da distribuição do quadrado do Chi (χ 2 ).
O nome desse parâmetro vem precisamente dos graus de liberdade do vetor aleatório subjacente ao qual essa distribuição é aplicada.
Suponha que você tenha g populações, das quais são retiradas amostras de tamanho n:
X 1 = (x1 1 , x1 2 ,… ..x1 n )
X 2 = (x2 1 , x2 2 ,… ..x2 n )
…
X j = (xj 1 , xj 2 ,… ..xj n )
…
Xg = (xg 1 , xg 2 ,… xx n )
Uma população j com média <Xj> e desvio padrão Sj segue a distribuição normal N ( <Xj>, Sj ).
A variável tipificada ou normalizada zj i é definida como:
zj i = (xj i – <Xj> ) / Sj .
E o vetor Zj é definido assim:
Zj = ( zj 1 , zj 2 ,…, zj i ,…, zj n ) e segue a distribuição normal normalizada N (0,1).
Então a variável:
Q = ((z1 1 ^ 2 + z2 1 ^ 2 +…. + Zg 1 ^ 2),…., (Z1 n ^ 2 + z2 n ^ 2 +…. + Zg n ^ 2))
segue a distribuição χ 2 (g) chamada distribuição qui-quadrado com grau de liberdade g.
No teste de hipótese (com exemplo resolvido)
Quando você deseja fazer um teste de hipótese com base em um determinado conjunto de dados aleatórios, precisa saber o número de graus de liberdade g para poder aplicar o teste do quadrado do Chi.
Como exemplo, analisaremos os dados coletados sobre as preferências de sorvetes de chocolate ou morango entre homens e mulheres em uma determinada sorveteria. A frequência com que homens e mulheres escolhem morango ou chocolate está resumida na figura 2.
Primeiro, é calculada a tabela de frequência esperada, que é preparada multiplicando o número total de linhas pelo número total de colunas, dividido pelo total de dados . O resultado é mostrado na figura a seguir:
Em seguida, procedemos ao cálculo do quadrado do Chi (a partir dos dados) usando a seguinte fórmula:
χ 2 = ∑ (F o – F e ) 2 / F e
Onde F o são as frequências observadas (Figura 2) e F e são as frequências esperadas (Figura 3). A soma abrange todas as linhas e colunas, que em nosso exemplo fornecem quatro termos.
Depois de fazer as operações, você obtém:
χ 2 = 0,2043.
Agora é necessário comparar com o quadrado qui teórico, que depende do número de graus de liberdade g .
No nosso caso, esse número é determinado da seguinte maneira:
g = (#rows – 1) (#columns – 1) = (2-1) (2-1) = 1 * 1 = 1.
Acontece que o número de graus de liberdade g neste exemplo é 1.
Se você deseja testar ou rejeitar a hipótese nula (H0: não há correlação entre SABOR e GÊNERO) com um nível de significância de 1%, é calculado o valor teórico do quadrado do qui com grau de liberdade g = 1.
O valor que faz a frequência acumulada é (1 – 0,01) = 0,99, ou seja, 99%, é pesquisado. Este valor (que pode ser obtido das tabelas) é 6.636.
Como o Chi teórico excede o Chi calculado, a hipótese nula é verificada.
Em outras palavras, com os dados coletados, não se observa relação entre as variáveis SABOR e GÊNERO.
Referências
- Minitab. O que são graus de liberdade? Recuperado de: support.minitab.com.
- Moore, David. (2009) Estatísticas básicas aplicadas. Editor de Antoni Bosch.
- Leigh, Jennifer. Como calcular graus de liberdade em modelos estatísticos. Recuperado de: geniolandia.com
- Wikipedia. Grau de liberdade (estatística). Recuperado de: es.wikipedia.com
- Wikipedia. Grau de liberdade (físico). Recuperado de: es.wikipedia.com