O triângulo agudo é um tipo de triângulo no qual todos os seus ângulos internos são menores que 90 graus. Essa característica faz com que as medidas dos lados sejam proporcionais aos ângulos, resultando em formas mais alongadas e agudas. Existem diferentes tipos de triângulos agudos, como o triângulo equilátero, isósceles e escaleno, cada um com propriedades e características específicas. Neste artigo, exploraremos mais sobre as características e os tipos de triângulos agudos.
Descubra os três tipos de triângulo em apenas uma leitura rápida!
Os triângulos são figuras geométricas formadas por três lados e três ângulos. Existem três tipos principais de triângulos: equilátero, isósceles e escaleno.
O triângulo equilátero possui os três lados iguais e os três ângulos internos iguais a 60 graus. Já o triângulo isósceles possui dois lados iguais e dois ângulos iguais. Por fim, o triângulo escaleno possui os três lados e os três ângulos diferentes entre si.
É importante conhecer essas características para identificar corretamente cada tipo de triângulo em problemas de geometria ou em situações do dia a dia. Agora que você sabe mais sobre os três tipos de triângulo, fica mais fácil reconhecê-los e utilizá-los em seus estudos ou em situações práticas.
Significado do triângulo agudo: conceito, características e propriedades do ângulo menor que 90°.
O triângulo agudo é um tipo de triângulo que possui um ângulo menor que 90°. Isso significa que em um triângulo agudo, todos os seus ângulos internos são agudos, ou seja, menores que 90°. Essa característica faz com que o triângulo agudo tenha propriedades únicas que o distinguem dos outros tipos de triângulos.
Uma das principais propriedades do triângulo agudo é que a soma de seus três ângulos internos sempre será igual a 180°. Isso ocorre porque a soma de todos os ângulos de um triângulo é sempre igual a 180°, independentemente do tipo de triângulo.
Além disso, o triângulo agudo pode ser classificado de acordo com os tamanhos de seus ângulos. Por exemplo, um triângulo agudo pode ser equilátero, quando possui os três ângulos iguais a 60°, ou escaleno, quando possui os três ângulos diferentes entre si.
Em resumo, o triângulo agudo é um tipo de triângulo que possui ângulos menores que 90° e apresenta propriedades específicas, como a soma de seus ângulos internos igual a 180° e a possibilidade de ser classificado de acordo com os tamanhos de seus ângulos.
Qual é a medida dos lados de um triângulo agudo?
Um triângulo agudo é um triângulo no qual todos os ângulos internos são agudos, ou seja, têm medida inferior a 90 graus. Nesse tipo de triângulo, os lados também possuem medidas específicas. A medida dos lados de um triângulo agudo pode variar, mas sempre será menor do que a medida dos lados de um triângulo obtuso ou um triângulo reto.
Para determinar a medida dos lados de um triângulo agudo, é importante lembrar que a soma das medidas de dois lados quaisquer sempre será maior do que a medida do terceiro lado. Além disso, a medida do lado oposto ao ângulo agudo será sempre maior do que a medida dos outros dois lados.
Portanto, em um triângulo agudo, os lados podem ter diversas medidas, mas sempre respeitando a relação de desigualdade entre eles. É importante ter em mente que a classificação de um triângulo como agudo não está relacionada apenas com a medida de seus lados, mas também com a medida de seus ângulos internos.
Quantos graus mede a soma dos ângulos internos de um triângulo agudo?
Um triângulo agudo é um triângulo que possui todos os seus ângulos internos menores que 90 graus. Essa característica faz com que a soma dos ângulos internos de um triângulo agudo seja sempre igual a 180 graus. Isso significa que, mesmo sendo um triângulo com ângulos mais fechados, a soma total dos seus ângulos internos ainda será a mesma que a de qualquer outro triângulo, independente do tipo.
Triângulo agudo: características e tipos
Os triângulos agudas são aqueles cujos três ângulos internos são ângulos agudos; isto é, a medida de cada um desses ângulos é inferior a 90 graus. Não tendo ângulo reto, temos que o teorema de Pitágoras não é cumprido para esta figura geométrica.
Portanto, se queremos ter algum tipo de informação sobre qualquer um de seus lados ou ângulos, é necessário fazer uso de outros teoremas que nos permitem ter acesso aos referidos dados. O que podemos usar são o teorema do seno e o teorema do cosseno.
Caracteristicas
Entre as características dessa figura geométrica, podemos destacar aquelas que são dadas pelo simples fato de ser um triângulo. Entre estes, temos que:
– Um triângulo é um polígono que tem três lados e três ângulos.
– A soma de seus três ângulos internos é igual a 180 °.
– A soma de dois dos seus lados é sempre maior que o terceiro.
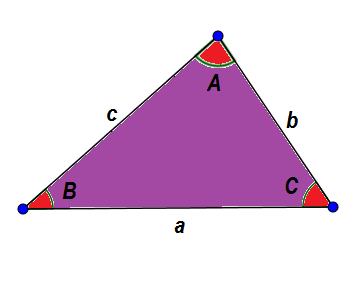
Como exemplo, vejamos o seguinte triângulo ABC. Em geral, identificamos os lados com uma letra minúscula e seus ângulos com uma letra maiúscula, de modo que um lado e seu ângulo oposto tenham a mesma letra.
Devido às características já apresentadas, sabemos que:
A + B + C = 180 °
a + b> c, a + c> b e b + c> a
A principal característica que distingue esse tipo de triângulo do resto é que, como já mencionamos, seus ângulos internos são agudos; isto é, a medida de cada um dos seus ângulos é menor que 90 °.
Acutengles, juntamente com triângulos obtusos (aqueles em que um de seus ângulos tem uma medida maior que 90 °), fazem parte do conjunto de triângulos oblíquos. Este conjunto é formado por triângulos que não são retângulos.
Como parte dos triângulos oblíquos, temos que ser capazes de resolver problemas onde os triângulos intervenientes intervêm, devemos fazer uso do teorema do seno e do teorema do cosseno.
Teorema do Seno
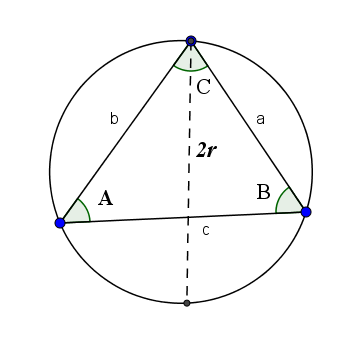
O teorema do seno nos diz que a razão de um lado com o seno de seu ângulo oposto é duas vezes o raio do círculo formado pelos três vértices desse triângulo. Quer dizer:
2r = a / sen (A) = b / sen (B) = c / sen (C)
Teorema do cosseno
Por outro lado, o teorema do cosseno nos fornece essas três igualdades para qualquer triângulo ABC:
a 2 = b 2 + c 2 -2bc * cos (A)
b 2 = a 2 + c 2 -2ac * cos (B)
c 2 = a 2 + b 2 -2ab * cos (C)
Esses teoremas também são conhecidos como lei seno e lei cosseno, respectivamente.
Outra característica que podemos dar dos triângulos agudos é que dois deles são iguais se atenderem a algum dos seguintes critérios:
– Se eles têm três lados iguais.
– Se eles têm um lado e dois ângulos iguais um ao outro.
– Se eles têm dois lados iguais e um ângulo.
Tipos
Os ângulos agudos podem ser classificados de acordo com os lados. Estes podem ser:
Triângulos aquáticos equilaterais
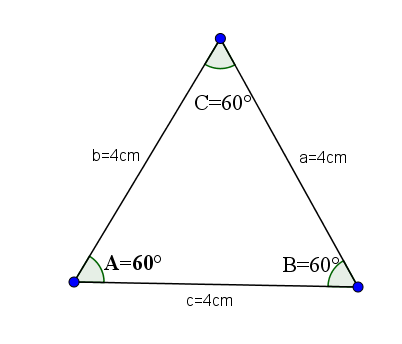
São os triângulos agudos que têm todos os seus lados iguais e, portanto, todos os seus ângulos internos têm o mesmo valor, que é A = B = C = 60 ° graus.
Como exemplo, vamos pegar o triângulo a seguir, cujos lados a, bec têm valor 4.
Triângulos aquáticos isósceles
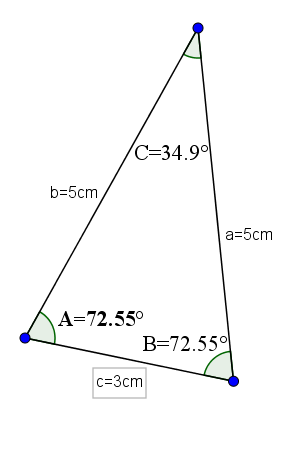
Esses triângulos, além de terem ângulos internos agudos, têm a característica de ter dois lados iguais e o terceiro, que geralmente é tomado como base, diferente.
Um exemplo desse tipo de triângulos pode ser aquele cuja base é 3 e seus outros dois lados têm um valor de 5. Com essas medidas, você teria ângulos opostos aos lados iguais com o valor de 72,55 ° e o ângulo oposto de a base seria 34,9 °.
Ângulos agudos escaleno
Estes são os triângulos que têm todos os lados diferentes, dois a dois. Portanto, todos os seus ângulos, além de serem inferiores a 90 °, são diferentes de dois a dois.
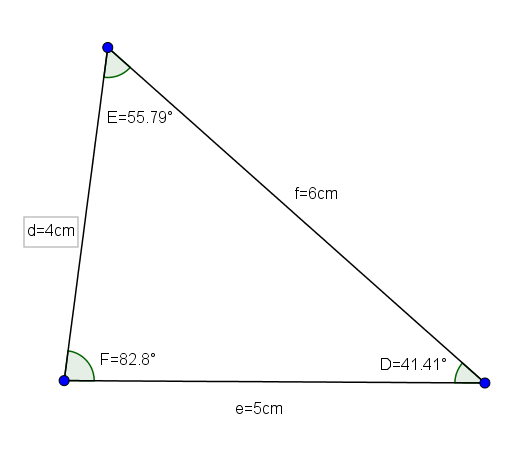
O triângulo DEF (cujas medidas são d = 4, e = 5 ef = 6 e seus ângulos são D = 41,41 °, E = 55,79 ° e F = 82,8 °) é um bom exemplo de um triângulo agudo Scalene
Resolução de triângulos agudos
Como dissemos anteriormente, para a resolução de problemas em que triângulos agudos intervêm, é necessário o uso dos teoremas seno e cosseno.
Exemplo 1
Dado um triângulo ABC com ângulos A = 30 °, B = 70 ° e lateralmente a = 5cm, queremos saber o valor do ângulo C e os lados bec.
A primeira coisa que fazemos é usar o fato de que a soma dos ângulos internos de um triângulo é de 180 °, a fim de obter o valor do ângulo C.
180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C
Limpamos C e temos:
C = 180 ° – 100 ° = 80 °
Como já sabemos os três ângulos e um lado, podemos usar o teorema do seno para determinar o valor dos lados restantes. Para o teorema, precisamos:
a / sen (A) = b / sen (B) e a / sen (A) = c / (sen (C)
Limpamos b da equação e temos que:
b = (a * sen (B)) / sen (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4
Agora só precisamos calcular o valor de c. Prosseguimos da mesma maneira que no caso anterior:
c = (a * sen (C)) / sen (A) ≈ (5 * 0,984) / (0,5) ≈ 9,84
Assim, obtemos todos os dados do triângulo. Como podemos ver, esse triângulo se enquadra na categoria de triângulo agudo escaleno.
Exemplo 2
Dado um triângulo DEF com lados d = 4cm, e = 5cm ef = 6cm, queremos saber o valor dos ângulos desse triângulo.
Para este caso, usaremos a lei do cosseno, que nos diz que:
d 2 = e 2 + f 2 – 2ecos (D)
A partir desta equação, podemos limpar cos (D), o que resulta em:
Cos (D) = ((4) 2 – (5) 2 – (6) 2 ) / (- 2 * 5 * 6) = 0,75
A partir daqui, temos que D≈ 41,41 °
Usando agora o teorema do senom, temos a seguinte equação:
d / (sen (D) = e / (sen (E)
Compensando sen (E), temos que:
sen (E) = e * sen (D) / d = (5 * 0,66) / 4 ≈ 0,827
A partir daqui, temos a E≈55,79 °
Finalmente, usando que a soma dos ângulos internos de um triângulo seja 180 °, temos que F≈82,8 °.
- Landaverde, F. d. (1997). Geometria (Reimpressão ed.). Progresso
- Leake, D. (2006). Triângulos (ilustração ilustrada). Heinemann-Raintree.
- Leal G. Juan Manuel (2003). Geometria métrica plana.
- Ruiz, Á .; Barrantes, H. (2006). Geometrias Tecnologia CR.
- Sullivan, M. (1997). Trigonometria e Geometria Analítica. Pearson Education.