- Conceitos e classificações: diferenças entre frações próprias, impróprias, aparentes, irredutíveis e mistas.
- Conversões equivalentes: impróprias em mistas (parte inteira + fração própria) e mistas em impróprias.
- Operações e simplificação: uso de MMC, soma/subtração, multiplicação/divisão e irredutibilidade.
Frações impróprias e próprias aparecem em todo lugar, do caderno de Matemática à cozinha de casa, e entender como ir de uma para outra é um atalho poderoso para ganhar fluência numérica. Aqui você vai ver, de forma direta e cheia de exemplos, como converter uma fração imprópria em uma fração própria via número misto (separando parte inteira e parte fracionária), por que isso funciona e quando usar — e pode consultar exemplos e exercícios sobre tipos de fração para praticar.
Além do passo a passo, vamos revisar os tipos de fração, simplificação (irredutibilidade), operações, aplicações, exercícios resolvidos e um glossário com os termos essenciais. Para quem curte aprender com vídeo, vale lembrar que videoaulas sobre “tipos de fração” são um ótimo complemento, mas aqui você encontrará uma explicação completa e prática, no melhor estilo “mão na massa”.
O que é uma fração e como ler seus termos
Quando representamos uma quantidade como a/b, o número de cima é o numerador (quantas partes temos) e o de baixo é o denominador (em quantas partes iguais o todo foi dividido). Assim, 3/4 indica 3 partes de um total que foi dividido em 4 pedaços do mesmo tamanho. Para detalhes sobre cada componente, veja as partes da fração.
Do ponto de vista de valor, frações menores que 1 (numerador menor que denominador) são chamadas de próprias, enquanto frações com numerador maior ou igual ao denominador têm valor igual ou acima de 1 e recebem o nome de impróprias. Esse contraste ajuda a prever o comportamento da fração em cálculos e comparações; está ligado ao estudo de números racionais.
Tipos de fração
Fração própria
Chamamos de própria a fração em que numerador < denominador, ou seja, o valor numérico é menor que 1. Exemplos típicos são 1/2, 5/9 e 6/13, todos com a parte superior menor que a inferior, o que garante um resultado abaixo da unidade.
Fração imprópria
Já as impróprias são aquelas em que numerador >= denominador, gerando um valor maior ou igual a 1. Exemplos comuns: 13/5, 8/7 e 15/11. Nesses casos, há “uma ou mais unidades completas” contidas na fração.
Uma observação útil: muitas vezes é vantajoso reescrever a fração imprópria como número misto (parte inteira + fração), pois isso facilita a interpretação em contexto prático.
Fração aparente
Uma fração é aparente quando o resultado da divisão entre numerador e denominador é um número inteiro exato. Por exemplo, 12/4 = 3 e 35/7 = 5. Nesse caso, a fração “desaparece” e vira um inteiro puro.
Fração irredutível
Uma fração está na forma irredutível quando numerador e denominador não compartilham divisores comuns além de 1. É o ponto em que a fração não pode mais ser simplificada. Exemplos: 3/5, 2/9 e 13/18.
Como simplificar frações (até chegar à forma irredutível)
Para simplificar, divida numerador e denominador por um divisor comum até que não reste nenhum além de 1. Por exemplo, em 12/15, ambos os termos são divisíveis por 3, resultando em 4/5. Esta é a forma irredutível, pois 4 e 5 são coprimos.
Fração mista
O número misto é uma maneira alternativa de escrever uma fração imprópria: primeiro vem a parte inteira, seguida da parte fracionária própria. Exemplos: 9 3/4, 3 2/5 e 6 1/2. Ele torna a leitura e a visualização de quantidade mais naturais em muitos contextos.
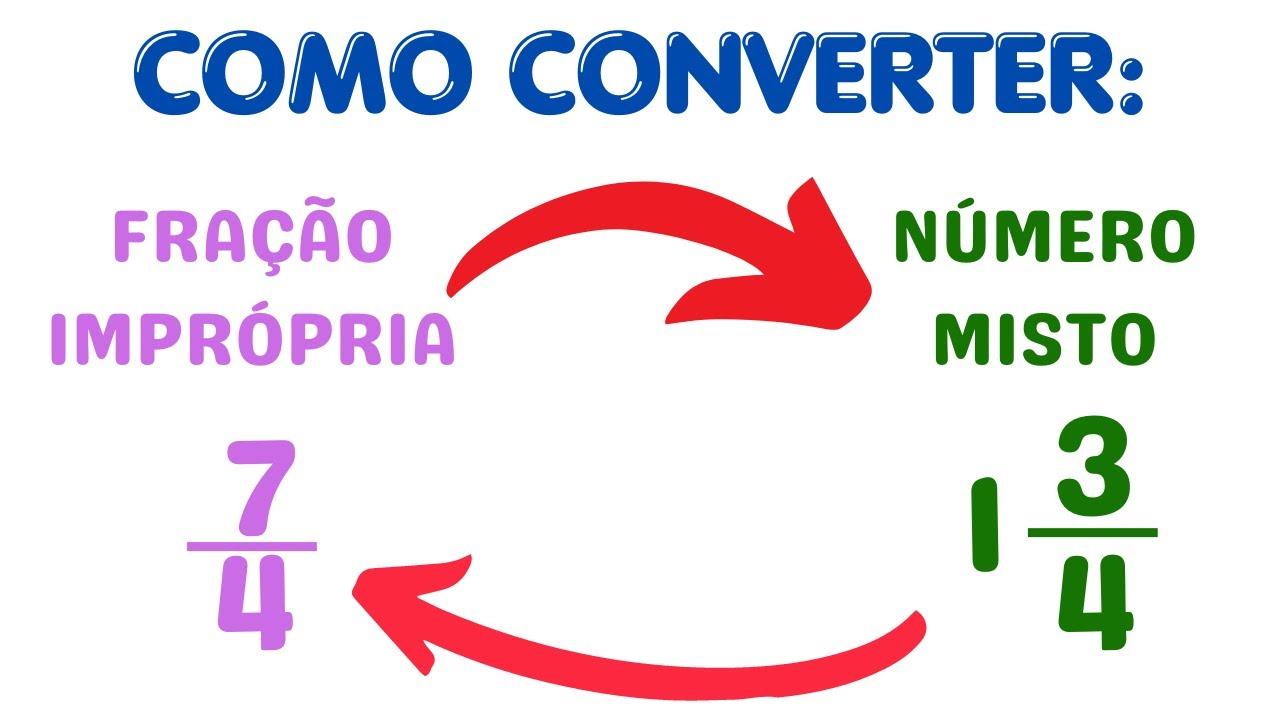
Como converter frações impróprias em frações próprias (via número misto)
Na prática, “converter uma fração imprópria em própria” significa separar a parte inteira e deixar a parte fracionária como uma fração própria. O método é simples: divida o numerador pelo denominador.
O procedimento segue três ideias: (1) o quociente inteiro vira a parte inteira (quantas unidades cabem inteiras), (2) o resto vira o novo numerador da parte fracionária e (3) o denominador permanece o mesmo. Assim, a parte fracionária resultante é sempre própria.
Exemplo prático com 13/5: 13 ÷ 5 = 2, com resto 3. Portanto, a escrita como número misto é 2 3/5. Repare que 3/5 é própria (3 < 5), e o 2 representa as duas unidades inteiras contidas em 13/5.
Outro exemplo útil: para 47/9, 47 ÷ 9 = 5, resto 2. Então, a forma mista é 5 2/9. Mais uma vez, a parte fracionária (2/9) é própria, e o 5 indica as cinco unidades completas existentes na fração original.
Em resumo deste bloco: dividir, anotar o quociente como inteiro, usar o resto como numerador e manter o denominador — isso transforma qualquer fração imprópria em um número misto cuja parte fracionária é uma fração própria.
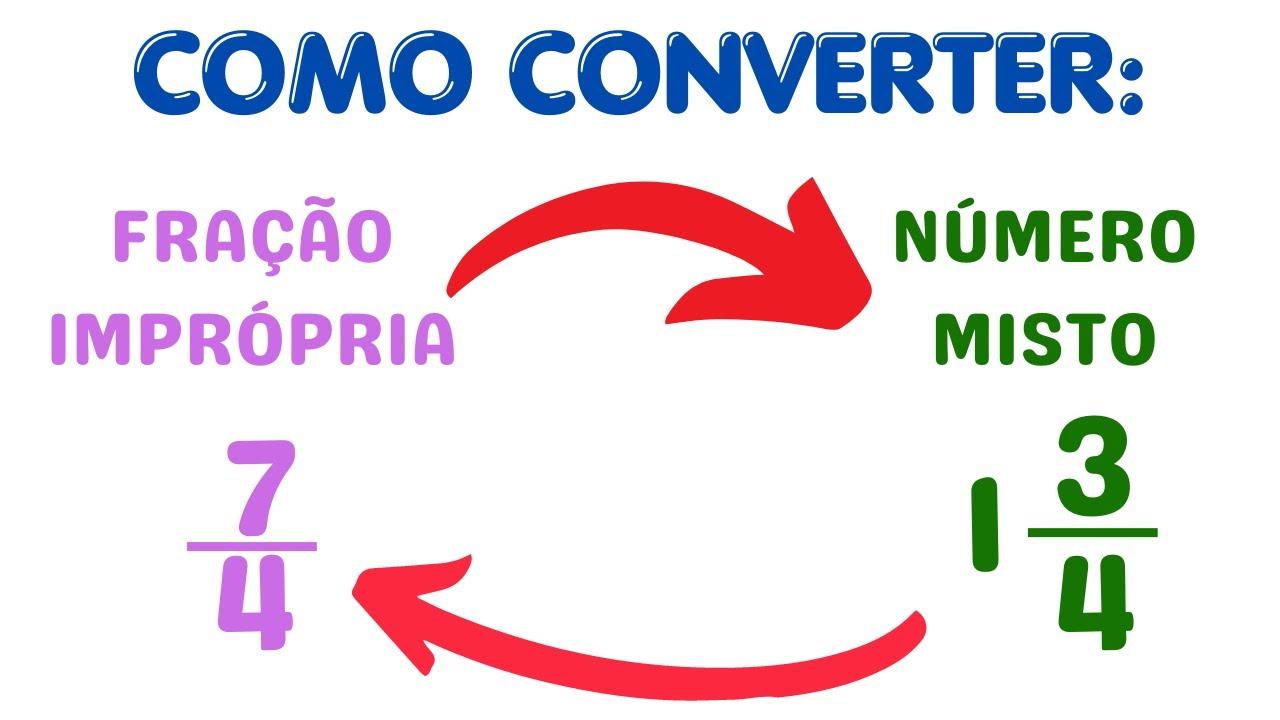
Conversão de fração mista em fração imprópria
Para ir no sentido oposto, some a parte inteira à fração convertendo a parte inteira para o mesmo denominador. No caso de 5 2/9, pense em 5 como 45/9 e então some 45/9 + 2/9 = 47/9.
Você também pode usar a “regra do produto e soma”: inteiro × denominador + numerador vira o novo numerador, e o denominador se mantém. Para 5 2/9, fica (5 × 9 + 2)/9 = 47/9, que coincide com o resultado acima.
Operações com frações impróprias no dia a dia
Frações impróprias aparecem com frequência quando somamos ou subtraímos frações; após calcular o resultado, é comum que ele saia impróprio e só então seja reescrito como número misto. Isso deixa o valor mais “legível” conforme o contexto.
Na adição, busque o denominador comum (geralmente o MMC). Exemplo: 5/3 + 7/4. O MMC de 3 e 4 é 12, então 5/3 = 20/12 e 7/4 = 21/12. Somando numeradores: 20 + 21 = 41, logo 41/12 é o resultado — ainda impróprio; para praticar, veja problemas de soma racional.
Na subtração, o raciocínio é idêntico: 5/3 − 3/2. O MMC de 3 e 2 é 6, então 5/3 = 10/6 e 3/2 = 9/6. Subtraindo numeradores: 10 − 9 = 1, resultando em 1/6 (agora própria).
Para multiplicar, multiplique numerador por numerador e denominador por denominador. Com 5/3 × 2/3, temos (5 × 2)/(3 × 3) = 10/9, que é uma fração imprópria (pode virar 1 1/9, se preferir mista).
Na divisão, multiplica-se pela inversa: (5/3) ÷ (2/3) = (5/3) × (3/2) = 15/6, que simplifica para 5/2. Se quiser mista: 2 1/2.
Aplicações: por que isso importa tanto
No mundo real, frações impróprias são essenciais em medições, proporções e escalas. Em receitas, por exemplo, 3/2 de xícara indicam 1 xícara cheia e mais meia — 1 1/2. Em construção, 7/4 m traduz 1 3/4 m, o que facilita a leitura em plantas e cortes.
Na Matemática escolar e universitária, essas frações são onipresentes em equações algébricas, simplificação de expressões e resolução de problemas. Ao converter para número misto, muitas vezes a interpretação fica mais clara, embora certos cálculos fiquem mais diretos mantendo a forma imprópria.
Em Física e Engenharia, valores fracionários acima da unidade aparecem em relações de grandeza, constantes e médias, e a forma imprópria evita ambiguidades em transformações e fórmulas.
Em Estatística, médias e razões podem surgir como frações impróprias, e saber passar para frações próprias (via número misto) ajuda na comunicação dos resultados, principalmente em relatórios e apresentações.
De modo geral, frações impróprias criam uma ponte natural para números mistos e decimais, favorecendo tanto a interpretação concreta quanto os procedimentos de cálculo.
História em poucas linhas e nomes influentes
Registros mostram que civilizações antigas já lidavam com partes de um todo em medições e comércio. Os egípcios, por exemplo, registravam quantidades fracionárias em seus métodos, ainda que com um sistema próprio e diferente do atual.
Com o avanço dos estudos, matemáticos árabes e europeus na Idade Média consolidaram a notação fracionária que usamos hoje. Al-Khwarizmi e Fibonacci (e também Nicolas Oresme) são frequentemente lembrados por popularizar e organizar ideias fundamentais, com obras como o Liber Abaci contribuindo para difundir a aritmética de frações.
No ensino moderno, frações impróprias fazem parte do currículo básico, e recursos digitais — jogos, softwares e conteúdos interativos — têm ajudado a tornar a visualização mais intuitiva e amigável.
Exercícios resolvidos
Exercício 1 — Simplificação: torne 18/36 uma fração irredutível. Como 18 e 36 são divisíveis por 18, resulta 1/2. Entre alternativas típicas, a correta seria 1/2.
Exercício 2 — Classificação: 28/18 é que tipo de fração? Como o numerador é maior que o denominador, trata-se de uma fração imprópria. Além disso, 28 e 18 são divisíveis por 2 (logo, não é irredutível) e 28 ÷ 18 não é inteiro exato (portanto, não é aparente).
Guia rápido: conversões essenciais com exemplos
Para transformar fração imprópria em número misto: divida o numerador pelo denominador, use o quociente como parte inteira e o resto como numerador da parte fracionária (denominador se mantém). Ex.: 13/5 → 2 3/5; 47/9 → 5 2/9.
Para escrever número misto como fração imprópria: converta o inteiro para o mesmo denominador e some. Ex.: 5 2/9 → 45/9 + 2/9 = 47/9. Alternativa: inteiro × denominador + numerador; tudo sobre o mesmo denominador.
Ao somar ou subtrair, encontre denominadores comuns (MMC) para reescrever as frações e só então efetue a operação. Multiplicações e divisões seguem regras diretas (produto dos numeradores/denominadores e multiplicação pela inversa, respectivamente).
Glossário essencial
Frações impróprias: frações com numerador maior ou igual ao denominador; valor ≥ 1.
Numerador: o “de cima” — quantidade de partes consideradas.
Denominador: o “de baixo” — em quantas partes iguais o todo foi dividido.
Frações próprias: numerador menor que o denominador; valor < 1.
Números mistos: combinação de parte inteira com uma parte fracionária própria.
Soma de frações: exige denominador comum (muitas vezes, o MMC) para somar numeradores.
Subtração de frações: espelho da soma — padronize denominadores e subtraia numeradores.
Multiplicação de frações: numerador × numerador e denominador × denominador.
Divisão de frações: multiplique a primeira fração pelo inverso da segunda.
Mínimo múltiplo comum (MMC): menor número múltiplo comum de dois ou mais denominadores.
Conversão: processo de passar de fração imprópria para número misto (e vice-versa), mantendo equivalência.
Proporções: relações entre grandezas, frequentemente expressas por frações.
Medidas: quantidades fracionárias comuns em receitas, construções e escalas.
Equações algébricas: expressões que podem conter frações impróprias e se beneficiam de conversões.
História das frações: evolução do conceito desde civilizações antigas até a padronização moderna.
Matemáticos notáveis: Al-Khwarizmi e Fibonacci, entre outros, contribuíram para a linguagem das frações.
Dominar as conversões entre impróprias, próprias (na parte fracionária do número misto) e mistas abre caminho para resolver problemas com mais confiança, clareza e eficiência, tanto na escola quanto nas aplicações reais — das panelas à bancada do laboratório.