- Ensinar frações com materiais manipuláveis facilita a compreensão de diferentes significados de fração e aproxima o conteúdo das vivências dos alunos.
- A BNCC recomenda o uso de representações concretas, pictóricas e simbólicas, favorecendo a articulação entre registros, como propõe a teoria de Duval.
- Pesquisas de autores como Nunes, Bryant, Magina, Campos e Merlini mostram que dificuldades em frações decorrem da ênfase em regras, e não em significados.
- O professor, ao planejar atividades com materiais reutilizáveis e comerciais, atua como mediador que promove conversões entre registros e discussões ricas em sala de aula.

Ensinar frações básicas com materiais manipuláveis é uma das formas mais eficazes de fazer com que crianças se apropriem desse conteúdo, que historicamente aparece nas pesquisas como um dos temas mais difíceis da matemática escolar. Quando o estudante pode tocar, recortar, comparar pedaços e discutir o que está vendo, a fração deixa de ser um número “estranho” escrito com numerador e denominador e passa a ter sentido no cotidiano.
Pesquisadores como Nunes, Bryant, Magina, Campos, Merlini, Duval, Vergnaud, Lorenzato e muitos outros têm mostrado que o entendimento de frações envolve vários significados, registros de representação e situações-problema. Além disso, a Base Nacional Comum Curricular (BNCC) orienta que o trabalho com números racionais, incluindo frações, comece cedo, em contextos significativos, conectados à vida real do aluno, com forte uso de materiais, jogos, registros gráficos e linguagem oral e escrita.
Fundamentos teóricos para ensinar frações com materiais manipuláveis

Para planejar boas atividades de frações com materiais manipuláveis, é essencial compreender os diferentes significados que a fração pode assumir, algo amplamente discutido em pesquisas como as de Vera Merlini e de Sandra Magina e Tânia Campos. Esses estudos mostram que muitos erros dos alunos não vêm de “falta de atenção”, mas do fato de que eles conhecem apenas um ou dois significados de fração, geralmente o de parte-todo, e têm pouca oportunidade de explorar os demais.
Merlini analisa em profundidade como estudantes de 5ª e 6ª séries (atual Ensino Fundamental Anos Finais) interpretam as frações em diferentes contextos, investigando se compreendem fração como parte de um todo, razão, operador, quociente e medida. Os resultados evidenciam que, quando o ensino se restringe a “pintar pedaços de pizza”, o aluno fica preso a um único tipo de situação e tem enorme dificuldade para resolver problemas mais complexos, como comparar frações em retas numéricas ou interpretar expressões do tipo 3/4 de 20.
Os trabalhos de Magina e Campos analisam a visão de professores e alunos sobre frações nos primeiros ciclos do Ensino Fundamental e mostram que muitos docentes também tiveram uma formação muito centrada em exercícios mecânicos, o que faz com que repliquem essa abordagem com seus estudantes. A pesquisa indica a necessidade de ampliar o repertório de significados e de estratégias didáticas, incluindo de forma sistemática o uso de materiais manipuláveis, jogos, problemas contextualizados e discussão coletiva das soluções.
Nunes e Bryant, em seus estudos sobre “crianças fazendo matemática”, reforçam que a construção do conhecimento numérico acontece muito além do ambiente escolar. Crianças resolvem situações de partilha, comparação de quantidades e raciocínios multiplicativos em contextos como feiras, brincadeiras, cozinha, vendas informais etc., o que se conecta com a famosa obra de Nunes, Carraher e Schliemann, “Na vida dez, na escola zero”. Essa pesquisa evidencia a diferença entre cálculos informais e tarefas escolares descontextualizadas.
Essa distância entre o raciocínio cotidiano e o escolar indica que o ensino de frações precisa aproveitar os conhecimentos informais dos estudantes, organizando-os e explicitando-os com a ajuda de materiais manipuláveis, linguagem oral, registros gráficos e simbólicos. Frações aparecem na partilha de bolo, no desconto de preços, na receita culinária, na medição de tempo e comprimento, e é papel do professor aproximar essas vivências da matemática formal.
Do ponto de vista da teoria dos registros de representação semiótica de Raymond Duval, compreender frações supõe transitar entre diferentes modos de representação: materiais físicos (como tiras de papel, tampinhas, tampas de garrafa), representações icônicas (desenhos, diagramas), registros gráficos (reta numérica, diagramas de área), linguagem natural (explicações orais e escritas) e registro simbólico (a escrita 3/5, por exemplo). O ponto-chave é a conversão entre registros, que aprofunda o entendimento.
Duval argumenta que muitos obstáculos cognitivos em matemática surgem justamente quando o aluno é exposto apenas a um tipo de registro, como a manipulação simbólica, sem ter oportunidade de relacionar esse registro a outros. No caso das frações, se o estudante só vê exercícios do tipo “calcule 2/3 + 1/3”, ele pode até memorizar o procedimento, mas não compreende o que está acontecendo com as quantidades envolvidas. Materiais manipuláveis atuam como registro de apoio para a construção de significado.
Frações na BNCC e o papel dos materiais manipuláveis
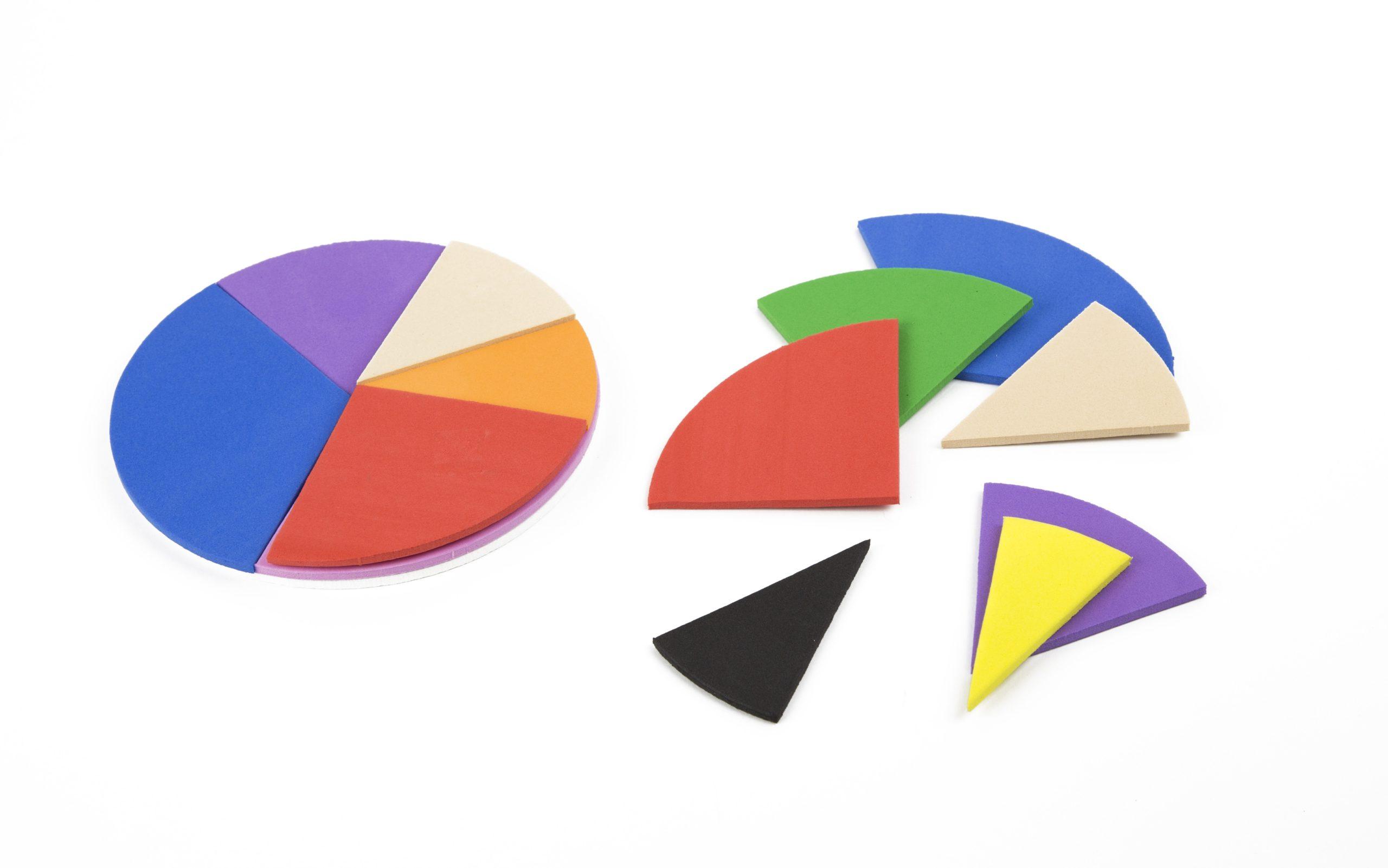
A Base Nacional Comum Curricular (BNCC), documento orientador da educação básica brasileira, destaca que o ensino de números racionais, incluindo frações, deve começar de forma gradual e significativa, especialmente a partir dos Anos Iniciais, por meio de situações que façam sentido para as crianças. O texto enfatiza que é fundamental trabalhar representações concretas e pictóricas antes de algoritmos e procedimentos formais.
Na BNCC, frações aparecem ligadas a diversas habilidades que envolvem tanto o uso de materiais concretos quanto a passagem para registros gráficos e simbólicos. Entre essas habilidades, destacam-se: compreensão de fração como parte de um todo, comparação e ordenação, uso da reta numérica e resolução de problemas em contextos do cotidiano.
A BNCC também incentiva o trabalho com significados variados de fração, embora muitas vezes isso fique implícito nas habilidades. Quando o documento menciona “partilhar igualmente”, “quantidade de uma grandeza em relação a outra”, “dobro, metade, terça parte” e “porcentagens”, está justamente abrindo espaço para explorar fração como quociente, operador, medida e razão. Cabe ao professor transformar essas indicações em situações concretas de sala de aula.
O uso de materiais manipuláveis está totalmente alinhado às diretrizes da BNCC para o Ensino Fundamental, principalmente porque favorece a resolução de problemas, a argumentação, o trabalho colaborativo e a construção de significados. Ao manipular objetos, os alunos podem experimentar, errar, tentar de outro jeito e discutir suas ideias com os colegas, o que reforça o caráter investigativo do aprender matemática.
Além disso, a BNCC valoriza a integração entre diferentes campos da matemática. Trabalhar frações com materiais manipuláveis permite conectar números, álgebra, grandezas e medidas e até estatística, por exemplo, quando os estudantes comparam partes de um conjunto, constroem gráficos a partir de frações ou discutem probabilidades simples em jogos. Assim, o ensino ganha vida em projetos e sequências didáticas, não ficando engessado em listas de exercícios.
Por que frações são tão difíceis para os alunos?

Diversas pesquisas brasileiras e internacionais, como as de Magina, Campos, Merlini, Nunes, Bryant e Vergnaud, apontam que frações são um dos tópicos de maior dificuldade para estudantes do Ensino Fundamental. Os erros mais comuns vão desde confundir numerador e denominador até achar que 1/8 é maior que 1/5 porque 8 é maior que 5. Entender de onde vêm esses erros ajuda o professor a planejar estratégias mais eficientes.
Um dos motivos para a dificuldade é que frações rompem com a lógica dos números naturais e com conceitos associados aos números reais. Nos naturais, quanto maior o número, maior a quantidade; nos racionais, isso nem sempre é verdade. Além disso, frações podem representar tanto uma quantidade menor que 1 quanto maior que 1, podem ser equivalentes e podem estar associadas a diferentes grandezas. Essas características exigem uma mudança de raciocínio.
Vergnaud, ao discutir as estruturas multiplicativas, mostra que muitos problemas de frações estão conectados à compreensão de razão e proporção, não apenas à ideia de “dividir em partes iguais”. Situações como “em uma sala, 3 de cada 5 alunos usam óculos” ou “a cada 2 copos de suco, adicionam-se 3 copos de água” exigem um pensamento multiplicativo e relacional. Esse tipo de raciocínio costuma ser pouco explorado em aulas tradiconais.
Outro fator de dificuldade, apontado por Nunes, Carraher e Schliemann, é a distância entre o que a criança consegue fazer fora da escola e o que é pedido em sala de aula. Um estudante pode repartir um bolo em porções iguais na prática, mas travar ao ver a mesma situação escrita em forma de problema. O desafio é criar pontes entre os dois mundos.
Além disso, pesquisas com professores, como as de Magina e Campos, indicam que muitos docentes se sentem inseguros em relação aos próprios conhecimentos sobre frações. Essa insegurança impacta diretamente a maneira como o conteúdo é apresentado: tende-se a priorizar “regras” e “truques” em vez de trabalhar raciocínios, significados e conexões entre registros. Materiais manipuláveis ajudam o professor a revisitar conceitos de forma investigativa.
Significados fundamentais de fração e como representá-los
Para um ensino sólido de frações básicas, é importante que o professor planeje atividades que contemplem, pelo menos, quatro grandes significados de fração: parte-todo, quociente, operador e razão/medida. Cada um desses significados pode ser introduzido e aprofundado usando materiais manipuláveis e diferentes registros de representação.
No significado parte-todo, a fração representa partes de um todo dividido em partes iguais. Materiais como pizzas de papel, barras de chocolate de papel cartão, tiras retangulares, discos recortados, tampinhas ou blocos encaixados são excelentes para esse tipo de exploração. O aluno visualiza que 3/4 significa três partes iguais de um todo dividido em quatro.
Já no significado quociente, a fração aparece como resultado de uma divisão que nem sempre é exata em números naturais. Por exemplo, repartir 3 bolos igualmente entre 4 pessoas pode ser representado como 3:4 = 3/4. Materiais manipuláveis permitem a partilha concreta e ajudam a conectar a divisão à fração resultante.
No significado operador, a fração indica uma ação sobre uma quantidade, como em “3/4 de 20” ou “2/5 da turma”. Esse significado é essencial para articular frações com porcentagens, escalas e problemas envolvendo aumento ou redução de quantidades. Coleções de objetos auxiliam na seleção da fração de um conjunto e na generalização do procedimento.
Por fim, no significado de razão ou medida, a fração expressa a relação entre duas grandezas, como “a cada 3 copos de suco, usamos 2 de água” (2/3). Situações de receita culinária, misturas, escalas em mapas e gráficos são contextos ricos para trabalhar esse significado. Medidores e tiras de papel favorecem a compreensão da relação entre medidas.
A teoria de Duval destaca que, ao trabalhar esses significados, é crucial que o aluno estabeleça conexões entre representações concretas, pictóricas, verbais e simbólicas. Assim, uma mesma fração deve poder ser vista como pedaços de papel, setor de um círculo, ponto na reta numérica e expressão numérica. A variedade de registros fortalece a compreensão.
Materiais manipuláveis: tipos, funções e potencial didático
Materiais manipuláveis podem ser comerciais, artesanais ou reutilizáveis, e cada tipo tem seu papel na aprendizagem de frações. O importante é como o material é explorado pedagogicamente, as perguntas feitas pelo professor e as formas de registro e discussão adotadas.
Entre os materiais comerciais, destacam-se jogos de frações padronizados, como círculos fracionários, barras de frações, dominós de frações e blocos de encaixe. Esses recursos facilitam comparações como 1/2, 1/3, 1/4 etc., mas devem ser integrados a problemas e desafios, não usados apenas mecanicamente.
Materiais artesanais, construídos pelo próprio professor ou pelos alunos, têm um potencial enorme de engajamento. Pizzas de cartolina, faixas de papel dobradas, tiras de EVA, discos de papelão e cartões com frações escritas à mão permitem que a turma participe da concepção do material, o que já é uma oportunidade de aprender. A construção coletiva do recurso é, por si só, aprendizagem.
O uso de materiais reutilizáveis, como embalagens, tampas de garrafa, caixas de papelão e restos de EVA, foi explorado em relatos de experiência como o de Carlos Augusto Messias Campos. Trabalhar com itens que seriam descartados conecta o ensino à educação ambiental e mostra que a criatividade pode substituir altos investimentos.
Campos descreve atividades em que operações com frações são introduzidas a partir da manipulação de tiras e pedaços de materiais reutilizáveis, permitindo aos alunos ver, por exemplo, que somar 1/4 + 1/4 é juntar dois pedaços do mesmo tamanho e obter 2/4. Essas experiências evitam a apresentação das operações como regras prontas e ajudam a perceber equivalências concretas.
Estratégias práticas para ensinar frações básicas com materiais manipuláveis
Ao planejar uma sequência de ensino de frações básicas com materiais manipuláveis, é interessante combinar momentos de exploração livre, desafios orientados e sistematização coletiva. Sequências que articulam exploração e formalização são mais eficazes.
Uma primeira estratégia é iniciar com situações de partilha em que os alunos realmente precisam dividir algo: bolos de papel, barras de chocolate de cartolina, pizzas de papelão, folhas com figuras geométricas etc. O professor pode propor, por exemplo, “temos dois bolos para três pessoas, como podemos repartir igualmente?”. Essas situações aproximam a ideia de 2/3 de forma concreta.
Em seguida, é possível usar retas numéricas construídas com tiras de papel ou fios, marcando frações como pontos ao longo da reta. Essa abordagem ajuda a consolidar fração como número, não apenas como parte de figuras. Pregadores, etiquetas ou cartolinas permitem comparar posições na reta e discutir qual fração é maior ou menor.
Outra estratégia é trabalhar equivalência de frações com peças que possam ser sobrepostas, como tiras ou círculos recortados de forma padronizada. Os alunos podem verificar que duas peças de 1/4 cobrem exatamente uma peça de 1/2, e que três peças de 1/6 têm o mesmo tamanho que uma peça de 1/2. A manipulação apoia a compreensão de equivalência.
Para operações com frações, especialmente adição e subtração, materiais manipuláveis permitem que o estudante veja o que está acontecendo com as partes. Somar frações com o mesmo denominador usando tiras ou discos de mesmo tamanho é um bom começo. À medida que a compreensão avança, problemas de soma racional explora casos com denominadores diferentes construindo peças compatíveis.
Problemas de quociente, como “três pizzas para quatro pessoas”, “cinco barras para dois grupos” ou “quatro metros de fita para seis presentes”, ganham clareza quando os materiais são efetivamente repartidos. Ao cortar tiras de papel ou usar fios e barbantes, os alunos percebem que a divisão pode ser representada por frações. Essas atividades tornam as frações mais significativas.
Registros de representação semiótica e a importância das conversões
A teoria de Duval sobre registros de representação semiótica oferece uma lente poderosa para entender o papel dos materiais manipuláveis no ensino de frações. Segundo o autor, aprender matemática não é apenas manipular símbolos, mas coordenar diferentes registros de representação, como figural, gráfico, algébrico, numérico e verbal.
No caso das frações, materiais manipuláveis compõem um registro figural-concreto que pode ser articulado a representações icônicas (desenhos), gráficas (retas numéricas, diagramas), verbais (explicações orais e escritas) e simbólicas (a/b). Atividades que promovem conversões entre registros são mais efetivas.
Duval destaca que certas conversões são mais difíceis do que outras, como passar do registro figural para o simbólico ou do verbal para o algébrico. Por isso, o professor precisa planejar momentos em que essas passagens sejam feitas de forma guiada, com perguntas, comparações e discussões coletivas. Guiar as conversões é tarefa intencional do docente.
Outra contribuição importante de Duval é a ideia de que, muitas vezes, o aluno fica preso a um único registro, o que limita sua compreensão. Em frações, isso acontece quando o estudante só lida com enunciados escritos, sem apoio concreto ou visual, ou, ao contrário, quando manipula materiais, mas nunca é convidado a passar para o registro simbólico. Equilibrar explorar, representar e formalizar é essencial.
Integrar materiais manipuláveis ao trabalho com diferentes registros não significa abandonar cálculos e algoritmos, mas sim dar-lhes sentido. Depois de muitas experiências partilhando, comparando e somando pedaços de forma concreta, faz mais sentido discutir por que, ao somar 1/4 + 1/4, somamos numeradores e mantemos o denominador. A formalização torna-se síntese do trabalho prático.
O papel do professor e a formação para ensinar frações
As pesquisas de Magina, Campos, Nunes, Lorenzato e outros autores apontam que o sucesso do ensino de frações com materiais manipuláveis depende fortemente do papel do professor, tanto em termos de planejamento quanto de mediação em sala de aula. Não basta “entregar o material”: a mediação é crucial.
Lorenzato, ao discutir a formação de professores de matemática, destaca a importância de que os docentes vivenciem, em sua própria formação, experiências significativas com materiais concretos e registros variados. Quando o futuro professor experimenta o papel de aprendiz, ele antecipa dificuldades e potencialidades, o que melhora o planejamento das aulas.
O uso de materiais reutilizáveis, como mostra o relato de Campos, também contribui para desenvolver uma postura mais investigativa e criativa no professor. Em vez de depender apenas de kits prontos, o docente aprende a olhar para o entorno com um olhar pedagógico e envolver os alunos na construção coletiva dos recursos. Essa prática estimula inovação didática.
A formação continuada, seja em cursos, grupos de estudo ou comunidades de prática, é um espaço privilegiado para discutir experiências com frações, analisar registros de alunos, refletir sobre dificuldades recorrentes e conhecer pesquisas atualizadas na área de educação matemática. Esses espaços articulam teoria e prática.
Em sala de aula, o professor atua como mediador que ajuda os estudantes a fazerem conexões: entre o material manipulável e o desenho no caderno, entre a fala do colega e a expressão matemática, entre o problema do cotidiano e a representação na reta numérica. Esse papel exige escuta atenta e valorização das estratégias dos alunos, incentivando o erro como oportunidade de aprendizagem e uma postura investigativa permanente sobre o que os estudantes estão pensando.
Quando materiais manipuláveis, fundamentos teóricos e boas práticas de sala de aula se encontram, as frações deixam de ser um “bicho de sete cabeças” e passam a ser um campo rico para desenvolver pensamento multiplicativo, raciocínio proporcional, compreensão de medida e capacidade de argumentar matematicamente. Integrar a BNCC, autores como Duval, Nunes, Bryant, Magina, Campos, Merlini, Lorenzato e Vergnaud e o uso criativo de materiais simples ajuda o professor a construir caminhos mais acessíveis e significativos para seus alunos se apropriarem das frações básicas.
