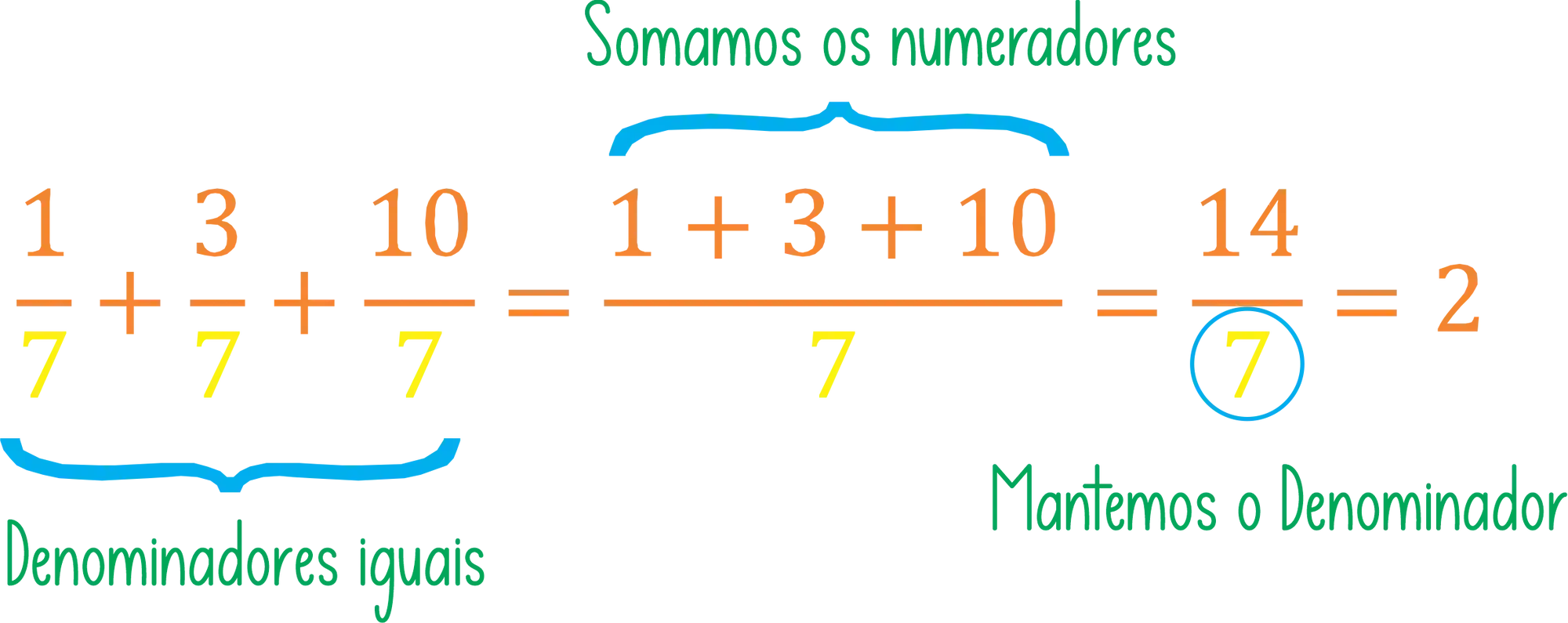- Denominadores iguais: some ou subtraia numeradores e mantenha o denominador.
- Denominadores diferentes: use MMC ou o produto dos denominadores e simplifique.
- Método borboleta agiliza adição e subtração em duas frações.
- Simplificar e converter frações impróprias em mistas melhora a leitura do resultado.

Quando falamos em somar frações, a primeira coisa que precisamos observar é se os denominadores são iguais ou diferentes. Isso determina o caminho a seguir: somar numeradores diretamente quando a base é a mesma, ou igualar denominadores quando são distintos. Não tem mistério, mas é importante dominar alguns truques sobre frações parciais para ganhar agilidade.
Neste guia, você vai ver de forma clara como proceder em cada caso, com o apoio do MMC (mínimo múltiplo comum), do chamado método prático (borboleta) e de exemplos resolvidos e problemas de soma racional passo a passo. Também abordaremos subtração de frações e operações com frações mistas, além de exercícios comentados para fixar o conteúdo.
O que é uma fração e por que o denominador importa?
Frações representam partes de um todo e fazem parte dos números racionais, podendo ser visualizadas em situações do dia a dia, como quando dividimos uma pizza. Se uma pizza é cortada em 8 partes iguais, cada fatia corresponde a 1/8. Se você comer 3 dessas fatias, terá consumido 3/8 da pizza.
Nem sempre, porém, os cortes são iguais entre diferentes situações. Às vezes, duas frações representam pedaços de tamanhos distintos (por exemplo, 1/4 e 1/6). Nesses casos, para somar ou subtrair, precisamos “trazer” as frações para um denominador comum, como mostram exemplos e exercícios, garantindo que estamos comparando quantidades da mesma base.
Em suma, o numerador indica quantas partes estamos considerando, enquanto o denominador mostra em quantas partes iguais o todo foi dividido. O denominador é a peça-chave para decidir o método de cálculo.
Soma de frações com denominadores iguais
Quando os denominadores já são iguais, o processo é direto: somamos apenas os numeradores e mantemos o denominador. É a situação mais simples.
Exemplos práticos:
• 2/8 + 3/8 = (2 + 3)/8 = 5/8.
• 2/5 + 2/5 = (2 + 2)/5 = 4/5.
Visualmente, pense novamente na pizza em 8 partes. Juntar 2 fatias com outras 3 fatias resulta em 5 fatias, sempre de oitavos. Não alteramos a “espessura” da fatia (o denominador), apenas contamos quantas fatias no total.
Soma de frações com denominadores diferentes usando MMC
Quando os denominadores são distintos, o caminho mais comum é usar o MMC (mínimo múltiplo comum). Esse número é o menor múltiplo que os dois (ou mais) denominadores compartilham. Convertendo as frações para denominadores iguais via MMC, podemos somar os numeradores com segurança.
Passos gerais:
1) Encontre o MMC dos denominadores.
2) Reescreva cada fração como equivalente com o denominador igual ao MMC.
3) Some os numeradores e mantenha o denominador comum.
4) Simplifique, se possível.
Exemplo 1 (duas frações): 1/2 + 2/3.
• MMC(2, 3) = 6.
• 1/2 = (1×3)/(2×3) = 3/6 e 2/3 = (2×2)/(3×2) = 4/6.
• 3/6 + 4/6 = 7/6 (fração imprópria). Se quiser, converta 7/6 em misto: 1 e 1/6.
Exemplo 2 (duas frações): 2/3 + 4/8.
• MMC(3, 8) = 24.
• 2/3 = (2×8)/(3×8) = 16/24 e 4/8 = (4×3)/(8×3) = 12/24.
• 16/24 + 12/24 = 28/24, que simplifica dividindo por 4: 7/6.
Exemplo 3 (três frações): 1/2 + 1/4 + 1/6.
• MMC(2, 4, 6) = 12.
• 1/2 = 6/12, 1/4 = 3/12, 1/6 = 2/12.
• 6/12 + 3/12 + 2/12 = 11/12. Note como o MMC elimina a confusão dos diferentes tamanhos de “fatia”.
Outra forma de pensar no procedimento com MMC é usar a “regra da equivalência”: dividimos o MMC pelo denominador original para descobrir por quanto multiplicar o numerador e o denominador daquela fração. Isso garante frações equivalentes com o denominador comum.
Alternativa: multiplicar os denominadores
Quando trabalhamos com duas frações, outra estratégia é usar como denominador comum o produto dos denominadores. Embora nem sempre seja o menor denominador possível, funciona e é simples de aplicar.
Exemplo: 1/2 + 2/3 com o produto dos denominadores.
• Denominador comum: 2×3 = 6 (neste caso, coincidiu com o MMC).
• Reescrevendo: 1/2 = 3/6 e 2/3 = 4/6.
• Soma: 3/6 + 4/6 = 7/6.
Para denominadores maiores, a fração intermediária pode ficar “grande”, mas a simplificação final recupera o valor correto.
Em somas com três ou mais frações, multiplicar todos os denominadores deixa o cálculo rápido de obter o denominador comum, porém pode gerar números maiores. Usar MMC tende a criar contas menores e facilitar a simplificação.
Método prático (borboleta) para a adição
O método da “borboleta” é um atalho visual muito usado para somar duas frações a/b e c/d. Basta multiplicar cruzado para obter o novo numerador e multiplicar os denominadores para obter o novo denominador:
• a/b + c/d = (a×d + b×c) / (b×d).
Exemplos:
• 3/7 + 4/5 = (3×5 + 7×4) / (7×5) = (15 + 28)/35 = 43/35.
• 2/5 + 4/9 = (2×9 + 5×4) / (5×9) = (18 + 20)/45 = 38/45.
É rápido, funciona bem com duas frações e leva direto ao denominador comum (o produto).
Subtração de frações: iguais e diferentes
Subtrair frações segue a mesma lógica da adição, trocando a soma pela diferença. Se os denominadores forem iguais, subtraia apenas os numeradores e mantenha a base.
Exemplos com denominadores iguais:
• 5/8 − 2/8 = (5 − 2)/8 = 3/8.
• 3/5 − 2/5 = (3 − 2)/5 = 1/5.
Para denominadores diferentes, igualamos os denominadores (usando MMC ou o produto dos denominadores) e então subtraímos os numeradores. Depois, simplifique quando possível.
Exemplos com denominadores diferentes:
• 3/4 − 2/3: MMC(4, 3) = 12 → 9/12 − 8/12 = 1/12.
• 2/3 − 4/8: MMC(3, 8) = 24 → 16/24 − 12/24 = 4/24 = 1/6.
Método borboleta para subtração (duas frações):
• a/b − c/d = (a×d − b×c) / (b×d).
Exemplos:
• 5/7 − 3/5 = (5×5 − 7×3) / 35 = (25 − 21)/35 = 4/35.
• 3/5 − 4/9 = (3×9 − 5×4) / 45 = (27 − 20)/45 = 7/45. Se a diferença no numerador ficar negativa, o resultado é uma fração negativa.
Frações mistas: soma e subtração
Frações mistas têm uma parte inteira e uma parte fracionária (por exemplo, 2 1/3). Para operar com mistas, há dois caminhos: somar/subtrair primeiro as partes inteiras e depois as frações, ou converter tudo para frações impróprias e, ao final, reconverter.
Exemplo de soma direta por partes:
2 1/3 + 3 2/5 = (2 + 3) + (1/3 + 2/5) = 5 + (5/15 + 6/15) = 5 + 11/15 = 5 11/15. Ajustar as frações com MMC facilita a parte fracionária.
Exemplo de subtração direta por partes:
4 1/2 − 3 2/5 = (4 − 3) + (1/2 − 2/5) = 1 + (5/10 − 4/10) = 1 + 1/10 = 1 1/10. Se a parte fracionária “ficar negativa”, é possível fazer um empréstimo da parte inteira.
Se preferir, converta para impróprias:
• 2 1/3 = 7/3 e 3 2/5 = 17/5. Some usando MMC ou borboleta, e depois reconverta para mista. Esse método padroniza o processo quando há muitas mistas envolvidas.
Exercícios resolvidos e situações do cotidiano
Exercício 1 (adição com mesmo denominador): Um bolo foi dividido em 12 pedaços iguais. João comeu 3/12 e Maria comeu 4/12. Quanto foi consumido no total?
Alternativas: (A) 4/12 (B) 5/12 (C) 6/12 (D) 7/12 (E) 8/12.
Solução: 3/12 + 4/12 = 7/12 → alternativa D. Denominadores iguais pedem apenas a soma dos numeradores.
Exercício 2 (subtração com denominadores diferentes): Agnaldo tinha 2/5 de uma pizza; seu irmão comeu 1/8 dela. Quanto restou para Agnaldo?
Resolução: 2/5 − 1/8. MMC(5, 8) = 40 → 16/40 − 5/40 = 11/40 → alternativa correta: 11/40. Encontrar o denominador comum é a chave.
Exercício 3 (adição com MMC explicado por fatoração): Some 3/8 e 9/20.
• MMC(8, 20) = 40 (pois 8 = 2³ e 20 = 2²×5; logo MMC = 2³×5 = 40).
• 3/8 = (3×5)/(8×5) = 15/40 e 9/20 = (9×2)/(20×2) = 18/40.
• Soma: 15/40 + 18/40 = 33/40. Quando já está irredutível, não há simplificação possível.
Exercício 4 (adição e subtração em situação concreta): Comprei uma barra com 8 quadradinhos. Comi 3 ontem e 2 hoje. Que fração comi? E quanto falta?
• Fração comida: 3/8 + 2/8 = 5/8.
• Fração que falta: 8/8 − 5/8 = 3/8. Problemas do cotidiano ajudam a fixar o raciocínio.
Exercício 5 (proporção de ingredientes): Ana tem 6 ovos. Usará metade para um bolo e um terço para uma omelete. Quantos ovos usará no total?
• Metade de 6 = 3 ovos; um terço de 6 = 2 ovos → 3 + 2 = 5 ovos. (Opções típicas: a) 4 ovos b) 5 ovos c) 6 ovos). Quando a referência é um número inteiro, calcule as frações sobre o total.
Dicas práticas, simplificação e erros comuns
Simplifique sempre que possível. Se numerador e denominador têm um divisor comum, divida ambos pelo mesmo número (por exemplo, 28/24 → divide por 4 → 7/6). Isso deixa a fração mais “limpa”.
Prefira o MMC quando os denominadores são altos ou pouco “amigáveis”. O MMC dá o menor denominador comum e costuma gerar números mais fáceis de manipular. Já o produto dos denominadores pode ser útil para ganhar rapidez, sabendo que a simplificação virá depois.
Evite confundir numerador e denominador. O numerador é a quantidade de partes; o denominador é em quantas partes iguais o todo foi dividido. Trocar essas posições muda completamente o valor.
No método borboleta, fique atento aos sinais na subtração. É (a×d − b×c) no numerador, não o contrário. Se o resultado do numerador for negativo, a fração é negativa.
Frações mistas exigem cuidado com “empréstimos” na subtração direta. Se a parte fracionária do minuendo é menor que a do subtraendo, transforme uma unidade inteira em fração equivalente para prosseguir. Alternativamente, converta tudo para frações impróprias antes de calcular.
Referências e materiais consultados
Parte do conteúdo e dos exemplos foi inspirado em materiais didáticos e em textos educacionais de matemática, incluindo explicações sobre soma com denominadores iguais e diferentes, uso do MMC e do método prático (borboleta). Entre as fontes consultadas estão obras de referência em matemática escolar e artigos educativos especializados.
• Referência didática: Dante, Luiz Roberto. Matemática: Contextos & Aplicações – Volume 1. São Paulo: Ática, 2011. Obra com abordagem sólida de operações com frações.
• Textos educacionais que discutem soma e subtração de frações, MMC e exemplos passo a passo em português. Conteúdo usado como base para reorganizar e reescrever as explicações deste guia.
• Materiais com exercícios e aplicações práticas sobre adição e subtração de frações, incluindo problemas de contexto, como divisão de alimentos e ingredientes de receitas. Esses exercícios reforçam o entendimento conceitual.
Neste passeio completo pelas frações, vimos como tratar casos com denominadores iguais e como igualá-los quando são diferentes, explorando o MMC, o produto dos denominadores e o método borboleta, além de subtrações, frações mistas e várias situações resolvidas. Com prática regular e atenção à simplificação, somar e subtrair frações vira uma habilidade automática e muito útil no dia a dia.