Sólidos da revolução: volume, tipos, exercícios resolvidos

Os sólidos da revolução são figuras geométricas tridimensionais obtidas a partir da rotação de uma região plana em torno de um eixo. Neste contexto, é possível determinar o volume desses sólidos através de integração e aplicação de fórmulas específicas para cada tipo de figura. Dentre os principais tipos de sólidos da revolução estão o cilindro, o cone e a esfera. Para compreender melhor o cálculo do volume desses sólidos, é importante praticar exercícios resolvidos que exemplifiquem a aplicação das fórmulas e conceitos envolvidos. Neste artigo, iremos explorar os diferentes tipos de sólidos da revolução, apresentar as fórmulas de cálculo de volume e resolver alguns exercícios práticos para facilitar o entendimento desse tema.

Descubra como determinar o volume de um sólido criado por uma rotação.

Para determinar o volume de um sólido criado por uma rotação, é necessário utilizar o conceito de sólidos da revolução. Esses sólidos são formados a partir da rotação de uma região plana em torno de um eixo. O volume desse sólido pode ser calculado utilizando integração e a fórmula apropriada para cada tipo de sólido.

Um dos tipos mais comuns de sólidos da revolução é o cilindro. Para determinar o volume de um cilindro, basta utilizar a fórmula V = πr^2h, onde r é o raio da base do cilindro e h é a altura do cilindro. Para um sólido mais complexo, como um cone ou uma esfera, é necessário adaptar a fórmula e considerar a geometria específica do sólido.

Para resolver exercícios envolvendo sólidos da revolução, é importante identificar o eixo de rotação, a região plana a ser rotacionada e a fórmula correta para o cálculo do volume. Ao integrar a função que descreve a área da seção transversal da região plana, é possível obter o volume do sólido gerado pela rotação.

Portanto, ao compreender os conceitos de sólidos da revolução e a aplicação da integração para o cálculo de volume, é possível determinar com precisão o volume de um sólido criado por uma rotação.

Conheça os tipos de sólidos criados por rotação de figuras geométricas.

Quando uma figura geométrica é rotacionada em torno de um eixo, é possível criar diversos tipos de sólidos da revolução. Esses sólidos possuem características únicas e podem ser encontrados em diferentes situações do cotidiano.

Um dos tipos mais comuns de sólidos da revolução é o cilindro, que é gerado a partir da rotação de um retângulo em torno de um de seus lados. O cilindro possui duas bases circulares e uma superfície lateral curva. Ele é muito utilizado em objetos do dia a dia, como latas de refrigerante e potes de sorvete.

Outro sólido importante é a esfera, que é obtida pela rotação de um círculo em torno de seu diâmetro. A esfera não possui faces, arestas ou vértices, sendo uma figura geométrica perfeita. Ela é comumente encontrada em bolas de diversos esportes, como futebol e basquete.

Além do cilindro e da esfera, existem também outros sólidos da revolução menos conhecidos, como o cone e o toro. O cone é gerado pela rotação de um triângulo em torno de um de seus lados, enquanto o toro é obtido pela rotação de um círculo em torno de um eixo exterior a ele.

Para calcular o volume desses sólidos, é necessário utilizar fórmulas específicas para cada tipo de figura. Por exemplo, o volume de um cilindro pode ser calculado utilizando a fórmula V = π*r^2*h, onde r é o raio da base e h é a altura do cilindro.

Para aprimorar seus conhecimentos sobre sólidos da revolução, é importante resolver exercícios que envolvam o cálculo de volumes e áreas dessas figuras. Praticar é essencial para fixar os conceitos e se tornar mais familiarizado com esses tipos de sólidos.

Conhecer os diferentes tipos de sólidos e suas características é fundamental para compreender a geometria espacial e aplicar esses conceitos em situações práticas do dia a dia.

Exemplos para calcular o volume de diferentes formas geométricas.

Para calcular o volume de diferentes formas geométricas, é importante conhecer as fórmulas específicas para cada tipo de sólido. Vamos ver alguns exemplos:

1. Cilindro:

Para calcular o volume de um cilindro, utilizamos a fórmula V = π * r² * h, onde r é o raio da base e h é a altura do cilindro. Por exemplo, se tivermos um cilindro com raio de 5cm e altura de 10cm, o volume será V = π * 5² * 10 = 250π cm³.

2. Esfera:

Para calcular o volume de uma esfera, usamos a fórmula V = 4/3 * π * r³, onde r é o raio da esfera. Por exemplo, se o raio da esfera for 3cm, o volume será V = 4/3 * π * 3³ = 36π cm³.

3. Cone:

Para calcular o volume de um cone, utilizamos a fórmula V = 1/3 * π * r² * h, onde r é o raio da base e h é a altura do cone. Por exemplo, se tivermos um cone com raio de 4cm e altura de 8cm, o volume será V = 1/3 * π * 4² * 8 = 128π cm³.

4. Cubo:

Para calcular o volume de um cubo, basta elevar o comprimento de um dos lados ao cubo. Portanto, se tivermos um cubo com lado de 6cm, o volume será V = 6³ = 216 cm³.

Com esses exemplos, fica mais fácil compreender como calcular o volume de diferentes formas geométricas. Pratique resolvendo exercícios de sólidos da revolução para aprimorar suas habilidades em geometria.

Descubra como determinar o volume de um objeto tridimensional utilizando fórmulas matemáticas simples.

Quando falamos em objetos tridimensionais, é importante saber como determinar o seu volume. Uma forma de fazer isso é através dos Sólidos da revolução, que são figuras formadas a partir da rotação de uma curva em torno de um eixo. Para calcular o volume desses objetos, podemos utilizar fórmulas matemáticas simples.

Uma das formas mais comuns de calcular o volume de um sólido da revolução é utilizando a fórmula do volume do cilindro. O volume do cilindro é dado pela fórmula V = π * r^2 * h, onde r é o raio da base do cilindro e h é a altura do cilindro. Ao aplicar essa fórmula, conseguimos determinar o volume de objetos como garrafas, latas e tubos.

Outra fórmula importante para calcular o volume de um sólido da revolução é a do volume da esfera. O volume da esfera é dado por V = 4/3 * π * r^3, onde r é o raio da esfera. Com essa fórmula, podemos determinar o volume de objetos esféricos, como bolas de gude e planetas.

Além disso, é possível utilizar a fórmula do volume do cone para determinar o volume de um sólido da revolução em forma cônica. O volume do cone é dado por V = 1/3 * π * r^2 * h, onde r é o raio da base do cone e h é a altura do cone. Com essa fórmula, conseguimos calcular o volume de objetos como cones de trânsito e chapéus de festa.

Para praticar o cálculo do volume de sólidos da revolução, é importante resolver exercícios que envolvam a aplicação dessas fórmulas. Dessa forma, é possível aprimorar a compreensão dos conceitos matemáticos e a habilidade de calcular volumes de objetos tridimensionais.

Praticar a resolução de exercícios é fundamental para aprimorar essas habilidades e garantir um entendimento sólido sobre o cálculo de volumes em geometria tridimensional.

Sólidos da revolução: volume, tipos, exercícios resolvidos

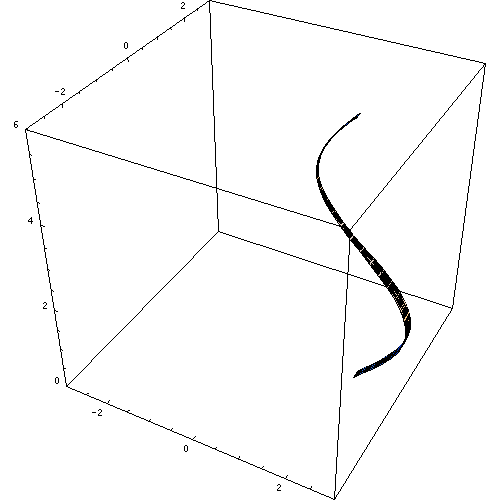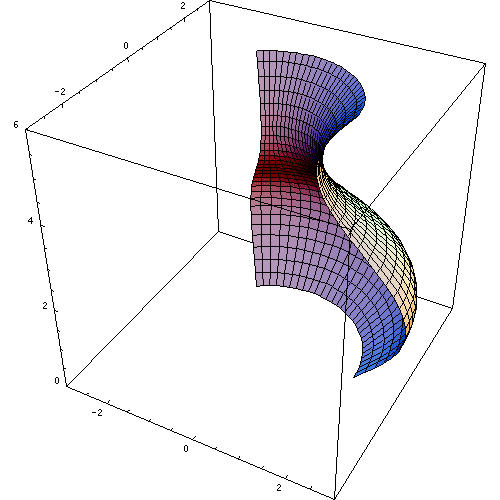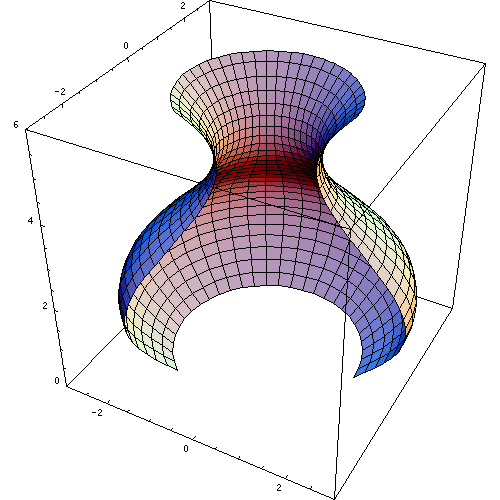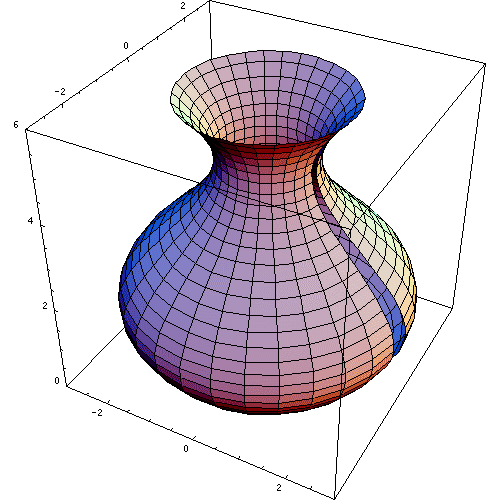
O sólido da revolução é a figura tridimensional gerada pela rotação de uma superfície plana em torno do eixo axial ou eixo de revolução. A Figura 1 mostra uma animação de um sólido de revolução gerado dessa maneira.

Outro exemplo muito fácil de visualizar é gerar um cilindro circular reto, girando um retângulo de altura ou comprimento he raio r, em torno do eixo x positivo (figura 2). Para encontrar seu volume, existe uma fórmula bem conhecida:

V = área base x altura

Outros sólidos da revolução são a esfera, o cone circular reto e várias figuras, dependendo da superfície girada e, é claro, do eixo selecionado.

Por exemplo, girar o semicírculo em torno de uma linha paralela ao diâmetro produz um sólido com uma revolução oca.

Para o cilindro, o cone, a esfera, sólida e oca, existem fórmulas para encontrar o volume, que depende do raio e da altura. Mas quando eles são gerados por outras superfícies, o volume é calculado usando integrais definidas.

Tipos de sólidos de revolução

Os sólidos da revolução podem ser classificados de acordo com a curva que os gera:

Esfera

Basta girar um semicírculo em torno de um eixo que será o diâmetro da esfera do raio R. Seu volume é:

_Esfera V = (4/3) πR ³

Cone

Para obter um cone de altura H e raio R, a superfície a ser rotacionada é um triângulo retângulo, em torno do eixo axial que passa por uma das pernas. Seu volume é:

_Cone V = (1/3) πHR ²

Cilindro

Girando um retângulo em torno de um eixo axial que passa por um dos lados, que pode ser o lado mais curto ou o mais longo, obtemos um cilindro circular reto de raio R e altura H, cujo volume é:

_Cilindro V = πR ² H

Toroid

O toróide tem a forma de um donut. É obtido girando uma região circular em torno de uma linha no plano que não cruza o círculo. Seu volume é dado por:

V _toróide = 2πa ² R

Onde a é o raio da seção transversal e R é o raio do toróide, de acordo com o esquema apresentado na figura:

Métodos para calcular o volume de um sólido de revolução

No cálculo integral, esses dois métodos são frequentes:

– Discos e arruelas

-Cartuchos

Método de disco ou arruela

Ao fatiar um sólido de revolução, a seção transversal pode ser um disco, se o sólido for sólido, ou pode ser uma espécie de arruela (um disco com um orifício no meio), se for um sólido oco.

Suponha que uma região plana seja girada em torno do eixo horizontal. A partir dessa região plana, pegamos um pequeno retângulo de largura Δx, que é girado perpendicularmente ao redor do eixo axial.

A altura do retângulo está entre a curva mais externa R (x) e a mais interna r (x). Eles correspondem ao raio externo e raio interno, respectivamente.

Fazer essa rotação gera uma arruela de volume ΔV, dada por:

ΔV = Volume total – volume do furo (se houver)

Lembrando que o volume de um cilindro circular reto é π. raio ² x altura, temos:

? V = π [R ² (x) – r ² (X)] Ax

O sólido pode ser dividido em uma infinidade de pequenas porções de volume ΔV. Se somarmos todos, teremos o volume total.

Para isso, fazemos o volume ΔV tender a 0, com o qual Δx também se torna muito pequeno, tornando-se um diferencial dx.

Portanto, temos uma integral:

V = ∫ _um ^b π [R ² (x) – r ² (X)] dx

Caso o sólido seja sólido, a função r (x) = 0, a fatia do sólido que é gerado é um disco e o volume permanece:

V = ∫ _a ^b πR ² (x) dx

Quando o eixo de revolução é vertical, as equações acima assumem a forma:

V = ∫ _um ^b π [R ² (y) – r ² (Y)] dy y V = ∫ _um ^b πR ² (y) dy

Método de camadas

Como o nome indica, esse método envolve assumir que o sólido é composto de camadas de espessura diferencial. A camada é um tubo fino que se origina da rotação de um retângulo paralelo ao eixo de rotação.

Temos as seguintes dimensões:

-Altura do retângulo w

-O comprimento h

-A distância do centro do retângulo ao eixo de rotação p

Sabendo que o volume da camada é volume externo – volume interno :

π (p + p / 2) ² h – π (p – p / 2) ² h

Ao desenvolver produtos notáveis ​​e simplificar, você obtém:

Volume da camada = 2π⋅p⋅w⋅h

Agora vamos fazer a altura w do retângulo ser Δy, como visto na figura a seguir:

Com isso, o volume ΔV é:

ΔV = 2π pxhx Δy

E tornando o número de camadas n muito grande, Δy se torna um dy diferencial, com o qual o volume total é integral:

V = ∫ _c ^d 2π p (y) h (y) dy

O procedimento descrito é aplicado de maneira semelhante quando o eixo de revolução é vertical :

Exercício resolvido

Encontre o volume gerado pela rotação da região plana entre as curvas:

y = x ² ;  y = 0; x = 2

Em torno do eixo y.

Solução

-A primeira coisa que devemos fazer é representar graficamente a região que irá gerar o sólido da revolução e indicar o eixo de rotação. Temos isso no gráfico a seguir:

-Agora, estamos procurando as interseções entre a curva y = x ² e a linha x = 2. Por seu lado, a linha y = 0 não é outra senão o eixo x.

No gráfico, é fácil notar que a parábola e a linha se cruzam no ponto (2,4), o que é corroborado substituindo x = 2 em y = x ² .

-Em seguida, escolha um dos métodos para calcular o volume, por exemplo, o método de estratificação com eixo de rotação vertical:

V = ∫ _a ^b 2π p (x) h (x) dx

Etapa 1: desenhe o retângulo

Importante: No método de camadas, o lado longo do retângulo é paralelo ao eixo de rotação.

Etapa 2: determinar p (x)

O raio da camada é x

Etapa 3: determinar h (x)

A altura do retângulo é determinada pela parábola x ² .

Etapa 4: estabelecer e resolver a integral do volume

A variável de integração é x, que varia entre 0 e 2, com isso temos os limites de integração. Substituindo expressões por p (x) eh (x)

Referências

1. Larson, R. 2010. Cálculo de uma variável. 9º. Edição. McGraw Hill.
2. Purcell, E. 2007. Cálculo com geometria analítica. 9º. Edição. Pearson Education.
3. Wikipedia. Sólido de revolução. Recuperado de: en.wikipedia.org.
4. Wikipedia. Toróide. Recuperado de: es.wikipedia.org.
5. Wolfram MathWorld. Sólido de revolução. Recuperado de: mathworld.wolfram.com.